
/// 注:本文虽然大篇幅讨论的虚构四维世界中的虚构的物理规律,但也对纯数学的单位四维2-向量的均匀随机分布规律进行了讨论。
内容概要
- 四维贾尼别科夫效应
- 有能量交换的多体旋转系统
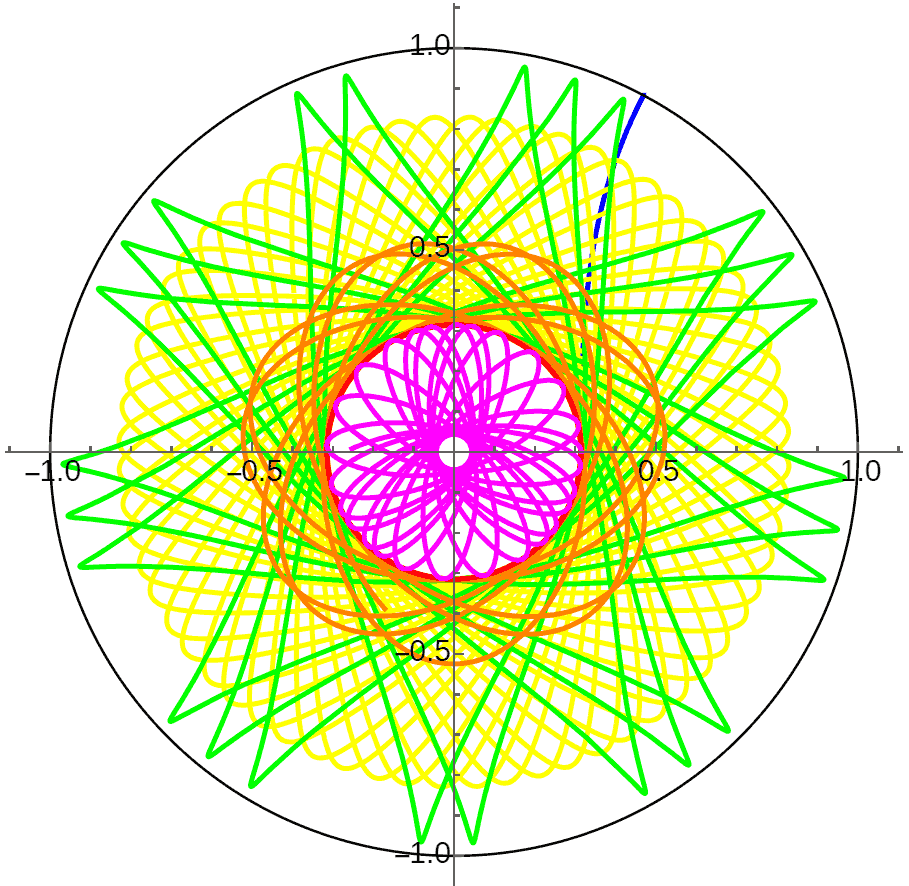
- 角动量的随机分布律
- 四维刚体的的主轴定理
贾尼别科夫效应
一个前苏联的宇航员在太空中把弄一个T字形零件,他偶然发现让零件漂浮着快速旋转起来,零件的旋转方向却突然时不时在空中翻转,后来就以他的名字(Джанибеков)命名了这个贾尼别科夫效应(Dzhanibekov Effect)。

这篇文章将介绍Tesserxel中的四维一维轨道火车(传统铁路+火车)、二维轨道火车(也叫汽火/火汽车)、无人机与四维客机四个示例场景的操控玩耍教程。之前几期介绍的场景都是静止的,我们只是主动操作摄像机换着四维角度以及三维角度观察场景本身或三维照片。这篇文章侧重于怎样驾驶操纵这些四维的交通工具,特别是如何操纵四维客机起降。这几个场景对应的交通工具的设计细节与运行原理已经在之前文章中均有一些介绍,感兴趣的话可以看看:
提示:如果在玩耍过程中觉得左边的示例场景侧栏很碍事可以点击顶部的隐藏侧栏,再设置浏览器进入全屏模式来获得最佳体验。


四维世界中的飞行器结构会是什么样的呢?这篇文章我们将来看看一些关于从四维风扇到无人机再到大型客机的可能设计思路。
在我多年前的旧文《双曲空间——数学艺术》中介绍了双曲空间这一数学几何概念,不久前《闵氏空间与常曲率空间》也再次提到了它。类似四维空间系列与四维世界系列,本文将讨论双曲空间世界中的一些有意思的物理现象。在这个blog上我花了大量笔墨介绍了一个想象之中的四维世界,同时也介绍了通过非欧几何构造出来的双曲空间的世界、p范数世界等,甚至还有反演地球、氧化剂还原剂星球等纯脑洞的世界……从这篇文章起专门开一个“奇特世界”系列来介绍一些除四维世界之外的脑洞想象。
由于前面第一篇文章主要在给读者形象展示双曲空间,后一篇文章又着重于将在闵氏空间中的构造方法,都没有系统认识双曲几何,因此我们先补充介绍一些之前没提到的几何性质,然后我们将基于此描述一个想象中的双曲宇宙,探讨里面的力学、天文学……
第一次看玩Tesserxel系列的话请先阅读上一篇文章了解Tesserxel四维场景的基本操作方法哦。这篇文章我们将挑几个场景来介绍,本文将依次介绍复杂旋转体、直积形以及四维高速公路场景。超球、球环、环球等基本几何体之前已经介绍很多了,理解了本文更复杂的场景后,那些简单几何体就留给读者去自由探索吧。

谷歌Chrome浏览器终于在113版本(至少我在windows下现在已经能自动更新到该版本了,但我发现113版有时会有物体过一会就消失不渲染的bug,后面的版本已修复)正式开始支持WebGPU了!这就意味着我的Tesserxel四维引擎项目可以直接在最新版的Chrome浏览器上直接运行了。我将开启一个Tesserxel玩耍教程系列,解释Tesserxel示例的场景。
玩Tesserxel首先得知道基本的四维空间概念,然后请阅读《四维世界(四):二维生物视觉》《四维世界(五):体验四维人的视觉与方向感》这两篇介绍四维生物视觉的文章,明白立体照片,截面与四维深度等概念。文章中的交互四维场景除了用的是上一代WebGl写的引擎,本质与Tesserxel的交互方式区别不大,只是快捷键略有调整,所以如果之前有玩过一些四维场景,上手Tesserxel是零难度的。注意,要想直观领略抽象的四维空间,除了要一块稍微好点的显卡,还需要尽可能多调动感官交互,因此Tesserxel没有考虑适配手机操作。由于很多操作与原来老引擎相同,这里就不再赘述摄像机移动旋转与简单的方向辨识了,这篇文章重点介绍三维体素照片渲染设置相关的操作,并罗列出常见相机控制方法。