//注:本文于2020年8月大幅改动并加入了大量新内容!
//注:本文于2023年1月修正了最后一小节关于引力轨道计算的错误并做了相应补充!
不一样的距离公式
大家知道勾股定理是直角边两边的平方和等于第三边,这是一个不用怀疑的事实,也有各种方法证明勾股定理,其中最著名的莫过“无字证明”了: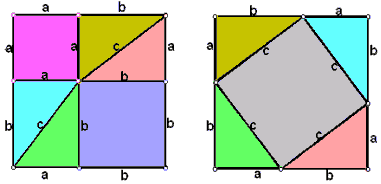
但其实这个证明是有问题的,因为勾股定理是可以不成立的!大家应该听说过非欧几里得几何吧,我前面的一篇文章也讲过一种“双曲几何”。非欧几里得几何本来是从否定平行公设出发推出的一系列新的几何学,但它们的实质是度量不一样,即计算距离的公式不一样。我们熟知的计算两点间距离的公式:$d=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$也是从勾股定理中来的。如果现在我们“强行”把距离规定成$d=\sqrt[p]{|x_2-x_1|^p+|y_2-y_1|^p}$,即勾股定律变成两边p次方和等于斜边p次方——这种空间我们称为p-范数空间。有一个很棒的短篇科幻小说叫《勾股》,讲述了一个受虫洞影响导致勾股定理中的幂从2偏离到2.013的故事,虽然广义相对论已经能证明弯曲时空勾股定理的次方数还是2,但这并不妨碍它是一篇很好的脑洞很大的小说。如果真实存在这种空间会怎样呢?下面我们就来探究奇妙的p范数空间。
首先是“圆”变了。圆的定义是平面上到定点等距的点的集合,距离定义变了图形就变了,圆周率(周长除以直径)也就变了(当然这里的“周长”要用新定义的距离公式计算)。可能最近比较著名的应该属小米的新logo设计了——它的外框曲线是3-范数下的圆,就这个东西价值200万元。
说到圆我们就要说旋转的概念。世界上最完美的图形就是圆。但现在我们不敢这样说了。在3范数(p=3)的世界里,曲线$|x|^3+|y|^3=1$才是“最完美的图形”,因为3范数的世界动点绕原点旋转的轨迹就是曲线$|x|^3+|y|^3=1$,所以3范数世界里的生物从各个方向看(转着看)这个图形都是一样的。这个解释听起来是很合理的,似乎说明我们必须适应这种看法,不要把2-范数世界放到特殊的位置,但我们会看到2-范数空间确实有些特殊性。
我们的世界里旋转可以用矩阵来表示,比如点(x,y)绕原点逆时针转$\theta$角到点(x’,y’):
$$\begin{pmatrix} x’ \\
y’
\end{pmatrix}
=
\begin{pmatrix}
cos\theta & sin\theta \\
-sin\theta & cos\theta
\end{pmatrix}
\begin{pmatrix}
x \\
y
\end{pmatrix}
=\begin{pmatrix}
x cos\theta+y sin\theta \\
-x sin\theta+y cos\theta
\end{pmatrix}
$$
那么p范数下的旋转变换会长啥样?在研究p范数几何之前,我们先来看看另一种著名的几何:闵可夫斯基空间。
闵可夫斯基空间
如果我们规定距离公式为$d^2=(x_2-x_1)^2-(y_2-y_1)^2$会怎样?首先这个世界的圆变成了双曲线,双曲线的周长是无限长的!(可用线积分计算出)这个世界的圆周率为正无穷,旋转也没有周期!诡异的事不止是这些,最诡异的是有时候长度变成了虚数!因为算距离时根号下可能为负。
这么糟糕的空间很难相信它的存在,但它就是时空!四维时空中的距离表达式为$d^2=x^2+y^2+z^2-t^2$
如果$x^2+y^2+z^2-t^2>0$这里的距离就是空间间隔,我们叫“类空的”;如果小于零我们就取绝对值再开方,得到时间间隔,我们叫“类时的”;还有一些根号下恰为0,我们叫类光的。闵可夫斯基四维时空是相对论的很好的数学模型,比如著名的洛伦兹变换可以写成像我们熟知的旋转矩阵一样:
$$\begin{pmatrix} x’ \\
t’
\end{pmatrix}
=
\begin{pmatrix}
cosh\theta & -sinh\theta \\
-sinh\theta & cosh\theta
\end{pmatrix}
\begin{pmatrix}
x \\
t
\end{pmatrix}$$
其实洛伦兹变换就是四维闵可夫斯基空间中的旋转!而且这种变换不会改变向量的性质(避免了回到过去杀死你爷爷奶奶的这种悖论),即会把类空(时、光)的向量变成类空(时、光)的向量,也说明了我们只能无限接近光速(加速即旋转,旋转没有周期性)。
广义三角函数
对双曲函数我们有$cosh^2\theta-sinh^2\theta=1$,那么我们假定p范数下也有三角函数$sin_p$和$cos_p$,满足$sin_p^p\theta+cos_p^p\theta=1$。对于双曲函数,$\theta$是“双曲角”——即单位双曲线对应的一段弧长,所以$sin_p$和$cos_p$函数的自变量也是一种弧长,我们能像三角函数一样在单位圆内定义它们。
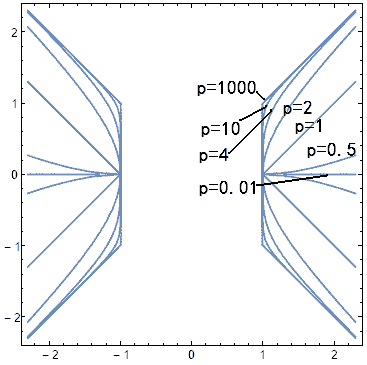
让我们来看看这些奇怪的广义三角函数的图像: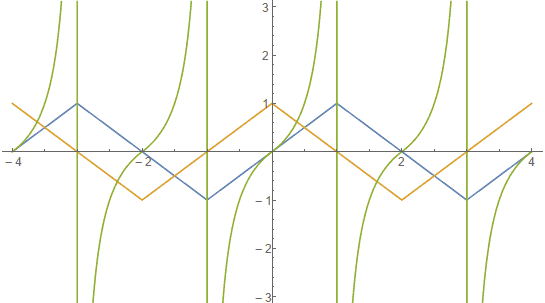
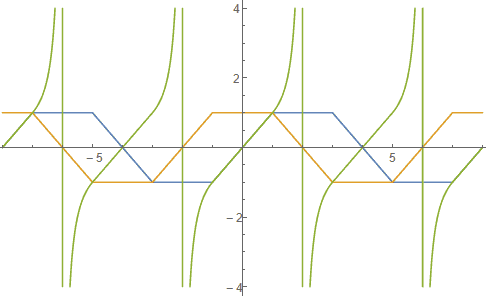
它们都是分段函数,正余弦都有种方方的感觉,正切里的曲线段则是反比例函数。
要画出像p=0.5、3、4这种不特殊的情况我们得先找到公式计算$sin_p$和$cos_p$。我们需要根据$sin_p$和$cos_p$函数的定义来算出它们满足的微分方程。三角函数的自变量是角度,函数值是对应单位圆上点的坐标,那么问题来了,怎么定义$p$范数下的角度呢?当我们遇到这种看似无解的问题时可以想想熟悉的情况,比如$p=2$时,我们是怎么在圆里定义弧度的:弧度的定义为单位圆上的弧长。但不知大家学双曲函数的时候有没有听说过双曲角这个概念,它把双曲函数的自变量解释为了双曲线中一块“扇形”的面积的两倍,所以我们也可以同样规定弧度的定义为单位圆上扇形面积的两倍,可以证明,对于单位圆中的角度与双曲线中的双曲角,这两种定义是等价的(注意用弧长定义双曲角时,计算弧长需要使用双曲距离公式$d^2=(x_2-x_1)^2-(y_2-y_1)^2$,而面积计算方法不变)。但对于$p$不等于2的场景,分别由弧长与面积定义的角度还相同吗?注意这里的弧长也要换成相应的p-范数下的距离公式计算,对于面积,我们还是暂时用同样的方式计算(算积分即可),但不排除p-范数空间中面积的计算方法已经变了的可能。
最保险是使用弧长的定义,经繁琐计算我们能得到这样的微分方程组:(注意我们的微分方程中必须加入符号函数来谨慎处理距离的定义中的绝对值符号)
$${d sin_p x\over d x}=sign(cos_p x)(1+|sin_p x/cos_p x|^{p(p-1)})^{1-p\over p} $$$${d cos_p x\over d x}=-sign(sin_p x)(1+|cos_p x/sin_p x|^{p(p-1)})^{1-p\over p} x $$$$ sin_p(0)=0、cos_p(0)=1$$根据面积的定义,我们能够算出另一个微分方程组:$${d sin_p x\over d x}=sign((1-sin_p^p x)^{1-p\over p})|(1-sin_p^p x)^{1-p\over p}|=sign(cos_p x)|cos_p^{p-1} x| $$$$ {d cos_p x\over d x}=-sign(1-cos_p^p x)|(1-cos_p^p x)^{1-p\over p}|=-sign(sin_p x)|sin_p^{p-1} x |$$$$ sin_p(0)=0、cos_p(0)=1$$
三角函数则是p=2时的特例,且以上两方程组的解相同。有了微分方程就能做数值计算了。而$sin_p$、$cos_p$的周期是p范数世界中圆的周长,所以自变量能取所有实数。
下一个问题自然就是这些函数能不能解析开拓到复平面上去呢?比如$sin(i) = i sinh 1 = 1.1752i$,这给我们一个启发:复数或许可以连接p范数世界中的三角函数和双曲函数。
下面隐藏的两个小节将讨论根据面积定义的广义三角函数的解析性质,其实跟p-范数几何关系不大,不想了解可以直接跳过。
[点击展开/收起]广义三角函数的解析性质
不同范数下的圆周率与三角函数
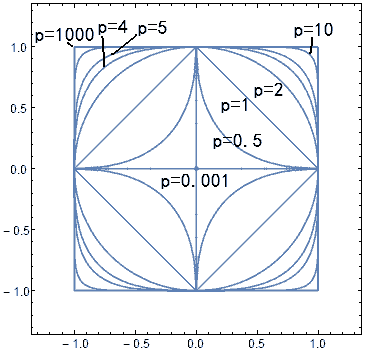
弧长与面积定义的广义三角函数到底相差多少呢?首先最明显的就是三角函数的周期不一样——这个周期对应相应圆的周长与面积。当$p=1$时,圆(菱形)的面积是2,$p=\infty$时,圆(正方形)的面积是4,但他们的周长都是8,可见这两种定义绝对是不等价的。其实从下图可以看到,它们只在$p=2$时相等。(都等于3.1415926..)其中红色曲线在p=2时还取得了极小值$\pi$!(这里有证明)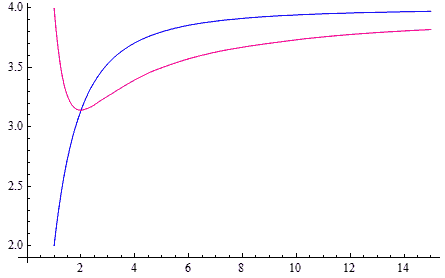
对于各种三角函数,我们不妨把横坐标缩放一下,将周期统一起来,只关注函数图像形状上的差别,看看它们的区别有多大: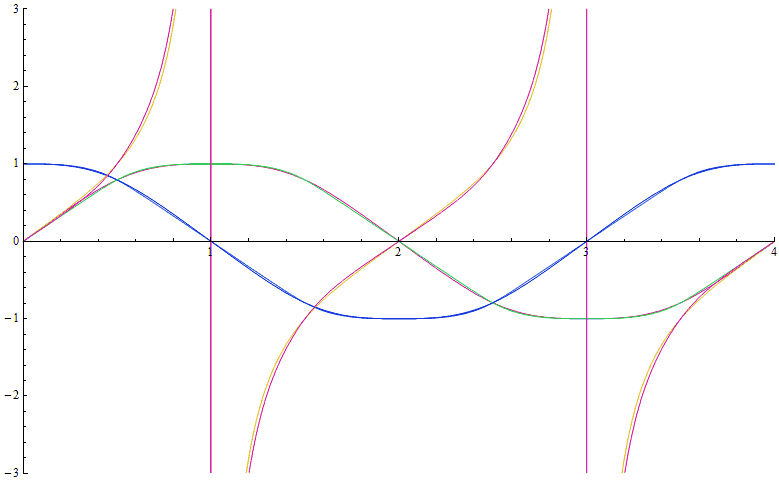
上图中画出了$p=5$时两种定义下的正弦、余弦、正切函数图像,共6条曲线,我们发现两条曲线虽然不重合,但也比较接近。
旋转对称性
回到几何上来,我们猜想p范数下也有类似的旋转矩阵:$$\begin{pmatrix}
cos_p\theta & sin_p\theta \\
-sin_p\theta & cos_p\theta
\end{pmatrix}$$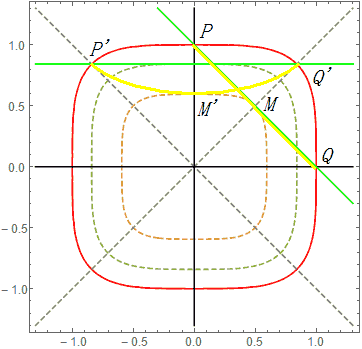
注意我们这里要严格选定弧长定义的那种广义三角函数。但不幸的是可以验证这样的矩阵变换不能保持长度不变,更进一步我们可以验证这种变换至少不是线性的,比如线段PQ旋转到P’Q’:(转了1/8个圆周)然而PQ的长度为$2^{1\over p}$,P’Q’的长度为$2^{p-1\over p}$,我们发现只有p=2时它们长度才相等。但这也不能说旋转是不可能的。事实上线段旋转完后不一定是线段,比如PQ的中点会旋转到P’Q’偏下的位置。但从等距同构群(即所有能保持图形中所有点距离不变的变换)的角度看这个世界已经不能旋转了(没有旋转对称性),等距同构群只有平移、反射变换。但这不妨碍我们定义一种广义的“旋转”——逆时针绕原点转$\alpha$角:
$$r=\sqrt[p]{|x|^p+|y|^p}$$$$
\theta=atan2_p(y,x)$$$$
x’=r cos_p(\theta+\alpha) $$$$
y’=r sin_p(\theta+\alpha) $$
其中$atan2_p$类似于$atan2$函数:表示向量$(x,y)$与x轴正向的夹角(绝对值等于夹的那段弧长)。
比如下面是p=3时的旋转: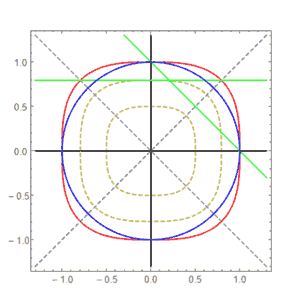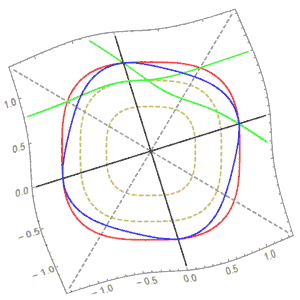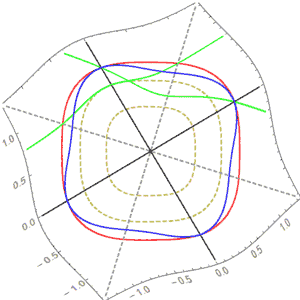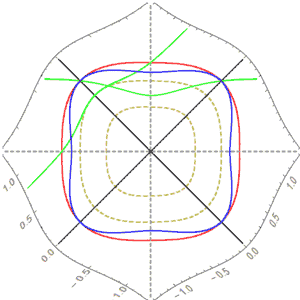
我们看到它不是线性的,且“圆”在旋转下不变,确实是最完美的图形。(我们世界的蓝色圆在这个世界中会变形,并不完美)
下面这个动画(取的p=3的世界)能反映这个旋转“不好”的性质:我们先把一个图形平移一段距离,再绕原点顺时针旋转一定角度$\alpha$,再平移回原点,逆时针转回来角$\alpha$,这个图形的形状按理说不该变,但这个旋转会让图形变形。

以下是角度$\alpha$不断变化得到的一系列变形的结果:
这种变形周期为$\pi_3/2$($\pi_3$,是p=3世界中的圆周率),且沿平移方向直线上的点没动。那是不是意味着这个世界中物体都不能转动,只能平移呢?因为试图转动会改变某些点间的距离,这个世界中的生物会认为旋转是一件不可思议的事。但我们忽略了一点:世界中的物体不一定是刚体。下面我们将建立最简单的弹簧质点模型来考察这个世界中的质点动力学,先剧透一下:最后我们会惊奇地发现,我们其实没有选择p-范数p值的权利!它将在某种意义下自动等于2。
p-范数世界中的弹簧
我们平时所说的刚体,即完全不会发生形变的物体,严格上应该定义为具有物体上各部分点在运动中距离永远保持不变的物体。怎样维持各部分点距离不变呢?最简单的做法就是硬弹簧模型:我们把刚体分成无数个质点,两两之间都连接上一个劲度系数特别大的弹簧,且弹簧的原长刚好等于质点间的距离,这样距离上一旦有变化质点就将受到回复力的作用尝试回到平衡位置上去。但这将导致弹簧振荡,我们加入适当的阻尼项让弹簧停在平衡位置。这样就近似实现了距离不变的力学约束。下面我们来看看胡克定律:
$$F = -k\Delta x$$其中$\Delta x$是弹簧的伸长量,既然涉及到长度,我们自然就要用上p-范数的距离公式来计算,这样就得到了p-范数世界中的弹簧模型。
首先我们将一个质点放在x轴(1,0)上,与坐标原点用弹簧(原长刚好为质点到原点的距离)相连,然后给它一个y轴方向上的速度,这个质点就会逆时针绕原点旋转起来。但由于我们的平衡位置已经限定好用p-范数计算,所以质点的旋转轨迹不是2-范数的圆,而是p-范数的圆。此时我们计算一下质点的速度大小,注意计算速度时也需要用p-范数的长度公式还计算速度向量的长度,但不幸的是这个速度向量的值在旋转中会改变:运动到对角线方向时质点的速度比过x、y轴时慢一些。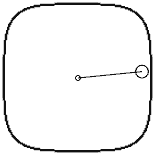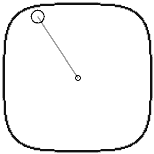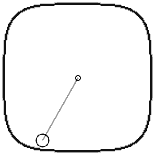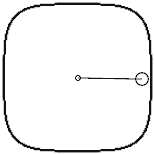
当然这也还好,我们继续增加一个质点,放在y轴(0,1)上,将它分别与原点和x轴的质点连接,组成一个三角形。同样,我们给x轴上的质点一个沿y轴的初速度,这样两个质点便会一起旋转,但我们发现这次两个质点的运动速度更加不均匀。注意这个空间里我们无法再准确定义内积、垂直等概念,所以所谓“正交分解”是进行不下去的。(其实脑洞大一点还能定义一种将p个向量映射成一个数的“内积”,这样向量范数就还是向量自身的内积在开p次方,但好像除了这个就没任何意义了)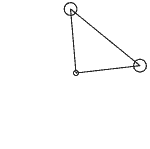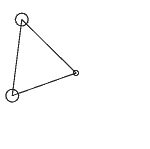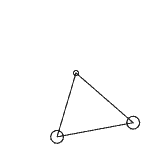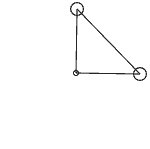
上图中的两个质点好像在相互拖拽,但那个不断变形的三角形的三边长确实是固定的!看来三边相等来判断三角形全等在一般p-范数下也不成立了。我们继续再加一个质点,这次放在x、y轴的对角线(1,1)上,加上原点四个点组成一个正方形。我们对正方形的四个顶点两两都安上弹簧,一共6个,现在我们再对一个点给一个初速度,这个正方形会转起来吗?之前我们说p不等于2的世界是不能旋转的,那会不会正方形真的只会平移呢?计算结果很奇怪: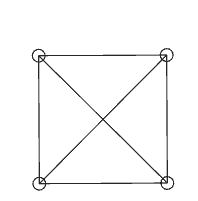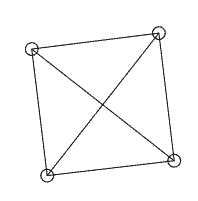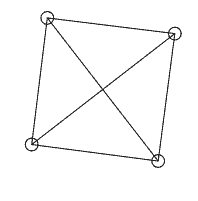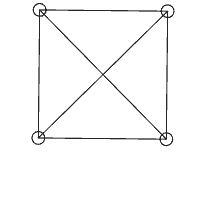
正方形还是在尝试旋转,并且最初旋转进行得很顺利,但当角度稍微大了一点后我们看到质点开始发生抖动,说明质点间的距离已经不能均保持原长,且无法自动恢复到平衡位置。更神奇的是,抖动了一会后整个正方形突然旋转了90度又稳定了下来(数值不稳定已经发生,后续又稳定没有物理意义了),但过一会就又突然转回来,直到数值计算误差过大导致整个系统剧烈抖动。但我们能够看出这个正方形并不会乖乖地平移,它还是想旋转,而且长度约束不满足后弹簧产生的内力并不能阻止旋转运动,导致整个系统剧烈震荡崩溃。
我们再来分析一个离心运动的案例:把原长为0的弹簧一头系在原点,另一头放个质点,给质点初速度会怎样。由于弹簧没有原长,所以受力的大小直接是坐标到原点的距离乘以劲度系数。我们唯一的问题是怎样将力分解到坐标上。注意给定坐标$(x,y)$后我们可以求出这个方向上的单位向量:$(x/\sqrt[p]{x^p+y^p},y/\sqrt[p]{x^p+y^p})$,读者可以自行验证这个向量是单位长度且与$(x,y)$平行。所以受力分解的结果为单位向量乘以长度$l=\sqrt[p]{x^p+y^p}$再乘劲度系数$kl$,也就是说最终力的表达式为$(kx,ky)$,表达式完全跟$p$无关!而且更加“可气”的是,只要$\vec{F}=k\vec{x}$,那么质点运动轨迹就一定是线段、椭圆或圆,注意这里的圆是2-范数下的圆,它是$\vec{F}=k\vec{x}$决定的微分方程自然的解,也就是说无论我们怎样选择范数,最终物理系统的行为都会自动满足2-范数!这也说明了2-范数的特殊性以及为什么没有更多人去深入研究p-范数几何的原因。
p-范数世界中的天体运动
上面的弹簧$\vec{F}=k\vec{x}$只是有心力运动的一个特殊情况,一般我们设$F=kx^n \vec{e}_x$,n取一为胡克定律,n取-2则为万有引力定律(Hint:三维空间中才是平方反比哦)。把单位向量写开就是$\vec{F}=k||x||^{n-1}\vec{x}$,也就是说其实只有n=1的胡克定律才与范数无关,而在p取不同值行星受引力运动轨迹也是不一样的!让我们看看p-范数中的行星系统吧!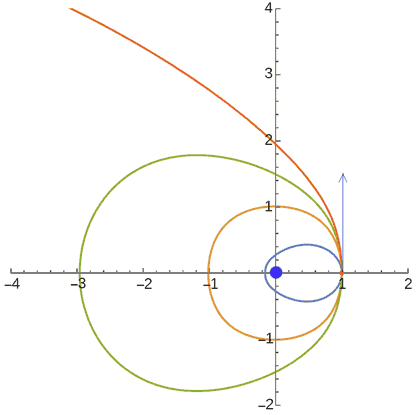
计算发现,4-范数下卫星的轨道居然是稳定的!(这里感谢热心网友的指正(2023.01.01),我最先算错了以为轨道像三次方反比那样不稳定)跟2-范数下一样,行星存在封闭轨道与开放的轨道。上图中地球放在坐标原点,放在坐标$(1,0)$处的卫星如果初速度(蓝色箭头方向)合适则能得到“正圆”轨道(橙黄色),如果初速度小一些则得到扁的类似椭圆的轨道(蓝色),速度大一些则是一个长一些的椭圆轨道(绿色),如果速度太大,达到逃逸速度则会飞出去(橙红色)。这一切都与我们的天体运动规律如此相像!但要注意的是,那个橙黄色的“正圆”轨道并不是4-范数下的圆形,它们之间的形状会有一点差异,我们稍后会进一步讨论。
平方反比的衰减律是三维空间的普遍的力(引力、电磁力等)的自然衰减方式。随着衰减幂次的变化,p范数下的轨道同样会像2-范数那样有时进动形成花瓣形轨道。然而之前在参观四维世界这篇文章中说,如果力按三次方衰减则仅存在逃逸轨道、坠毁轨道与“正圆”轨道,且“正圆”轨道还是不稳定的:稍微给点扰动就会坠毁或逃逸。计算发现当范数中的p不为2时这个结论仍然成立,可见选择不同范数基本不影响轨道的稳定性!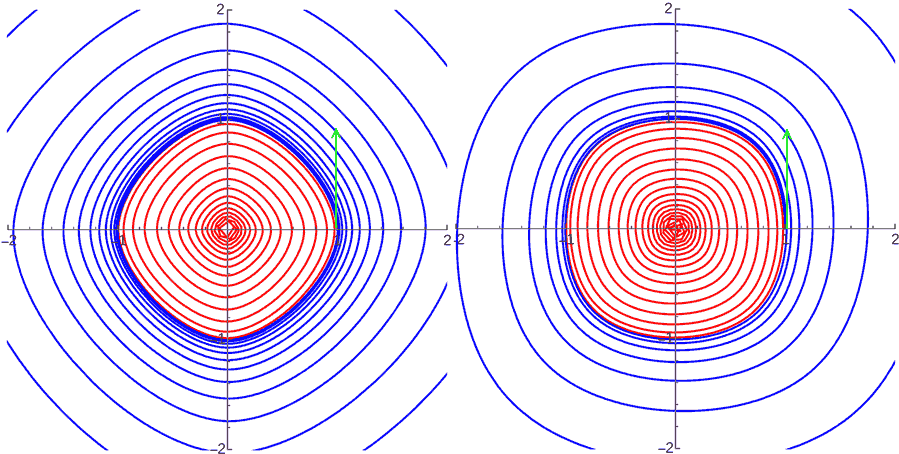
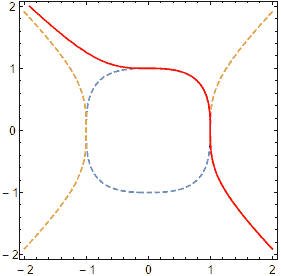
更神奇的时,这些“正圆”轨道形状在不同情形下都不一样!下面来看看平方反比、立方反比、10次方反比下10-范数空间、1-范数空间中的“正圆”轨道、这些空间中真正的“圆”三者之间到底差多少:
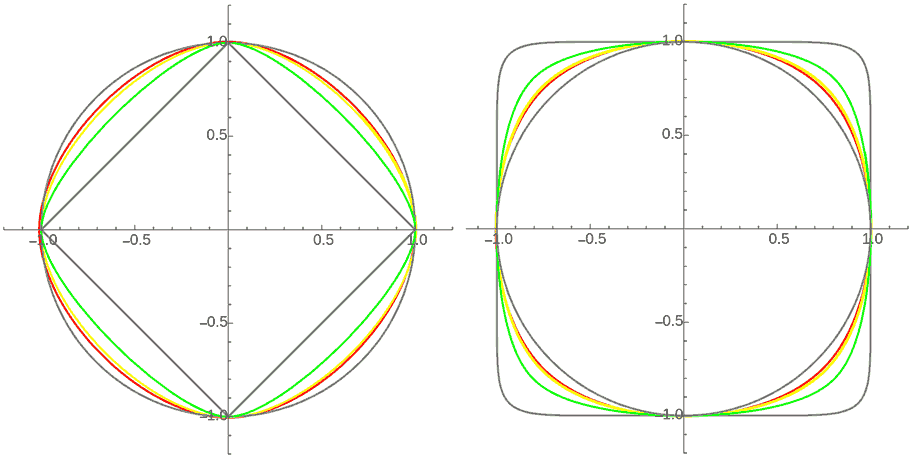
我们看到,这些稳定轨道都比p-范数的圆更“光滑”(即更接近2-范数下的圆),且引力衰减的次方数越大则越接近p-范数的圆,越小则越接近2-范数的圆(p-圆、2-圆在图中对应俩灰色图形),因为衰减的次方数小到负一就变成完全正圆的胡克定律情形了。然而这些中间的轨道有没有代数方程可以描述呢?看上去它们还是像形如$|x|^n+|y|^n=1$这样的广义圆。它们还真的是广义圆吗?会不会n次方反比n趋于无穷,它的稳定轨道就趋于p-范数的圆呢?这些问题还有待进一步探究。
其它怪异几何
我们现在总算对p-范数空间、几何有了一个初步的感知。那非欧几里得几何又是啥?非欧几里得几何其实也是2-范数空间,只是空间不平直,导致长度公式的形式跟位置有关,但永远是微元的二次形式,例如球面距离公式为$ds^2=dx^2 sin^2 y + y^2$,其中的坐标$(x,y)$分别是球面上的纬度与经度。我们把距离微元永远都是二次形式的所有空间(包括弯曲的)称为黎曼几何。其实像p-范数这种无法定义内积的空间也可以是弯曲的,叫Finsler几何,它是黎曼几何的推广,或者说黎曼几何是Finsler几何的一个特例。Finsler几何很怪异,但一般黎曼几何中的概念还是都可以推广过来。除了无法旋转物体,还可能遇到从A走到B是直线(准确说是测地线),但沿着那条路倒回来走却不再是直线的情况!下面是我看到知乎的一个问答上找到的一些对Finsler几何的描述:
Finsler几何是把切空间上的内积换成了一般的范数,每个切空间不再是一个内积空间,而仅仅是一个赋范线性空间。
如果把黎曼几何比喻做现实地球上的情况,有高山峡谷凹坑,使得最短距离不再是直线,那么Finsler 几何就相当于一个刮着猛烈飓风的地球,在这上面,顺风和逆风或者侧着风都会有很大的不一样。