群论系列(一)：群论简介

为什么五次方程没有根式解？伽罗瓦用群论做了完美的回答。群论的历史和介绍我强烈推荐这篇文章《有限单群：一段百年征程》。
但我们具体需要哪些知识才能理解伽罗瓦的理论呢？一般大多数专业的工科生都没学过群论和抽象代数，我打算写一系列文章，希望从零基础开始解释这一切。我们的主线是理解伽罗瓦的理论，当然群的用处还很多，数理化都有应用，我会写一部分其他应用。

目录

• 什么是群
• 循环群
• 子群
• 陪集与拉格朗日定理
• 对称群
• 商群
• 交错群
• 单群

什么是群？

如果你对群的概念比较清楚则可以跳过此节。简单的说，群就是一个定义了满足一定要求的乘法运算的集合体G。这些要求叫做“群公理”：
设 a, b 和 c 是 G 的任意元素。则有:

1. 封闭性。 a*b 在 G 中；
2. 结合律。(a*b)*c = a*(b*c)；
3. 单位元。存在一个 G 中的单位元 e 使得 a*e = e*a = a。 G 的单位元 e，能推出e是唯一的；
4. 逆元。对于每个 G 中 a，存在一个 G 中的逆元 x 使得 a*x = x*a = e。a 的逆元 x 能推出是唯一的。

定义里说的乘法运算并不是真正的乘法，只是满足一定要求的运算，我认为叫它“复合操作运算”更不会让人误解而想到乘法，我们只是记作*：a*b代表先做b操作再做a操作。（从右到左的写法只是为了和复合函数$f*g(x)=f(g(x))$的写法习惯保持一致）
显示用加法的例子对这四条公理的详细解释

1. 首先，一个群的集合里的每个元素都是一个“操作”，每两个元素都能相乘，得到集合中另一个元素，即两个操作的复合。比如整数和整数的加法运算就是一个群，元素n代表的操作就是 +n 运算，元素n和m的复合就是操作 +n+m = +(n+m)，对应元素 n+m。
2. (a\*b)\*c = a\*(b\*c) 是因为等式两边都表示“先c后b再a”的复合操作。
3. 群里面还有要求要有“单位元”，即“不操作”，比如加0运算，这种操作与任意操作a复合还是操作a。
4. 群里面的乘法运算这样定义太宽泛了，似乎所有操作都能满足，于是我们规定每个操作都在群里能找到对应的“逆操作”，使得这两个操作的复合是单位元“不操作”。比如加法运算 中 +n 的逆运算是 -n，复合的结果是加0。所以整数和整数的加法运算满足群的要求，但自然数中的加法就不行，因为加自然数的逆运算是负数，不在自然数集合中了。

注意：群公理中不要求乘法有交换律，这意味着两个交换顺序的操作是不一样的，比如矩阵乘法和几何里面的旋转与平移：设想一个人先前进一米再左转90°，与先左转90°再前进一米，最后结果是不一样的。

一些例子

群的用途不是让我们检验哪个数集上的四则运算是否符合公理，而是研究某些有共形的操作的集合的性质，比如在一个对称的图形中，我们把所有能保持图形不变的变换放入一个集合，这些变换反映了图形的对称性，它们构成了一个群，叫图形的对称群，比如有8种能让正方形不变的操作构成了群$D_8$。显示具体8个操作

1. 不操作
2. 向右旋转90°
3. 向右旋转180°
4. 向右旋转270°
5. 垂直翻转
6. 水平翻转
7. 对角翻转
8. 另一个对角翻转

我们知道了这些又有什么用呢？其实我们关心的并不是这些操作本身，而是这些操作复合运算的整体结构。比如群$A=\lbrace ×1操作，×-1操作\rbrace$与群$B=\lbrace不操作图形，水平翻转图形\rbrace$描述的是完全不同的操作，但它们的结构一样：都是有着一个单位元，另一个操作是自己复合等于单位元。我们认为这两个群在同构的意义下是一样的。同构是指两个群中的元素存在一一对应的关系，且乘法的结果也能一一对应。这使得我们能够抽象地研究群论。上面描述的群叫二阶循环群（Cyclic group），记作$C_2$。我们说一个群的阶就是群元素的个数。下面我们就来看一些抽象的群的例子：

循环群

先形象解释n阶循环群：由操作“旋转1/n圈”生成的群。这里的“生成”指的是包含给定操作的最小的群。由于群里乘法封闭性，我们能推出操作“旋转k/n圈”（k从0取到n-1）都该在群里，我们能验证这些操作的集合已经满足所有群公理，于是这就是操作“旋转1/n圈”生成的群了。我们给操作“旋转k/n圈”编号为k。
n阶循环群的严格定义是群$G$里存在一个元素$g$，$G$中每个元素都是$g^k$($k\in Z$)的形式。这里元素的幂代表自己与自己复合k次。
在“同构”的意义下，循环群还能看成是“模n的同余类构成的加法群”，看起来很复杂的样子，其实就是集合{0,1,…,n-1}上定义的加法运算：如果两数之和大于了n-1就去除以n的余数以保证结果落在集合内（封闭性）。注意这个群中的乘法满足交换律（因为定义的加法运算自然又交换律），是个交换群（也叫阿贝尔群）。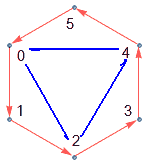

子群

观察一下我们注意，在$C_6$群里面取三个元素{0,2,4}，它们也能满足群公理，也就是说这是$C_6$群的子群，类似于子集。群{0,2,4}同构于$C_3$（蓝色的三角形），其实{0,3}也是一个子群，同构于$C_2$。注意只包含单位元的集合{0}和全集{0,1,2,3,4,5}也是子群，但这两种情况没啥意义，我们说它们是平凡子群。像不像任意数都可以被1和它本身整除？这样我们可以定义类似于质数类似的概念……我们先就此打住，回到子群的讨论中，确实有类似质数的概念——单群，但它的定义不是这样的，等讲完正规子群我们再回头讨论。
还有其它子群吗？我们可以慢慢找，但拉格朗日定理告诉我们子群的阶一定是原来群的阶的约数（群的阶 = 群元素的个数），就是说$C_6$群的子群中只有1阶（{0}）、2阶、3阶、6阶（自身）群。这样大大缩小了我们找的范围，我们发现2阶、3阶子群都只有一个，分别是{0,3}和{0,2,4}。于是，$C_6$一共4个子群。

陪集与拉格朗日定理

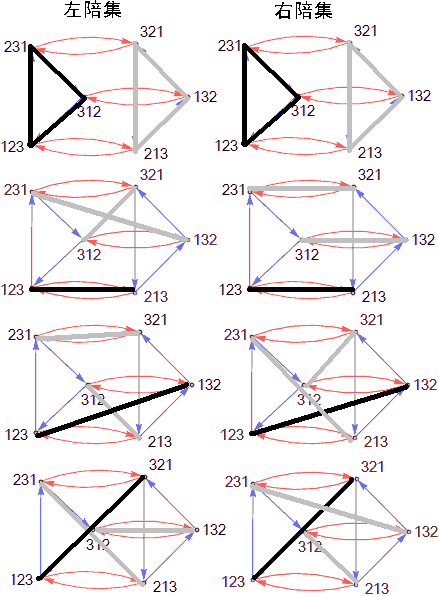
子群比子集的要求强多了，因为子群内部要求乘法封闭性。设群G有子群H，任给一个群G的元素g都可以与子群H中所有元素相乘（若不是交换群，则统一左乘或统一右乘）,得到的结果组成一个新的集合，叫陪集，记作gH或Hg（统一左乘得到左陪集，统一右乘得到右陪集）。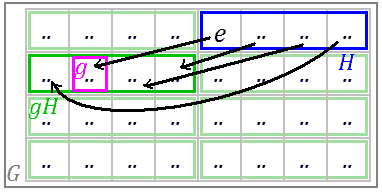

不同的陪集之间是不相交的，以左陪集为例，我们分两种情况：

• 如果g本来就是子群H中的元素，由于封闭性，得到的结果也在子群H中，而且所有结果刚好就组成了集合H。如果不刚好是集合H，说明g乘以H中某两个元素得到了同样的结果，这与群里逆元的唯一性矛盾。
• 如果g不是子群H中的元素，得到的结果构成的集合元素个数一定等于子群H的阶数（还是因为逆元的唯一性），且两个不同的元素对应的陪集g1H、g2H要么相等，要么交集为空。
  显示证明 设左陪集（右陪集同理）$g_1H$、$g_2H$相交，即存在$h_1、h_2\in H$使$g_1h_1=g_2h_2=c$，则$g_1=g_2h_2h_1^{-1}$，即对任意$h$，有$g_1h=g_2h_2h_1^{-1}h$，所以$g_1H\subseteq g_2H$，同理$g_2H\subseteq g_1H$得两集合相等。

这说明这些陪集是两两不相交的,且所有G中元素都在某个陪集中——G可以被分解为左（或右）陪集的并，而陪集元素个数就等于子群H的阶数，所以H的阶整除G的阶。整除得到的商，即左陪集个数和右陪集个数是相等的，叫做H对G的指数。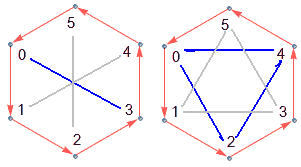

上图左边二阶子群有三个陪集（记住子群自己也是陪集），右边三阶群有两个陪集，整个群的阶为6。

对称群$S_3$

在我们讲下一个抽象的概念之前我们先来看看其他的一些群。注意这里的对称群不同于几何图形的对称群：对称群$S_n$指集合{1,2,..,n}上所有到自身的双射的集合，通俗地说就是{1,2,..,n}的全排列所代表的置换操作，我们来看例子$S_3$：
{1,2,3}的全排列有3! = 6个，分别是：123、132、213、231、312、321。
其中123是“不操作”，132是“交换第二、第三个数”，我们简写为“2->3,3->2”，213是“2->1 1->2”等等。
我们取两种特殊的操作a=213（交换1和2），b=231（轮换），可以画一种图来表示这6个元素操作间的复合关系：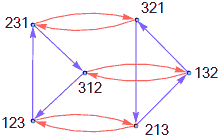

蓝色箭头表示操作b=231，红色表示a=213。我们发现其他元素都可以用这两个元素和它们的逆的乘积表示，说明了a和b是$S_3$的生成元。这种用把生成元画成箭头的方式来表示群的方法叫凯莱图(Cayley Graph)，前面看到的循环群画的图也是凯莱图。
你能找出多少个非平凡子群来呢？能画出它们的陪集吗？
显示答案



注意这个群不是交换群，因为这些置换操作改变顺序会得到不同的结果，事实上$S_3$是最小的非交换群。当在找它的子群时通过拉格朗日定理我们知道非平凡子群的阶一定是2和3，由于子群一定得包含单位元，所以是不是我们还需要尝试5 + 5*4 种可能情况呢？有没有快速找子群的技巧呢？首先我们标出每个群元素的阶——这是与群的阶不相干的两个概念——元素g的阶就是使$g^k=e$的最小的正整数k。如果除了k=0，找不到$g^k=e$，就规定元素g的阶是无穷大。当然在有限群中所有元素的阶都是有限值，不然由于乘法封闭性，$\lbrace g^0, g^1 , g^2.. g^\infty \rbrace $都会在集合中。$S_3$中有2个三阶元素231、312，3个二阶元素213、132、321,一个一阶元素123。这里要用到一个拉格朗日定理的推论：所有元素的阶都整除群的阶。因为有n阶元素存在说明它一定在群内生成了一个n阶循环子群，子群的阶n必整除群的阶。我们发现每个二阶元素都能生成一个循环群$C_2$（一共3个），2个三阶元素生成了同样的子群$C_3$，如果子群同时有二阶、三阶元，则子群的阶为6，这是平凡群。所以$S_3$的所有非平凡子群只有4个。
注意对称群$S_2$和循环群$C_2$等价，所以一个群可以用很多不同的理解方式。（同构的意义下）

更复杂的对称群

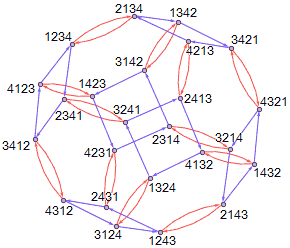
我们看到了$S_3$的凯莱图是个三棱柱，下面$S_4$的凯莱图居然是个半正多面体的球极投影！这个半正多面体叫小斜方截半立方体，由正方体切棱切顶点后得到，八个蓝色三角形对应正方体被切掉的8个顶点，6个红色的正方形对应原来正方体6个面被切后剩下的部分……（喜欢正多胞形的我忍不住多说几句）

当然生成元的选择不是唯一的，所以我们能得到不同样子的凯莱图，它们都表示同一个群，难以想象吧。

这是一个？截角八面体。
再下一个对称群——$S_5$的阶为$5!=120$。这个群太庞大，凯莱图就不好看了，Mathematica画出来一团乱麻，这个群在论证五次方程为什么无根式解中有重要地位，这里先就不说了。

商群

我们再来关注一下陪集。每个陪集中的元素个数和子群元素个数是一样多的，这导致感觉上陪集就是子群的一个个副本。有一种说法是陪集是群G中元素对子群H的操作，这种操作也叫“平移”，元素g作用于子群H，便把集合H“平移”到了gH。我们能不能把陪集看成一个整体，给两个陪集间定义乘法运算，使所有陪集构成一个群呢？答案是只要一个子群H的所有左右陪集相等，我们的愿望就能实现。这个新的群叫商群，记作$G/H$。简单形象地解释一下陪集间的乘法：从两个陪集中各找个“代表”元素来相乘，它会落在新的陪集里面，这个新陪集就定义为两个陪集相乘的结果。

我们为什么要搞出“商群”的概念？维基百科给的理由是来自整数的除法。在12除以3的时候得到答案4是因为我们可以把12个对象重新分组为含有3个对象的4个子集。商群出于同样想法，但用一个群作为最终答案而非一个数，因为群要比对象的随机集合要更有结构。

不是任何子群都是整个群的“因子”（像整数约数那样），只有左右陪集相等的子群才是，我们叫正规子群，记作$H\lhd G$。
显示商群的具体定义

如果集合$N$是$G$的正规子群，则：
我们定义集合$G/N$是$N$在$G$中的所有左陪集的集合，就是说$G/N = \lbrace aN : a\in G \rbrace$。对于每个$G/N$中$aN$和$bN$，$aN$和$bN$的乘积是 $(aN)(bN)$。这个运算是闭合的，因为 $(aN)(bN)$实际上是左陪集：
$(aN)(bN) = a(Nb)N = a(bN)N =(ab)NN =(ab)N$。
注意：N的左右陪集相等被用在了这个等式中。

商群的例子

整数集上的加法构成群$Z$，所有偶数的加法也能构成群，记作$2Z$，它是$Z$的子群。我们不难发现这个子群有两个陪集：{所有奇数,所有偶数}，由于偶+偶=偶，偶+奇=奇+偶=奇，奇+奇=偶，这说明陪集间的运算构成了群，且它同构于循环群$C_2$（或对称群$S_2$），即循环群$C_2=Z/2Z$。[显示]为什么同构？

说它同构于循环群，理由：偶对应不操作（或+0操作），奇对应转半周（或+1后再取除以二的余数）；说它同构于对称群，理由：偶对应不操作(12)，奇对应交换(21)。
其实这种情况能推广到所有循环群，有$C_n=Z/nZ$。
我们再看看有限群上的例子：由于循环群是交换群，所以所有子群都是正规的（左右陪集相等），我们有 $C_{mn}/C_m=C_n$。

交错群

交错群是对称群$S_n$中的子群，记作$A_n$，它是由$S_n$中所有偶置换构成的群。置换的奇偶性指的是把置换分解为多个对换（即每次只交换两个数的位置）的叠加，可以证明给定一个置换，不论什么分解方式，最后得到的对换个数的奇偶性不变。这样所有的偶置换组成了一个子群，所有的奇置换组成了这个子群的陪集，我们可以证明它是正规的，且有$S_n/A_n=C_2$。

小时候有种拼图游戏（大多数是图案，而不是数字，但本质一样）的所有操作就是把这些方块换到正确的位置，但如果我们想通过操作只交换某两方块位置（比如交换14和15）是不可能的，因为每操作一次空位就会改变位置，每次操作实质是空位与相邻某方块对换。而只有偶数次移动才可能使空位回到原来的位置，即我们只能实现偶置换，而单纯交换某两方块位置则是奇置换，是不可能做到的。

单群

现在我们能够定义类似质数的概念了——单群——如果一个群的正规子群都是平凡的（{e}和它自身），这个群就叫单群（也叫简单群）。比如所有的质数阶循环群都是单群。有限群中哪些群是单群这个问题很有意思，详见文章《有限单群：一段百年征程》。

正是交错群$A_5$是单群而直接导致五次方程没根式解。(未完待续)