

在前面讲解《维度数学漫步》的系列文章中,我曾经提到过影片中出现的一个圆盘图案,它是《维度数学漫步》第二集《三维空间》中的那个房间里的装饰。这一集的讲述者是埃舍尔(Escher),那个圆盘图案和那些蜥蜴都是他的作品。影片着重讲述的是那些二维蜥蜴的一只从他的画里面逃出来,它该如何向它的二维同伴们解释三维空间存在的故事。而那个作为装饰的圆盘图案只是一晃而过,其实这个图案和四维空间一样精彩:它就是双曲空间中的双曲镶嵌。
网上能搜到很多关于埃舍尔的这些画,但里面具体的数学内容却几乎没有提及到。下面我们就主要说说双曲镶嵌的数学含义,然后我们自己怎么来画一幅这样的画——用电脑画——在线演示在这里!(附双曲镶嵌版熊猫表情!),当然你足够NB也可以像埃舍尔那样手绘!
双曲几何、欧氏几何与球面几何
这三个概念应该是最普及,网上介绍得最多的了。它们来源于欧几里得的《几何原本》提出的第五条公设,即过直线外一点有且只有一条直线与已知直线平行。第五条公设如果成立就是经典的欧氏几何(比如初高中的平面几何、立体几何),第五条公设不成立的最好理解的例子就是球面几何。球面上的直线就是过球心的大圆(因为球面上连接两点的最短线路是大圆的一段劣弧),任意两个不重合的大圆都会至少交于两点,即不存在两条直线平行。双曲空间相反,说的是过直线外一点有无数条直线与已知直线平行,这里平行即指不相交。为什么要叫“双曲”空间呢?因为它是双曲面上的几何。但这个双曲面上度量长度的方式是很怪的,是闵可夫斯基空间的度量(对!就是四维时空的度量方式!)。这种度量下的双曲面就是到顶点距离为定长的点的集合!闵可夫斯基空间中的生物(如果有的话)会认为双曲面是最完美的几何体!所以我们不会太习惯这个模型。
庞加莱共形圆盘模型

就像球面几何一样我们可以用球极投影(还记得球极投影吗?《维度》第一集就讲的它)来展示这个球面,双曲几何也能把双曲面投影到平面上来展示,但与球极投影不同的是双曲几何平面上的投影只在一个圆中。埃舍尔的那个圆盘正是庞加莱共形圆盘模型。
你可呢会说这个模型这么丑,居然周围的图案都拉长了,没有保角性。但其实它是有保角性的!只不过这里的角是闵可夫斯基空间中的双曲角!双曲角你可能不知道是啥,但双曲函数我想应该不陌生吧。
当我们用广角镜头调整角度看整个双曲面。直到一个特殊的角度时,整个双曲面看上去就是一个圆了。即从一点投影(类似球极投影的北极点):

注意与球极投影一样,投影是保角(共形)的,但这个投影“吞并”了反映闵可夫斯基空间的特殊方向,所以得到的圆盘中的角不再是双曲角,所以我们才能能明显看到角度相等。但投影会改变图形的大小,也就是说其实这些图形的大小都是一样的,只不过投影让我们看到越接近圆盘的边缘物体看起来的大小越小。(想想生活中的透视投影:近大远小)所以这个单位圆盘其实是一个无限大的世界!这不难理解,因为它是双曲面的投影,而后者就是无限大的;而球面几何则是一个有限的封闭空间上的几何。它们的本质都是一种弯曲的空间。
以后我们就研究这个圆盘中的几何学。这个空间中的直线是与圆盘正交的圆弧,可以看出过一点能作无穷条直线与之平行。
双曲房间
一个单独的一无所有的空间是没意思的,不能可视化这个空间。所以我们可以用镶嵌(密铺)的方法,用多边形密铺整个双曲空间。平铺的结果就是你看到的埃舍尔的画。当然这个世界的多边形的边都是双曲空间中的直线段,即圆弧。
《维度》制作人之一josleys网站上的一篇文章《Hyperbolic Chamber》给了一种可视化双曲空间的生物在他们的世界里看到的情景:把多边形的边换成镜子(镜子当然是圆弧的),然后人站在里面就可以近似地体验弯曲的双曲空间了。

当然,有二维的双曲空间就自然有三维的、四维的……三维的双曲镶嵌可视化也能用这种房间。更多图片请访问josleys的文章。
双曲空间和球面空间都是有常曲率的,所以没有缩放不变性,因此除了全等,你找不到两个相似的三角形。
看到这里我们大概会有种疑惑,那就是到底有几种正多边形双曲镶嵌?如果我们要构造一个镶嵌满足:n边形、每个顶点发出p条边,则必须要有:
$$\frac{1}{n}+\frac{1}{p}<\frac{1}{2}$$
如果等于1/2就是传统平面上的欧几里得镶嵌了,如果大于1/2则是球面镶嵌。球面镶嵌又是啥?球面正多边形镶嵌只有五种,对应五个正多面体!正多面体的本质就是正多边形球面镶嵌!所以正多胞体的本质是超球表面的正多面体镶嵌!有正多面体就有半正多面体(多种正多边形为面的凸多面体),所以双曲空间还有多种正多边形的复合镶嵌……
根据前面的式子可得出答案正多边形双曲镶嵌有无穷多种,最牛的是双曲空间中允许正无穷边形的存在!(注意这里的正无穷边形不是圆)如果你愿意你还能让每个顶点发出无穷条棱!
这里我们可以看到球面几何空间是一个有限封闭的空间,而欧几里得平面几何和双曲几何空间都是无限大的空间,而且在某种意义上双曲几何空间比平面几何空间更大。
莫比乌斯变换
还记得《复数(上)》讲分形前用照片做共形变换吗?其中复反演变换z->1/z是最精彩最好玩的变换之一。你有没有想过把自己(或你想恶搞的人)的照片放在复平面上变变形呢?我们把复数域中的一次分式变换$(az+b)/(cz+d)$叫莫比乌斯变换。(莫比乌斯变换跟莫比乌斯带又是啥关系???)
- 我们的欧几里得二维空间中的平移、旋转缩放都是莫比乌斯变换。
- 如果我们认为球极投影投到了复平面上的话,那么滚动球体复平面上投影的变换就是一种特殊的莫比乌斯变换。特别的把南北极颠倒正对应变换z->1/z!
- 如果我们认为庞加莱圆盘模型对应复平面上的单位圆,则在双曲空间中的平移、旋转、反演等变换都是莫比乌斯变换。
那你可能会问,三维的双曲空间、球面(其实是四维超球面)空间上的变换由该用什么表示?答案是四元数的莫比乌斯变换!四元数是复数的四维推广。(因为三元数无法推广,所以三维空间也要用四元数表示,多余的维度可以一直置0)
有了莫比乌斯变换我们就能用计算机方便画出这些双曲正多边形镶嵌了。方法是先计算出中央双曲正多边形,然后通过不断莫比乌斯反射变换,像双曲房间照镜子那样复制多边形来填满整个圆盘。具体细节这里就不详细说明了。josleys的《Hyperbolic Chamber》上讲了具体的做法。
奇形怪状的世界
既然复数的共形变换变照片很有趣,为什么不变变有镶嵌的庞加莱圆盘呢?其实根据黎曼映射定理任何单连通(没有洞)的图形都能共形地映射到单位圆内,反之亦然。
- 通过莫比乌斯变换可以把单位圆内部变换到半平面(可以想成过极点的圆变成了直线),得到半平面模型。
- 反双曲正切函数变换可以将单位圆盘变成一个无限长的带子,叫带状世界:$$B(z)=\frac{4}{\pi}\mathrm{arctanh}(z)=\frac{2}{\pi}\ln\left(\frac{1+z}{1-z}\right).$$

- 最后是在带状世界的基础上再做一个指数变换,我们就能得到圆环,叫环形世界。有部科幻小说就叫《环形世界》。$$A(z)=\mathrm{e}^{\Large\frac{i2\pi(z+i)}{kP}}$$
其中参数P是带状世界水平方向的周期,所以给定了一个镶嵌带状世界的的周期是一个固定值,如果选其他值会导致环出现一个断层接不起来,这也导致环形世界的等距变换少了一个自由度。参数整数k可自行调节,是环一圈出现带状世界的周期数,k越大,周期越多,环越细。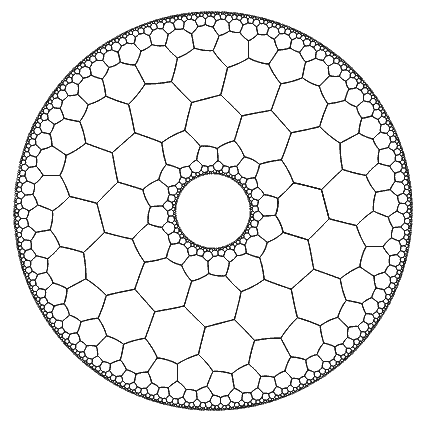
受josleys另一篇文章(法语,建议可翻译成英语读)启发,我们改一改指数映射的表达式就能得到漩涡世界: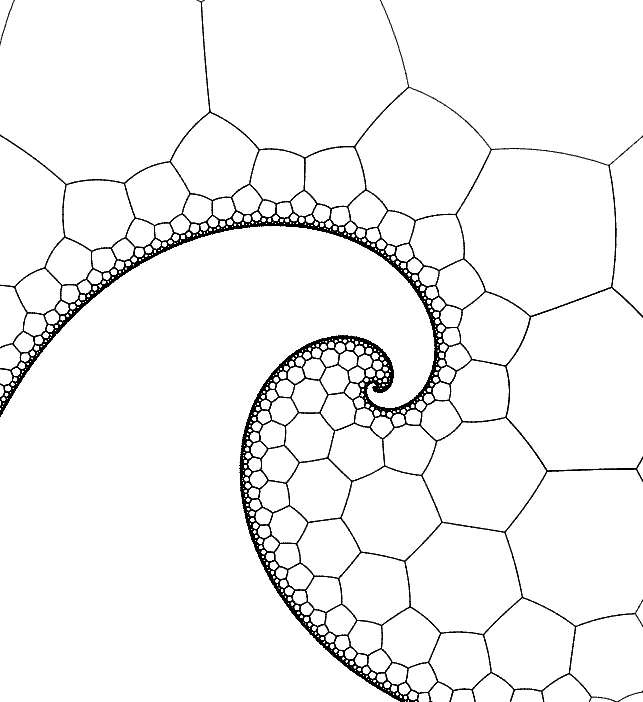
- 这个网站上有很多精彩的图形(其中我最喜欢的是把庞加莱圆盘映射到Julia集的外部的那个动画,觉得能盯着看100遍)里面还给了一些精彩的变换,我试着做出了这个:让我想起了化学实验用的三颈瓶,就叫它“多颈瓶”吧。(请自动忽略freemèrzé的含义)

在线演示
(我用javascript写的,电脑上Chrome浏览器最佳,点这里可单独打开在线演示页面)注意图片模式下有些图形无法计算或正常显示,因为直接画线和画图我用的算法不同,一个是正函数,一个是反函数,有些反函数是多值函数或写不出表达式。图片模式下可以加载您电脑上的图片,进入拖动贴图模式后可以设置图片在中央多边形中的位置(右键拖动可旋转放大)
最后推荐一些在网上找到的一些关于双曲空间的小程序
- 一个可视化三维双曲空间的小软件:弯曲空间
- 能在双曲空间中的数独、走迷宫、打台球:HyperbolicGames
- HyperRogue: 强烈推荐!(官网上可免费下载),前两个跟这个比起来就是小打小闹:双曲空间中的Rogue类游戏,无限地图,拥有各种奇怪的生物群系(66种!),还能充分体会到双曲几何中的直线、等距线、极限圆、圆的不同曲率,训练你在双曲空间中的寻路能力,比如找到半径为20格的圆的圆心位置比你想象的要困难、你有时发现双曲空间更像一种分形——永远无法到达中心的漩涡海(基于极限圆)、没有尽头不断分支的树等。它将双曲空间的几何性在游戏中发挥得淋漓尽致,可以说在所有二维双曲游戏中绝对排第一。(其实它也支持3D双曲空间,并且还包含三维球面、直积空间等其它扭曲的怪空间,作者的数学功底非常高)

值得一提的是它的实现原理。如果我们用庞加莱模型存储地图的话,那么离我们很远的地方就会集中在圆盘边缘,很小的地方,导致浮点数精度跟不上,所以HyperRogue的作者在程序内部用的是三维的双曲面坐标,只是最后显示时才做庞加莱圆盘投影。这里有豆瓣的中文介绍 - (22年更新) Hyperbolica 一个第一人称3D双曲世界游戏。渲染与模型上都很巧妙,但论游戏逻辑上我单方面认为远不及HyperRogue。
- (24年更新) 我自己做的游戏Deductrium(推理元素) 一个在浏览器中用Typescript实现的数学形式系统与双曲空间结合的游戏。目前包含命题逻辑、一阶逻辑、皮亚诺公理、ZFC集合论与一些序数和类型论的内容。其中序数部分充分利用了双曲空间的一些有趣的几何性质。