《维度数学漫步》第一集就讲的是用球极投影来绘制地图。但其实你我都知道,我们熟知的世界地图并不是用这种方法得到的,球极投影只用来绘制极地周围,世界地图用的另一种投影,它得到的地图也不是无限大的,而是矩形,这种投影就叫做墨卡托投影,它和球极投影一样,都是保角的。
墨卡托投影的大概做法就是先拿一个圆柱体使它的轴与地球自转轴重合,我们先把球面上的点投影到圆柱的侧面上,再把圆柱展开就得到长方形的地图了。但具体做法并不是保持z轴不变对应到圆柱上,也不是在球心放一盏灯直接投影到柱面上,为了保持保角性我们能计算出一个特殊的函数,叫古德曼函数,但北极点会投到无穷远,这样的地图是宽度有限、长度无限的,(柱面无限长)我们看到的世界地图把极地附近区域截掉了才得到有限的矩形地图。
为什么我们取的圆柱的轴要恰好与地球自转轴重合呢?我们不妨选任意的角度,那将得到你从来没有见过的世界地图!于是我在网上找了一张比较高清的矩形世界地图,通过墨卡托投影逆变换得到三维坐标,再将球面旋转,再用墨卡托投影得到我们从没见过的世界地图。我找到的地图不是严格的墨卡托投影(能在极地附近看出不保角),我只能做些尝试。最先我以为把球面上的点投影到圆柱的侧面上是保持z坐标不变的,但这种方法我得到的图像南北极都有很大的扭曲,还有一个想法就是投影后的z坐标与维度成线性关系,即对原z坐标做个正弦变换,这样得到的图像才比较正常。在我调试期间还得到了意外的收获:(已经不知道怎么得到的了)
它让我想起了刘慈欣的一部科幻小说《地球大炮》,讲的是修隧道打穿地球建立高速通道的故事。
回到正题,下面是维基百科上的选平行于赤道面的轴的圆柱:
点这里查看任意的角度墨卡托投影地图查看器
让我们做一些更有趣的事:墨卡托投影展示多面体!现在我将一个正十二面体放到球面上去,我们熟知《维度》第二集里展示的球极投影,那试试墨卡托投影呢?投影结果是这样的:
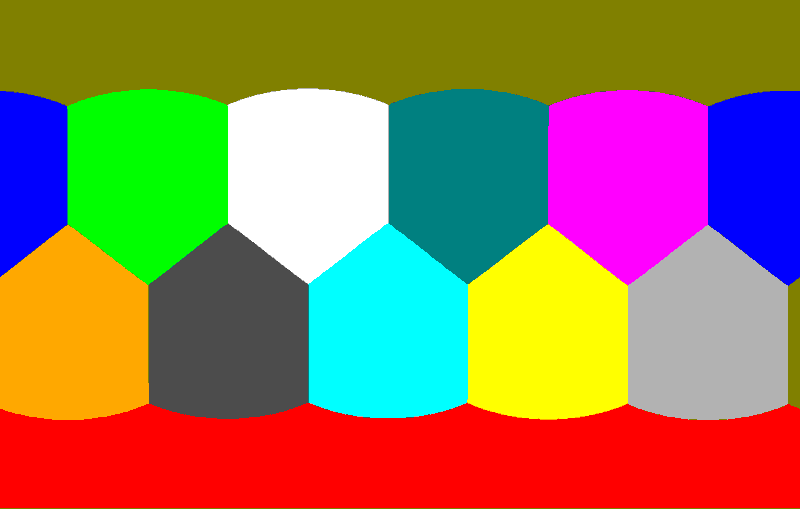

点这里查看过任意极点的正多面体墨卡托投影和球极投影的在线演示
这个演示我使用的是逆算法:遍历屏幕每一个像素,通过墨卡托投影逆变换得到三维坐标,然后判断属于哪个面以给像素上不同的颜色。具体判断方法是这个点离多面体哪个面心近就认为属于它,所以我想画多面体A就得需要A的对偶多面体的顶点数据(即多面体A面心数据),这种做法好在我不在关心顶点的顺序、边的连接方式等繁琐问题了,简单粗暴。
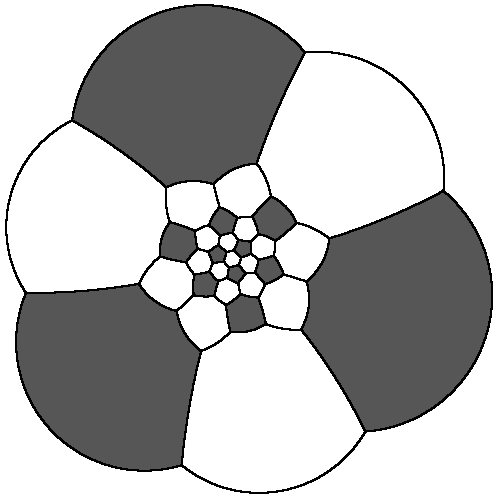
附送我做的足球的墨卡托投影和球极投影 (^-^) :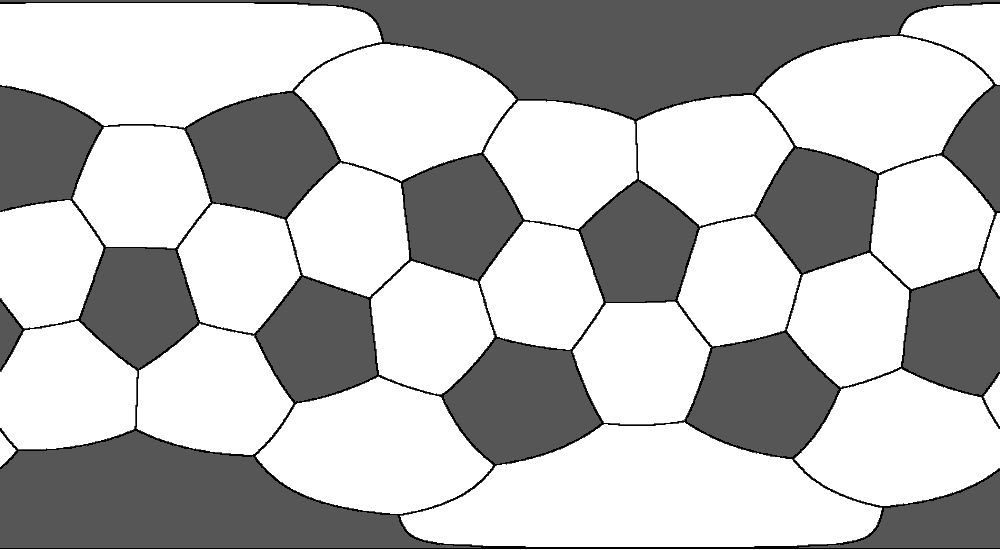
Pour aller plus loin: La Dimension 4
墨卡托投影能够类比到四维空间吗?首先我们需要球道圆柱的投影,四维有超球到球柱的投影,但球柱的侧面(球面与线段的直积)是无法展开的,我们可以再用一次墨卡托投影把球柱的侧面展开,变成长方体。但这种二次投影总感觉怪怪的。还有一种做法是直接投影到圆柱柱上,再展开成长方体,但圆柱柱是方形与圆的直积,总感觉不太好,如果我们能投影到双圆柱(圆与圆的直积)上展开更好,但双圆柱的侧面是什么?双圆柱有两个全等的曲胞围成,这种曲胞是实心圆和圆圈的直积,能够展成圆柱(把圆圈掰直),这样我们需要两个分立的圆柱来展示世界地图,也感觉怪怪的……我还没想到十全十美解决此问题的方案,欢迎大家讨论。