注:这篇文章不需要读者有专业的拓扑学基础，可能一听到“代数”就给人一种抽象难以理解的感觉，因此本文更多希望从直觉上让大家感受一下代数拓扑中的同伦、同调是什么，具体正式定义和技术细节可以在任意一本代数拓扑的书上找到哦。
四维空间（十二）：解开球面结
# 本文是《四维空间（十）：扭结与环扣》的续集，本内容对空间想象力要求较高，可能有些地方难以理解，但全文没有任何公式，只涉及几何，不涉及代数，适合挑战空间想象力哦。
# 我发现不仅是我，网上“扭结”与“纽结”全都在混用，那我也懒得改了。
在本系列的上上篇文章中我们知道了四维空间中的二维曲面打结现象与各式各样的孔、环扣等，上次对二维曲面结的介绍其实也不算太详细，只给出了一些非平凡的管状结作为例子，今天我们要从另一个角度来分析扭结。本文的主要内容来自于这个Youtube视频与这篇论文，它介绍了通过旋转三叶结的方式来构造同胚于球面的结（即允许自相交的话能把这个结恢复成球面），并且证明了有些是真正无法解开的结，另一些是能够通过一些步骤解开成球面，下面我们也来试试解一解高维空间当中的结！
本文目录：
- 纽结旋转体
- 三维扭结投影上的交点
- 新的四维图形可视化方法
- 地图上的交线
- 自转的三叶结
- 七种Roseman合法移动
- 利用Roseman移动解开它！
四维空间（十一）：几何代数、四元数与空间旋转
#警告：本文内容超级进阶，可以说大概包括四维欧几里得空间的所有基础的代数理论了，本文重代数轻几何，所以可能不太好理解
这篇文章将会介绍一种新的可以“统一天下”高维几何的代数系统：几何代数（Geometric Algebra），因为在这个代数体系下包含了标量、向量、多维向量以及各种内积外积混合积，甚至囊括到了旋量（就是让电子转两圈才一样的罪魁祸首）、空间旋转、复数与四元数，矢量场中的各种导数算子，甚至几何代数还能给行列式一个新的定义……
引子
我们在探讨四维空间中的磁场时提到过两个2-向量之间的三种乘法运算：
| 运算 | $e_{ij}*e_{ij}$ | $e_{ij}*e_{jk}$ | $e_{ij}*e_{kl}$ |
|---|---|---|---|
| 内积$\cdot$ | 1 | 0 | 0 |
| 混合积$\times$ | 0 | $e_{ik}$ | 0 |
| 外积$\wedge$ | 0 | 0 | $e_{ijkl}$ |
当时说感觉上是相同字母可以合并相消，不同字母则直接写在一起构成一个多维向量，这样组合下来每一种n-向量刚好对应一种乘法运算。我们不妨规定一种新乘法运算来同时满足上述条件。为了和内积外积区别，新的乘法不用任何符号表示：
- 对于向量$\boldsymbol v$，我们规定$\boldsymbol v^2=\boldsymbol v \boldsymbol v=||\boldsymbol v||$。这是内积的定义。
- 然后我们“强行”把外积的定义也搬进来：对于相互垂直的向量$\boldsymbol u$与$\boldsymbol v$，我们规定$\boldsymbol u \boldsymbol v = -\boldsymbol v \boldsymbol u$。
- 我们再规定这种乘法的结合律、左右分配律对任意k-向量$\boldsymbol A$、$\boldsymbol B$都成立：$(\boldsymbol A \boldsymbol B) \boldsymbol C = \boldsymbol A (\boldsymbol B \boldsymbol C) $，$(\boldsymbol A+ \boldsymbol B) \boldsymbol C = \boldsymbol A \boldsymbol C +\boldsymbol B \boldsymbol C $，$\boldsymbol A( \boldsymbol B+ \boldsymbol C) = \boldsymbol A \boldsymbol B +\boldsymbol A \boldsymbol C $。
这个新的乘法就是几何积。为了统一，我们规定标量是0-向量。
四维世界（七）：电磁学
/** 这篇文章我打算专注一下四维世界（四维空间+一维时间=五维时空）里的物理学——电磁学。这些都是假设这个世界也符合我们世界中的一些物理规律的理论推导。虽然它电磁学不像牛顿力学那么容易让人接受，但这个类比也是无瑕兹而且很自然的（你也可以认为一切都是扯淡）。我们不讨论量子力学等其他物理，因为它们在四维空间中的推广有严重问题。 **/
在我们的三维世界，最神奇的东西之一就是电磁场了，各种电磁感应现象都是立体的，还要用到空间里的右手定则，能不能把这些东西类比到四维空间呢？当然可以。读者只要学过中学物理即可阅读除最后一节外的所有内容，如果知道大学物理和经典的不涉及相对论的麦克斯韦方程就可以全文阅读（我们本文也只考虑四维空间中的低速的非相对论物理过程，其实相对论也能推广到五维时空），其实不清楚也没关系，我会带着大家先过一遍（物理复习-_-）。我们先从最简单的两个相距为$r$的静电荷受的力说起吧。
目录
- 静电场
- 电流
- 恒定磁场
- 从安培力与洛伦兹力入手
- 磁偶极子与指南针
- 四维版麦克斯韦方程？
- 四维波动光学
Minecraft4D 教程
（这篇文章只是一个教程，所以没放进四维世界系列）
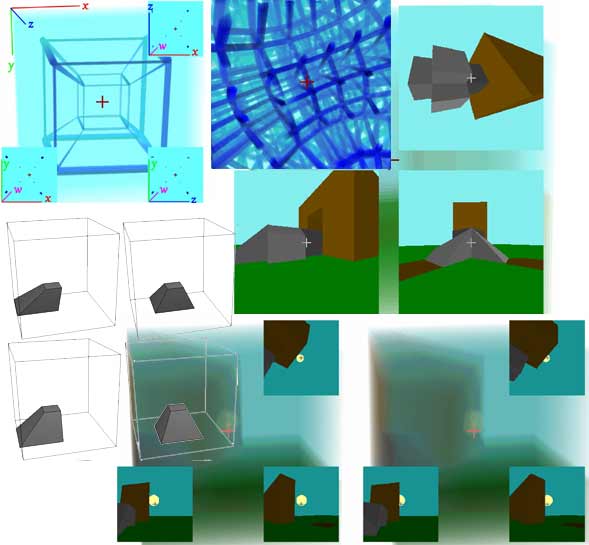
Minecraft4D是一个真正的四维空间中的（超立方体）方块沙盒游戏。（如果把时间也算上，就是五维时空！）现在游戏只支持创造模式下的单人游戏。Minecraft4D采用Javascript与Webgl编写，所以只需点开下面的链接就可以玩了。（最好用Google Chrome浏览器，不保证其他浏览器的兼容性，需要使用电脑键盘操作）
Minecraft4D
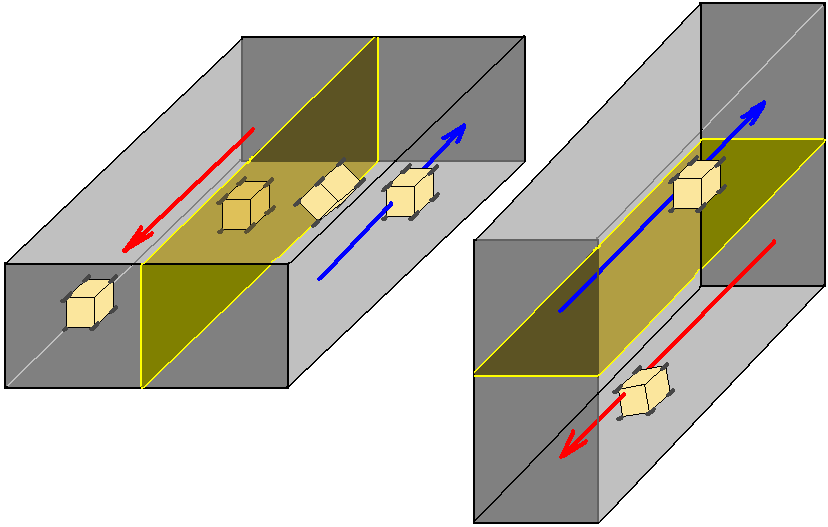
进入后等待贴图与地形都加载好后就可以看到视野了。你会发现画面分成了几乎一样的左右两个，它们是左右眼的成像用来产生双眼立体视觉，我不会做VR，所以就只有要求你要会做对对眼（斗鸡眼）来看到立体视野画面。如果做不到的话就只有通过按方向键旋转视野以得到立体感了。这篇文章里有详细介绍怎么看这种三维的画面。角落处三个小视图分别是立体视野的截面，单独抽出来以便我们清楚观察。
四维世界（六）：牛顿力学
这个系列一直都在设想一个虚构的四维世界。无论我们怎样用语言描述它的样子，缺乏物理学的世界都是静态的不能交互的。所以今天我们来学习一下这个世界里的牛顿力学。这个世界的构建理念就是要尽可能接近我们的真实世界，只是在维度上不同，所以我们全盘照搬三维世界中的理论就行了。仿照三维的游戏物理引擎我们也能写一个四维物理引擎。比如Marc ten Bosch的4D Toys就相当不错，但游戏里只能固定移动截胞(2024更新：貌似后面作者加入了旋转截面功能)，且不能自定义场景，所以我又自己造轮子写了一个。
先睹为快
如果你还不知道什么是3D视野的话，请先看教程再回来哦：
这里有很多四维物理场景（以后可能还会增加），你可以自由旋转角度观察场景。但遗憾的是除了可以按鼠标右键发射超球炮弹之外，我没想出更好的与物体交互的方法。（最好看后面的讲解获得更好的体验哦）
|
|
|
|
| 
四维齿轮（控制面板可调转速） |
四维世界（四）：二维生物视觉
很多文学影视作品里都提及过虚拟的二维平面世界以及其中的生物，因为大家很关注维度变化带来的各种效应，比如物理定律、生物和机械结构设计等。今天我们来看看大家比较忽视的一点，就是二维生物的视觉。我们不停留在描述的层面，而是通过电脑的帮助来真切体验平面生物的第一人称视角。当然我们关心二维人的体验是为了给理解四维生物的视觉做铺垫。
二维生物的眼睛
首先我们假设一个二维的世界。这是一个圆形星球，星球上住着二维人。它们的眼睛和我们的一样是通过感受光线来看到物体的。我们假设二维世界也有电磁波（这是可以存在的！只是电场是矢量，而磁场是个标量），我们只会考虑几何光学。光线从哪里发出？当然是通过这个世界中的恒星太阳与其他人造光源发出，注意所有的光线都只能在平面世界内传播。所以我们最常见的笑脸表情可不是一种二维生物——因为笑脸表情的眼睛长在脑子里，接受不到任何光线！嘴巴也在头里面，吃不到东西！所以二维生物的眼睛应该是长在头的表面的。它们眼睛的感光层是一条一维的曲线段，所以它们看到的画面是一维的。