注:这篇文章不需要读者有专业的拓扑学基础,可能一听到“代数”就给人一种抽象难以理解的感觉,因此本文更多希望从直觉上让大家感受一下代数拓扑中的同伦、同调是什么,具体正式定义和技术细节可以在任意一本代数拓扑的书上找到哦。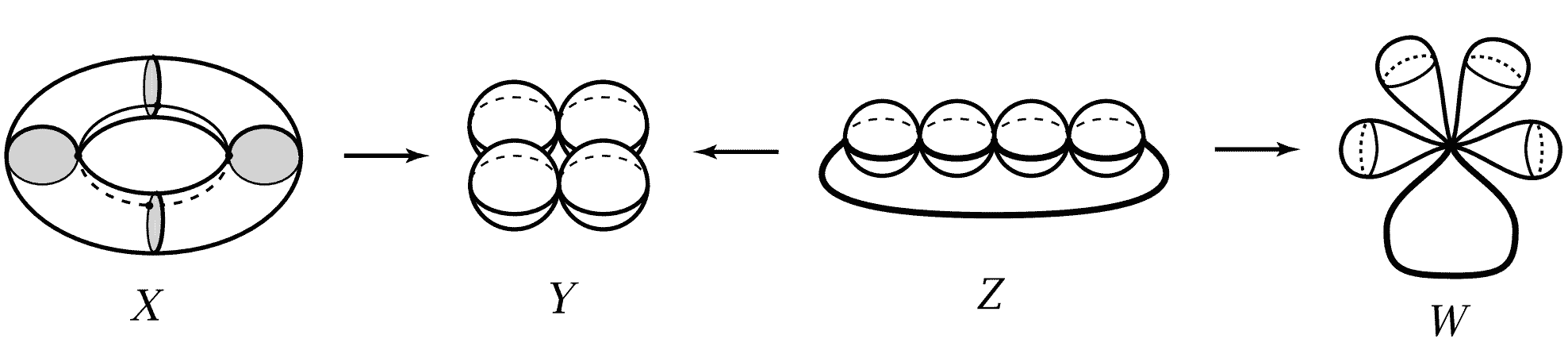
目录
我们在《四维空间(十):扭结与环扣》中曾介绍过四维空间中各种有洞的图形。怎样研究区分这些洞是拓扑学中一个重要的问题。如果您对拓扑学同胚、同痕一点都不了解的话,我们先简单说说这些基础拓扑学概念。已经了解的小伙伴可以直接跳过哦。
拓扑学简介
拓扑学不关心几何图形的具体尺寸形状,它只关心图形的连接方式,第一层直观的解释就是只要在不扯破或粘连的情况下任意拉扯图形,在拓扑学家的眼里图形就算做完全相同的。太通俗的表述肯定会损失一些细节,这里再说说第二层的解释:两个图形拓扑等价(术语:同胚)的条件是两边图形之间每个点都有一一对应的映射关系,并且映射是连续的。
这里值得注意的是,看似第一层与第二层的表述是一致的,但如果想将一个线头线尾粘起来的扭结解开,我们不得不把线剪断解开后再粘上,而第二层表述中并不需要两个图形之间整个的运动过程保持连续,只要两个状态之间能连续对应上就行,所以以第二层的逻辑看扭结与圆等价,第一层看却不等价。这里我们要习惯一个有一点反直觉的概念:当研究拓扑图形的时候,我们默认只研究这个图形本身,而不去管这个图形所处的外部空间,这样两个图形拓扑等价就叫做“同胚”,而说研究“拓扑空间”一般也指的是图形自身,而不是图形所在的外部空间。但有时确实也需要关注图形所处的空间(比如扭结只在三维空间中打结,四维及以上空间直接散架解开),这时我们要求前后图形要连所处的空间一起做连续映射,我们说三叶扭结与圆周在三维空间中不“同痕”但在四维空间中“同痕”;相对于第一层,第二层的表述还可以处理一些涉及到极限与无穷的东西,这些东西很难直观“形变”得到。下面看几个例子:
- 把圆对应到断开的圆时,开口处有跳跃,这种不连续性是拓扑学不允许的,因此圆周与圆弧不同胚;
- 字母O与字母Q的形状不同胚,因为Q的尾巴如果映射到O上一点,则O上那一个点对应Q尾巴上的所有点,不满足一一对应关系,如果Q的尾巴映射到O上的一小段弧,那它跟Q的圈重合了,也不满足一一映射要求。
- 任意开区间$(a,b)$与直线(可理解为实数轴$\mathbb{R}$)同胚,因为函数$f(x)=tan(x)$把区间$(-\pi/2,\pi/2)$中的点一一映射到$(-\infty,\infty)$,而反正切函数值也是唯一的,满足一一对应条件。对于其它任意开区间$(a,b)$显然能够通过缩放平移到区间$(-\pi/2,\pi/2)$。注意,闭区间$[a,b]$不与直线同胚,因为闭区间包含端点$a$与$b$,它们在直线上找不到对应的点。
- 平面与挖掉一点的球面同胚。我们可以通过球极投影映射构造这个同胚:除了北极点外,球面上任何一点都能唯一地投影到南极点的切平面上。
可能刚接触到平面与挖掉一点的球面同胚、任意开区间与直线同胚这种无穷大的图形跟有限的图形同胚感觉有点抽象,但接触多后慢慢它们也能变成你直觉的一部分,其实拓扑学很多看似不符合直觉的地方多思考一下又会觉得符合直觉了,在我们学习的过程中,直觉是在不断进化的。
最后我们再讲一下连通与路径连通的概念。如果一个图形可以分成多个开集的并,且每个开集之间都不相交,则不连通,否则连通。直观上就是整个图形连在一起就是连通,或者说图形中任意两点之间都有条图形中的路径相连。看似这两种描述应该是相等的,但直觉遇到无穷有时候会失灵,存在是连通但不路径连通的“病态”图形,本文就不管它们了,我们只考虑那些正常一点的空间,比如球面是连通的,因为球面上任意两点就能找到圆弧连起来;整数集不连通,因为整数集由很多孤立的点组成。我们把不连通图形中的每个连通的部分叫图形的连通分支。
我们将介绍同伦与同调(限于篇幅,下一篇文章讲同调),它们都是通过构造一些代数结构的方式来刻画拓扑空间的“洞”的工具。下面我们就来切入正题——同伦。
路径同伦与同伦基本群
怎样定义“洞”的概念呢?先看看二维情形吧。下面的图形中分别有一、二、三个孔,很简单,不是吗?
然而三维空间中像甜甜圈的圆环面$T^2$是没有边界的封闭曲面,直观上它确实有一个孔,这种孔怎样来描述呢?在《四维空间(十):扭结与环扣》这篇文章中,我们说圆环面$T^2$这种洞是一维的,因为一维的线可以从中穿过,而上图二维区域的洞是0维的,因为里面只能包裹住一个点。之前的这个思路其实在拓扑学的研究中并不太好:空心的圆周$S^1$明显有一个孔,如果放在二维空间中,孔里面只能放下零维点,放在三维空间中可以穿过一条直线,四维空间中则能穿过一张平面。我们的研究不应该取决于拓扑图形的外部空间,应该取决于拓扑空间自身。与其在外部空间用图形穿过这些孔,不如在空间内部画图形去“包住”孔。比如下图上下两行对应的图形是同胚的,从第一行可以看到由左至右分别是0、1、2维面穿过孔,但通过第二行我们明显看到可以分别用2、1、0维的图形去“包裹”孔:左图为一张球面可以包住汽泡,中图为一个圆圈可以拴在圆周的孔上,右图为两个点可以分别限制在两个不连通的区域中。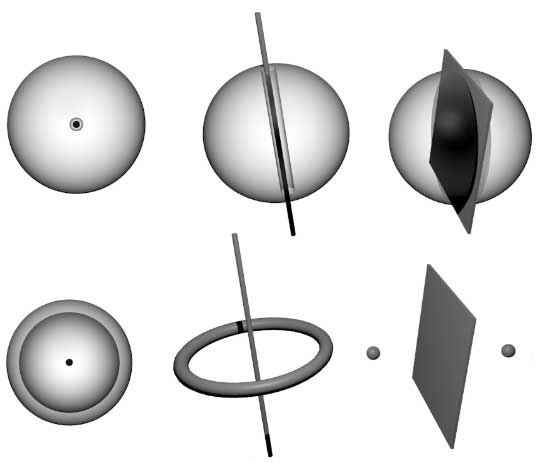
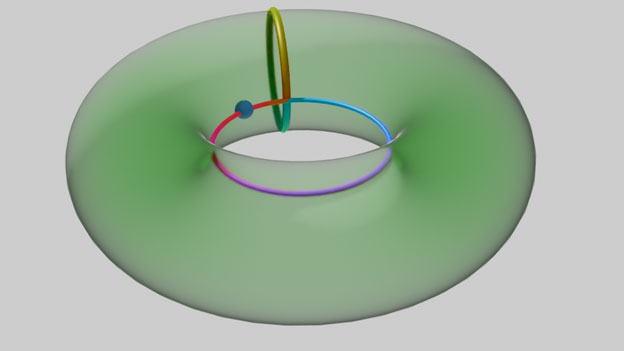
使用拓扑空间内部的图形不依赖于外部空间的另一个好处是,它让孔的定义更加清楚。直观上圆环面$T^2$只有一个孔,其实它有两个孔,分别对应下面的蓝色、红色经纬圈。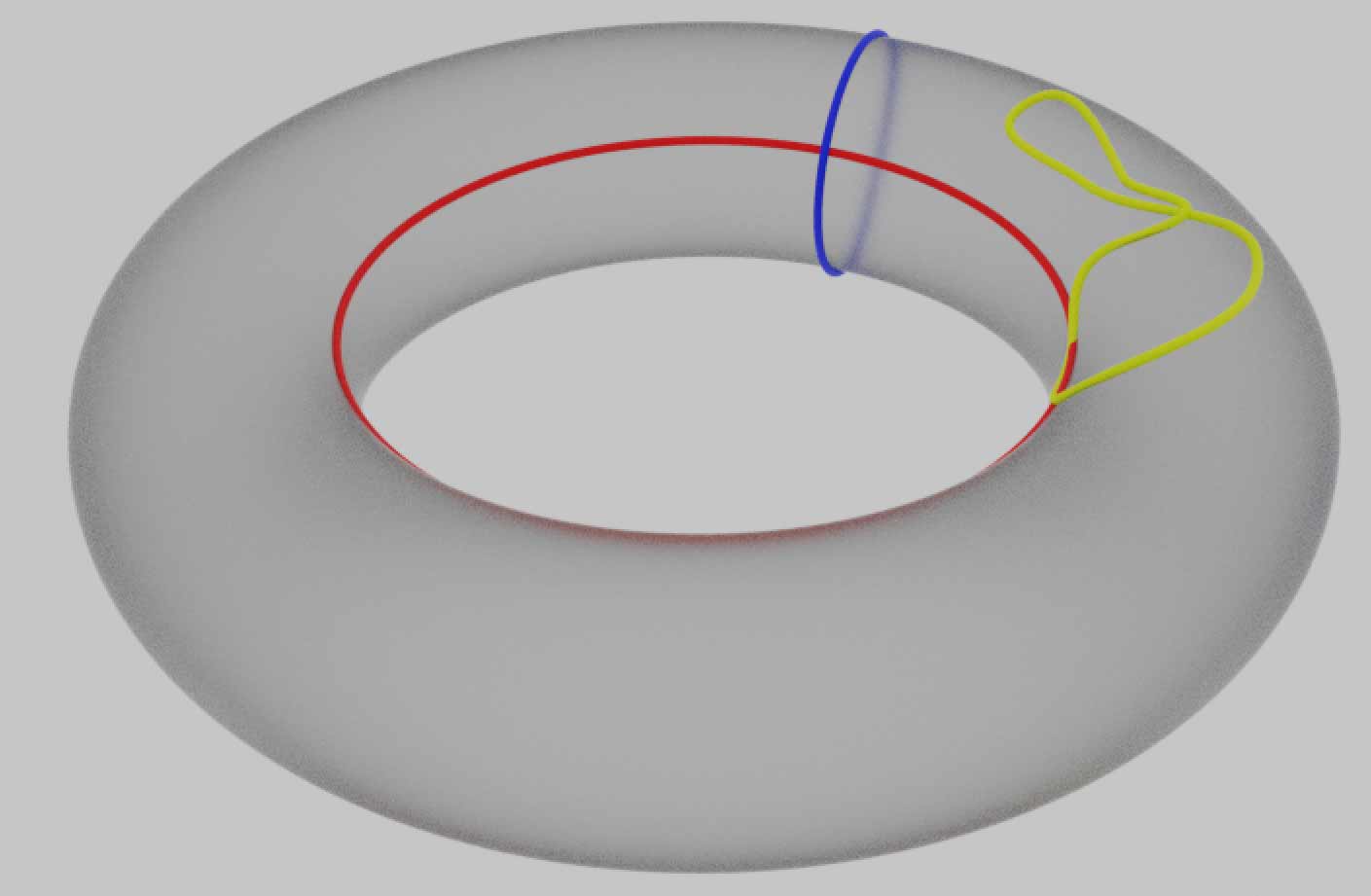
纬线红圈拴住的直接就是圆环中间的那个洞,环面由中空的圆周旋转而成,因此经线蓝圈其实还拴住了一个洞。直观上看,没被孔拴住的图形(如上图黄色圈)可以在图形中内自由连续形变缩成一个点,而被孔拴住了的图形是无法连续收缩到一点的。再次强调一下,这里的自由移动都指的是在图形中的空间中进行,这里的图形只是圆环的表面,因此路径不能画到环面以外的其它区域,即不能脱离环面画到环面内部或外部的三维空间中。如果要研究的图形是一个实心轮胎形状的三维区域的话圆圈才可以进入内部,这样蓝色圈对应的孔被填掉了(蓝色圈因此变得可缩成一点),只剩下红色圈对应的一个孔了。
现在我们虽然能找到一些套住孔的圈,但同一个孔上可以画出很多具体形状与圈数都不同的路径圈,要想研究清楚,自然就需要判断两个圈在某种意义上是否描述的同一个孔,即建立起路径圈之间的某种等价关系。下面引入路径同伦等价的概念:如果一个路径能够在图形内连续形变成另一个路径,我们就认为它们同伦等价。注意这些路径一般虽然都是圆圈,但我们只关注路径怎样在曲面上缠绕,并不关心路径自身的相交情况,因此更合适的说法是,这些封闭的路径圈是标准圆周到我们要研究的图形上的连续映射,多个点可以映射到同一点,因此路径出现自相交、哪怕迂回或缩成一点都是可以的。同伦等价的准确定义其实是这些映射之间能够连续变化的等价关系。可缩成一点的路径很无聊,那些无法缩成一点的路径才会提供有价值的拓扑信息,比如圆环上的纬线圈与经线圈。我们自然会想环面上所有路径的同伦等价类是什么样的,除了经线、纬线圈有没有其它不可缩的路径圈呢?我们可以从这两个圈出发试着构造出更复杂的路径。比如绕纬线两周,或先绕纬线一圈,再绕经线一圈,复合得到一个更大的路径。
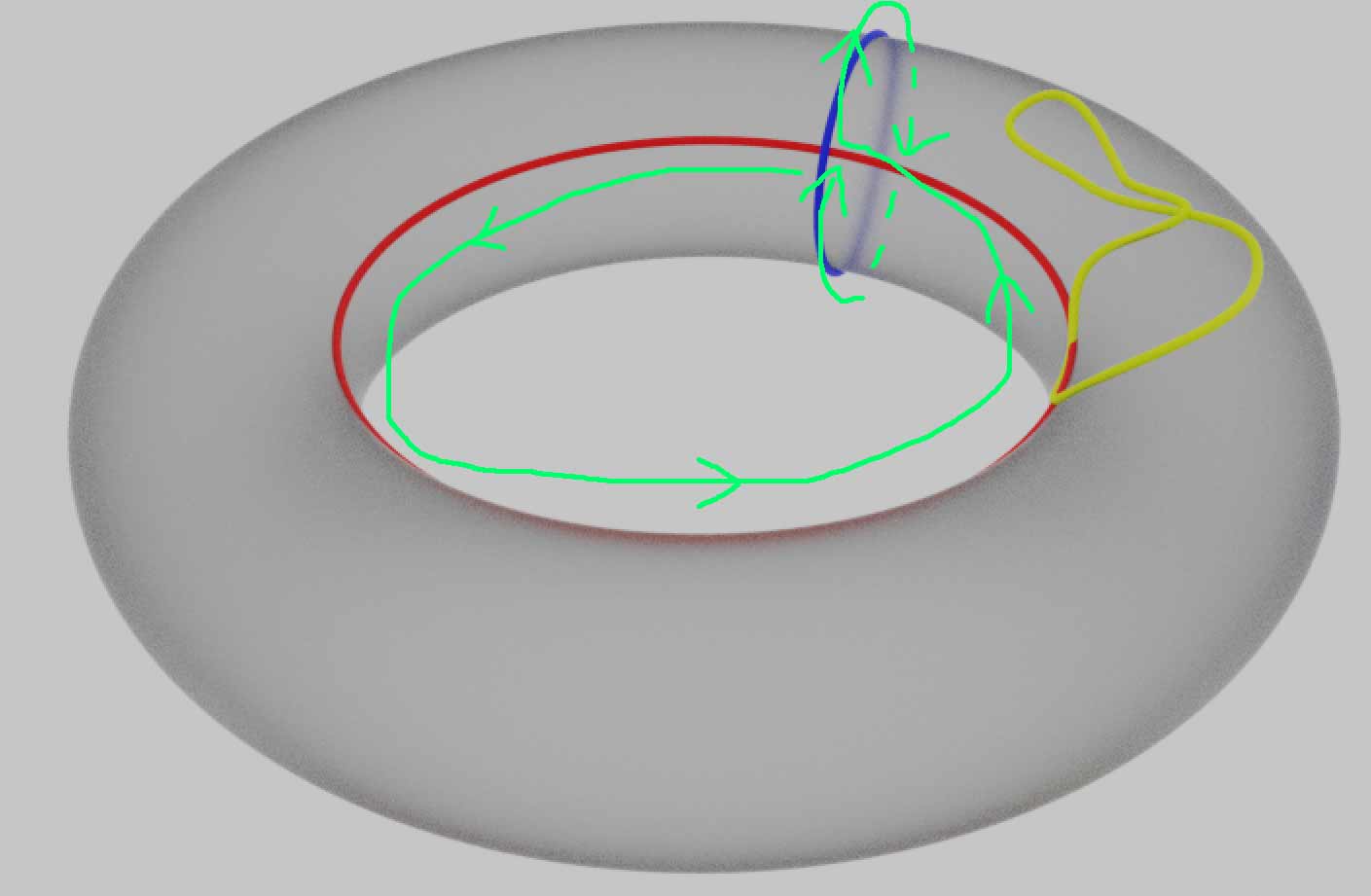
这些等价的圈之间只要通过了一个公共的点就似乎可以定义一种“加法”运算:我们走完一圈路径回到公共点后接着再走另一个路径,接起来形成一个更大的圈。注意路径本质上是映射,它是有方向的,我们不妨定义加法的逆运算——减法:只要我们逆着原来的路径倒着走回去就会抵消掉一个圈,而那些可以缩成一点的路径相当于加法中的“0”:任意增加一个这样的路径跟没增加是一样的,我们说可缩成一点的路径是“零伦”的,记作$a + 0 = a$。注意,只要处在图形的同一个道路连通分支内的零伦路径之间都是同伦等价的。
所有从同一个定点出发的路径圈的同伦等价类之间通过加法运算形成了一种叫同伦基本群(或简称基本群)的代数结构。注意这里多了一个要从同一定点出发的要求(如上图的点P),这比一般同伦的要求要强,我们称之为“定端同伦”,后面我们讨论的加法运算都是针对定端同伦。可以证明圆环上的所有过定点的路径在定端同伦等价的意义上都能通过经纬线之间的加减法得到。这个加法满足交换律:只需展示$a+b$与$b+a$之间能够连续形变。这里通过颜色展示与圆周的映射关系。我们以红橙黄绿青蓝紫的顺序映射圆周,则下图表示经线+纬线,沿纬线连续移动经线一周,路径最终变成纬线+经线。



环面经纬线之间的加法是满足交换律的,但对于一般的同伦路径间却不一定,一般来说同伦基本群是不满足交换律的代数结构。比如下面这个有两个孔的图形,很显然过点P有两个不同伦等价的圈。可以证明这两个圈的加法是不满足交换律的,下面两条路径并不是定端同伦等价。注意一般选择不同位置上的定点并不影响同伦基本群的代数结构,因为定点可以拖着路径在同一个连通分支内变化连续到另外的位置,所以我们不用纠结定点位置的选择。
拓扑空间之间的同伦
其实拓扑等价的第一层解释说不扯破或粘连的情况下任意拉扯图形,然而在这个宽泛的要求下可能仅仅是同伦而不是同胚。比如字母Q与字母O是不同胚的,因为Q的尾巴跟圆圈的交点是一个三分叉点,但字母O上找不到这样的点。但根据“只要不扯破不粘连”的原则,我们完全可以让Q的小尾巴不断缩短,最后缩到O上的一点,它们在某种意义上是等价的。然而同胚不允许字母O长出尾巴,因为O中找不到点可以一一映射到尾巴上的点。下面引入形变收缩核与同伦等价的概念:如果一个图形在“不扯破不粘连”的前提下能够在自身内部连续形变到图形中的某个子区域,那么这个子区域就是原图形的形变收缩核。图形形变收缩前后是同伦等价的,也不会改变基本群。
再比如,环面$T^2$加上四个圆盘的图形同伦等价于四个球与一个圆周粘到一点的图形。
注意,同胚一定推出同伦,但同伦不一定同胚,这里摘抄一段一个拓扑学教材中给的有趣例子:如果把阿拉伯数字0-9的形状看成平面上的一维图形,那么,按同胚对数字可分5类:{0}{12357}{4}{69}{8},但按同伦分仅有3类{12357}{0469}{8}。
那些与一个点同伦的图形叫做“可缩”的,它们相当于是同伦意义下最简单的图形了。比如所有没孔洞的实心多面体、球体,它们的形变收缩核就是一个点。下面的这个像两层纸箱子或房间的图形也是可缩的,你能想象出来它缩成一个点的过程吗?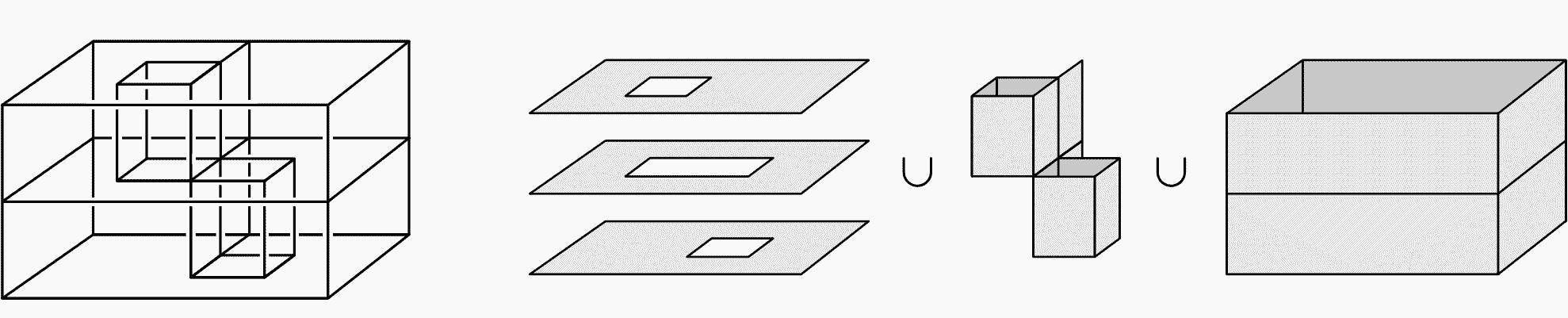
其实这两层“房间”可以由实心长方体连续形变得到:想象从实心立方体上表面挖一个竖井,直接挖到下半部分把下层内部全部挖空,然后同样,从实心立方体下表面再挖一个洞,直接挖到上半部分把上层内部挖空,两次挖掘没有相互挖穿,它们之前隔了一些面,正好就得到这个图形。实心立方体(它同胚于实心球体$D^3$)是可缩的,所以这个图形也是可缩的。看来复杂图形单靠眼睛看是不行的。
Van Kampen定理与同伦基本群的计算
之前说到,环面上的经纬线之间的加法有交换律,而二维区域分别绕两个孔的路径之间的加法没有交换律。下面我们用群论的语言来说说这两个基本群的结构。群论的基本概念很简单,就是定义了一种满足封闭性、结合性、存在单位元与逆元的运算的集合,详见《群论系列(一):群论简介》。注意之前用的加法表示路径复合,后面我们变一下写成乘法:$a^n$代表$n$个路径$a$的复合,$a^{-1}$代表相反的路径$-a$,可缩的圈(加法里单位元0)这里写成了1(乘法单位元),仅换一套记号而已,不影响数学本质。
环面与带两孔的二维区域都是以两个基本路径a、b作为同伦基本群的生成元,即所有其它路径都能由它们复合得到。对于环面生成元之间有交换律条件$ab=ba$,环面中所有的路径都能写作$a^mb^n(m,n\in \mathbb{Z})$(提示:$\mathbb{Z}$是整数集哦),这里的m与n显然是绕经纬线的圈数。环面的基本群是满足交换律的,它的Cayley图(它反映从生成元怎样得到整个群)是二维的网格,其横纵坐标值就是经纬线分别的圈数,这个群记作$\mathbb{Z}\times \mathbb{Z}$。还记得满足交换律的直积图形吗(这里讲过),其实两个群$A$、$B$之间也能做直积运算:用小写字母$a$、$b$记群$A$、$B$里各自的元素,则直积群中每个元素都是$(a,b)$这样的有序对,乘法法则为:$(a_1,b_1)(a_2,b_2)=(a_1a_2,b_1b_2)$。其实直积形的基本群正是基本群的直积!圆周的基本群是整数加法群,所以环面基本群是两个整数加法群的直积。
对于下图所示的有两个孔的二维区域,两个路径生成元之间没有任何相消的条件,也就是说,除了倒着走可抵消一个圈(即$a^{-1}a=b^{-1}b=aa^{-1}=bb^{-1}=1$)这种基本规则外,路径复合的顺序只要不相同都是不同伦的圈,因此所有可能的路径组合方式组合下来都是不同的群元素,这是一种由两条路径能生成得到包含元素最多的群,数学家干脆就叫它自由群,记作$\mathbb{Z}*\mathbb{Z}$。这个自由群的Cayley图画出来是一个分形。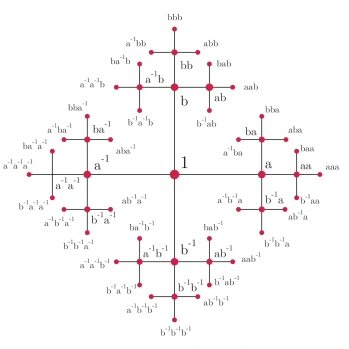
圆环跟有两个孔的二维区域两个图形基本群的唯一区别就是相差一个限制条件$ab=ba$,既然只有这一点点不同,说明它们之间应该有某种联系。如下图所示,挖掉一个点的环面它与两个共一点的圆周(即“8”字形)同伦,这个图形正是有两个孔的二维区域的形变收缩核,我们将马上看到挖孔对交换律成立与否有重要影响。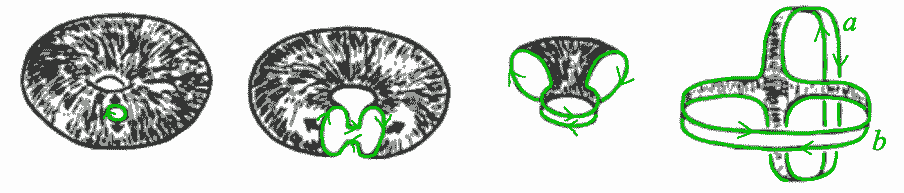
环面挖掉一个孔后将导致图中本来可缩的绿色路径不再可缩,同伦等价到两共点圆周(分别记为$a$与$b$)这个图形中,绿色路径为$aba^{-1}b^{-1}$。我们换一个角度来看:两共点圆周正是二维区域挖去两个孔图形的形变收缩核,它的基本群我们早已讨论过是由两个路径a、b自由生成的,但一旦我们把孔堵上(即粘上一块能覆盖住孔的圆片),绿色的路径在整个图形上就变得可缩了,即$aba^{-1}b^{-1}=1$,移下项就得到$ab=ba$,把孔“堵上”后会让不可缩的路径减少,我们记作$\langle a,b|ab=ba\rangle$,相对于自由群它有了可交换的限制条件变得不再“自由”了。如果读者了解群同构第一基本定理的话就知道群$\mathbb{Z}\times\mathbb{Z}$正是自由群$\mathbb{Z}*\mathbb{Z}$中把$aba^{-1}b^{-1}$映射到1得到的商群,其实几乎所有常见的离散群都有生成元表示法,它们都同构于某个自由群的子群。
这个把圆环分为堵孔的圆片和剩下的同伦于两个共点圆周的例子启发我们,计算复杂图形的同伦基本群或许可以将图形分成几部分计算,再合成整个图形的基本群。Van Kampen定理说,如果一个图形可表示为两个子图形的并集,且它们的交集是路径连通的,则我们可以从两个子图形的基本群通过一种“自由积”再约去一些限制条件(即构造商群)得到整个图形的基本群。群$A$与群$B$的自由积记作$A*B$,它是什么呢?跟自由群有点像,就是指通过两个群构造一个更大的群,其中来自不同群的元素之间不满足交换律,也没有任何化简的方法。但由于两图形公存在共部分,这上面的不可缩路径可以作为“桥梁”去化简两边的一些本来是不可缩的圈,比如之前的开孔环面与堵孔的圆形补丁的交集的形变收缩核就是那个绿色圈,由于绿色圈在圆形补丁上可缩,导致它在整个图形上可缩了。我们来实战一下计算三维空间$\mathbb{R}^3$中一个圆周、两个相离圆周、两个相扣圆周、一个圆环扭结的补空间的同伦基本群。注:补空间即在全空间(这里是三维空间$\mathbb{R}^3$)中挖掉原图形后剩下的部分。
先来看圆周补空间的形变收缩核,它等价于球面再穿一根线,更进一步变形可得到球与圆周共点的图形(这种通过共点粘合构造新图形的方式叫做单点并)。我们将该图形分为球与圆周两部分。球面上所有路径都可缩,圆周上的路径可以绕n圈,它们公共部分是一个点,球面的加入并不会增加新的不可缩的圈,所以整个图形与圆周的同伦基本群相同,都同构于整数加法群$\mathbb{Z}$。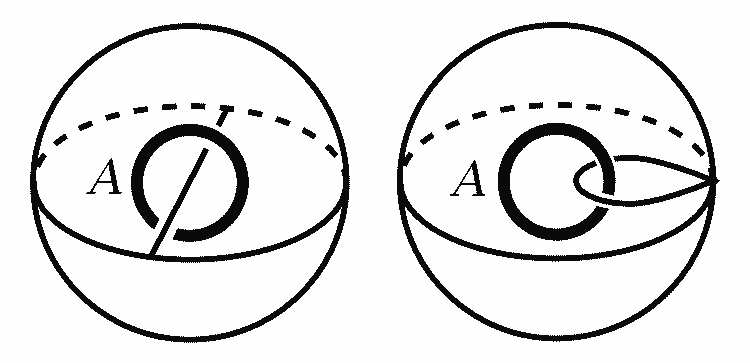
两个相离的圆周的补空间其实可以看成是两个上面的单个圆周的补空间的并集,它们相交于中间的一张平面,平面也是可缩成点的,所以整个空间是两球与两圆周的单点并。球面上没有不可缩的路径,所以只有绕两边圆环的路径,它们之间也没有可以相消的其它条件,得到二元自由群$Z*Z$。
对于相扣的圆周,它们之间可以用一个环面来分离,这可能有点难以想象,但如果我们放到三维球面Hopf纤维丛的球极投影中事情就清楚了:两个相扣的圆周正好对应二维球面上的南北极点,而任意分离它们的纬线圈对应到三维球面上正好组成环面,这些环面在《维度:数学漫步》的第八集有出现过哦。既然是环面,则它的同伦基本群是$Z^2=Z\times Z$。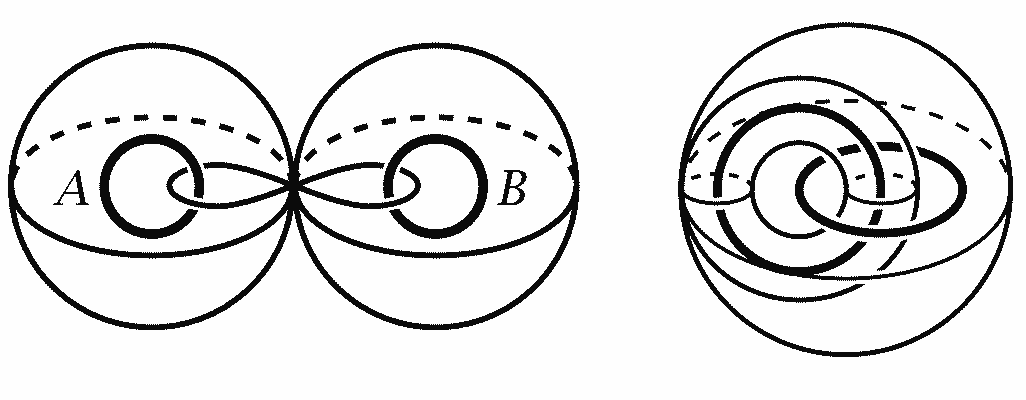
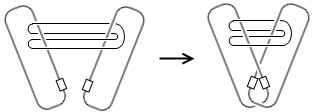
我们看到相离圆周的补空间的基本群大于相扣圆周的基本群,即把圆周扣上后有些不可缩的路径会变得可缩。Matrix67的博文中提到过一个有趣的数学小魔术正好就反映了这两个同伦群的差别:
于是,一个小魔术就诞生了。像下图中的左图那样,把一根细线圈缠绕在两个别针上,容易验证这个线圈是取不出来的。现在,把两个别针别在一起,线圈就奇迹般地自己脱落出来了。(你能看出来吗?)
注意这三个例子形变收缩核的两部分的公共部分都是一个点,不包含其它不可缩的路径,没有能化简两边路径的“桥梁”,所以整个图形直接是两个群的自由积,球面是所有路径都可缩的单连通图形,基本群只有单位元1,1跟任何群做自由积还是1。
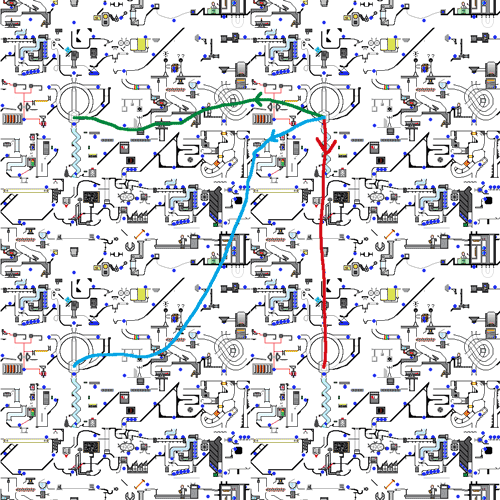
最后我们来个复杂的:计算环面p,q扭结在三维空间中的补空间的同伦基本群。何谓环面扭结呢?由于经纬圈的存在,我们可以像球面那样通过经纬坐标描述环面上的点,如果一个动点的经纬度变化速度的比值始终保持相同,则环面上就会形成一些运动轨迹,只要比值是有理数最后就能形成一个闭合的一维轨迹,这个轨迹通常都是打结的,从有理数p/q得到的扭结就叫环面扭结。比如下图左图就是一个最简单的2,3扭结(三叶结)。我们的环面也不一定要放在三维空间中,把三维空间看作是挖掉一点的超球面做球极投影得到的空间,就可以把环面和扭结都扔到超球表面上,这些图形在四维几何中有着重要意义,详见cfy的这篇文章。其实升维到超球面是有好处的。比如环面p,q扭结与q,p扭结等价是很难直接看出来的,但如果我们知道超球的球极投影能将环面经纬线对调,那么这个结论就显然了。根据孔的维度匹配,三维区域挖掉零维点形成的孔必须要二维曲面才能套得住,一维路径匹配不了,全都可缩(三维区域挖掉零维点的形变收缩核就是球面,球面上所有路径都可缩),因此我们可以放心地补上无穷远点研究超球面$S^3$上挖掉环面扭结的空间的同伦基本群,等会将看到放在超球上会简化同伦基本群计算。
环面自然把超球面分成了两个部分,一个是环面的内部区域,另一个是环面外部区域再加无穷远点(因为包含了球极投影极点),它们都是实心的三维环体,两个环体的交集就是环面。在挖去扭结的补空间中,两个环体的拓扑形状不受影响,但它们的公共部分变成了挖去扭结的环面,如上图右图所示,这个公共部分的形变收缩核跟扭结本身是一样的,都同胚于圆周。
现在有了两个环体区域与它们的交集——一个同伦于扭结的挖掉了某些区域的环面,我们就可以使用Van Kampen定理了:注意两个实心三维环体的形变收缩核也是圆周,分别对应下图中的蓝圈和红线,注意红线也是圆周,只是球极投影过了极点。圆周的基本群是整数加法群$\mathbb{Z}$,因此整个补空间的基本群就是由分别绕红、蓝圈的路径生成的自由群再除掉公共部分作为桥梁得到的一些可化简的路径,下面我们就来看两个区域之间哪些路径可以化简。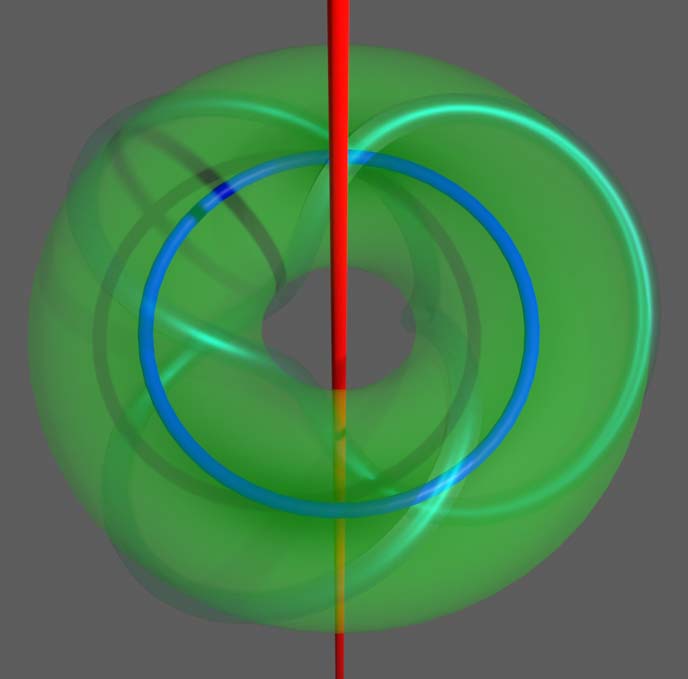
两个环体的公共部分同伦于三叶结,观察一下不难发现这个三叶结路径分别在两个环体中绕了2圈和3圈。记绕红、蓝圈的路径生成元为$a$、$b$,则公共区域作为“桥梁”,我们能得到$a^3=b^2$。这个群记作$\langle a,b|a^3=b^2\rangle$,类似地我们可以得到p,q扭结的基本群为$\langle a,b|a^p=b^q\rangle$。这些群的Cayley图有点难画,我Google了一下发现还真有人画过。
覆盖空间与道路提升
刚才一直都在跟抽象的基本群打交道,我们将看到纯几何上定义的覆盖空间与基本群之间有着一种千丝万缕的联系,其实基本群有着很强的几何意义。想象你身处一个环形过道当中,绕一圈过后你发现你并没回到原点,反而来到了一个新的地方,你一定会觉得十分诡异,就像通过传送门来到了一个新的世界;再想像你在楼道中往上走,却发现往上走又回到了原来下面的楼层,这也十分令人害怕……大家可以看一下这个B站上的视频展示了三维空间中挖掉一个传送门框的补空间的一个形成二重覆盖空间。这里吐槽一下视频作者不懂数学,标题写的非欧几何空间,其实跟非欧无关,应该叫覆盖空间才对。貌似大众认为只要不同胚于$\mathbb{R}^n$的空间都是非欧空间……
下面来看覆盖空间的定义:覆盖空间由两个空间与一个映射共同组成:覆盖空间$\tilde{X}$与底空间$X$之间存在一个连续映射,底空间$X$任意一点的领域的逆像都是覆盖空间$\tilde{X}$中不连通的很多部分,且每个连通分支都与该点领域同胚。翻译成听得懂的人话就是,底空间任何点都被覆盖空间覆盖了n层,每一层局部看起来都跟底空间是一样的。下面给几个例子:
- 无限长的螺旋线延轴线投影得到圆周,这是圆周的一个无穷层的覆盖空间。
- 观察下面这个很NB的gif动图中的球,它们跑出游戏边界就会从对面出现,这样的拓扑结构同胚于环面。因为上下左右都相连,我们可以把图片复制平铺满整个平面,图片中每件东西在这个平面中都有无数个,按照覆盖空间的定义,二维平面$\mathbb{R}^2$是环面$T^2$的一个无穷覆盖。其实这个动画只有30帧,循环播放,算上时间维,整个时空的拓扑结构是三维环面$T^3$,它是三个圆周的直积(同胚于各种圆环环曲胞),基本群是$\mathbb{Z}\times\mathbb{Z}\times\mathbb{Z}$。

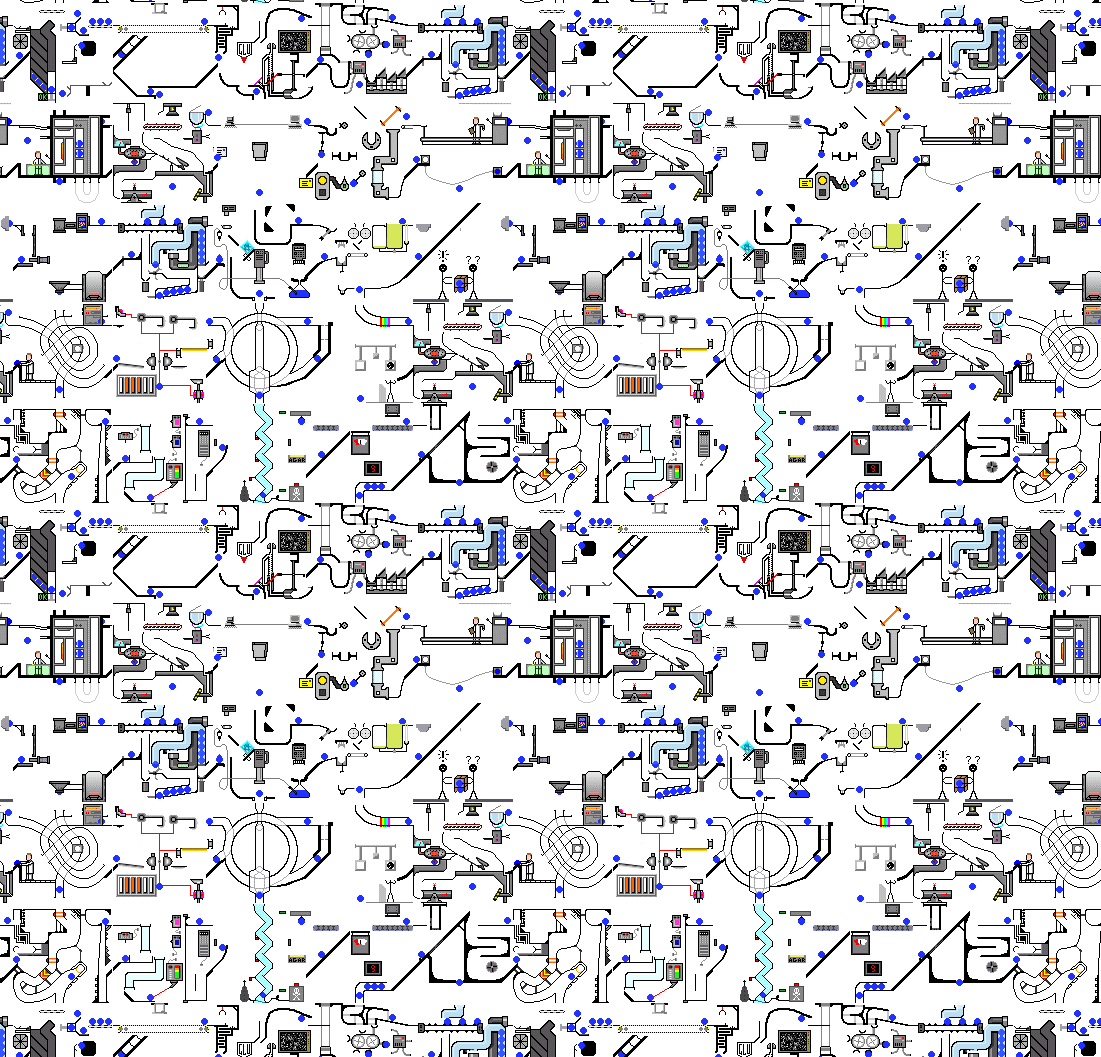
环面上的某一个环路,在覆盖空间中则对应无数个环路。但如果把环路的起点在覆盖空间中确定下来,则覆盖空间中的道路可以唯一确定,这就是覆盖空间中的道路提升的唯一性定理。底空间中环路终点跟起点是同一个点,但在覆盖空间中环路却可能是一条连接两不同点的路径。不难发现只要在覆盖空间中从一个点出发,到另一个相同对应底空间中的点,在覆盖映射到底空间后都能得到一些互不等价的不可缩的路径。其实覆盖空间满足一定条件后跟基本群可以有种一一对应的关系。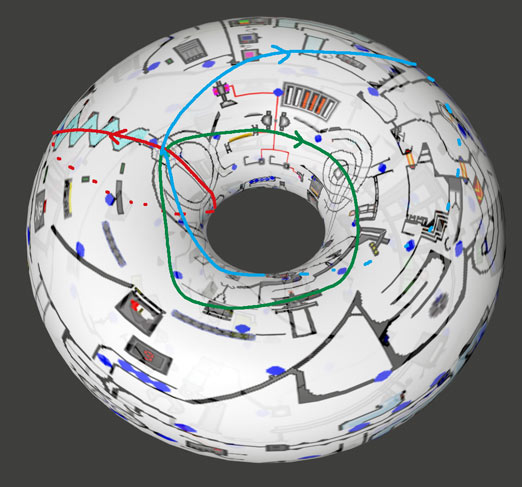
覆盖空间分类与万有覆盖空间
对于两圆周的单点并图形,它的覆盖空间是什么样的呢?我们将给出很多很多覆盖空间。这些例子来源于Allen Hatcher的代数拓扑教材。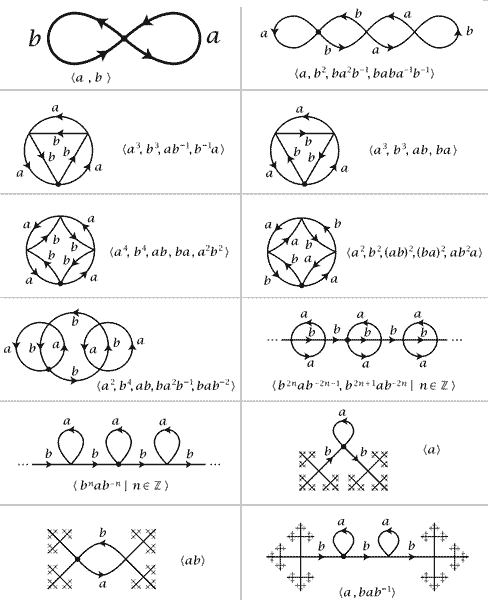
这么多覆盖空间,有没有覆盖层数最多的空间呢?试想,如果只要沿着不可缩的圈走一圈回来都会“穿越”到新的世界去,这样的空间就是最大的,我们称之为万有覆盖空间(Universal Covering Space),它可以覆盖所有其它的覆盖空间。由于万有覆盖空间中所有的不可缩路径都被提升成一条不封闭的路径了,不存在不可缩的路径了,所以万有覆盖空间是单连通的,它的基本群为1。一个图形的万有覆盖空间的形状其实非常像它基本群的Cayley图的形状,比如环面的万有覆盖空间就是之前看到的平面$\mathbb{R}^2$,两圆周的单点并的万有覆盖空间则是一个之前画过的跟两生成元的自由群Cayley图一样的完全没有环路的分形。
可以看到,覆盖空间变得越大,基本群就变得越小,其实一个空间的所有覆盖空间跟基本群的子群是一一对应的,基本群的正规子群对应的覆盖空间还具有更好的对称性……这里就不继续展开说了。
高阶同伦群简介
看过《四维空间(十):扭结与环扣》的读者就知道,高维空间中一维路径不一定能套得住所有的孔,因为孔的维数不尽相同,必须要相互匹配才能拴得住,比如我们就不能用一维的同伦基本群捕捉到三维空间挖掉一点前后的拓扑变化。因此除了从道路(圆周)得到的同伦基本群,还有球面,超球面的高维“道路”得到的高阶同伦群,这些高阶同伦群有时候特别复杂。我们来看看圆周的各阶同伦群:
首先一维同伦群就是路径的基本群,对于同伦等价类来说只有绕孔圈数的这个自由度,绕孔m圈的路径与绕孔n圈的路径复合得到的是绕孔m+n圈的路径。因此这些路径等价类间的“加法”运算跟整数的运算是一样的,我们记作$\pi_1(S^1)=\mathbb{Z}$。这里我们用$\pi_i$代表$i$维同伦群,$S^1$代表一维球面,即圆周,$\mathbb{Z}$是整数集的符号。
圆周的二维同伦群是什么呢?我们能否将二维球面映射到一维圆周上呢?或许我们把球面拉成面条就能放在圆周上了,但它是可缩的,是零伦。可以证明二维球面没法套在圆周的孔上,也就是说只有零伦映射这一个同伦等价类,我们记作$\pi_2(S^1)=0$。通过覆盖空间相关理论可推出更高维的超球面也没法往圈上套,因此圆周的大于1阶的同伦群都是仅包含单位元的平凡群。
下面我们研究一下二维球面的各阶同伦群:首先,球面作为一个没有孔的单连通图形,所有一维道路都可缩,因此一阶同伦群为0。二阶同伦群则是用球面自己来覆盖自己。回想一下一维的圆周可以覆盖自己n圈,可以证明(Hopf度数定理)$n$维球面自己覆盖自己的方式也可以用一个圈数来描述,同伦群结构也是跟整数的加法对应,记作$\pi_n(S^n)=\mathbb{Z}$。
这里要注意一下高维的球形“道路”之间怎样定义加法:将球面的赤道捏成一点,我们会得到两个球面的单点并。这个过程的逆过程就是两球面道路相加得到的新球面,由于维数更多,所以二维及以上的加法运算都可以有空间交换位置,满足交换律,但这并没有让高阶同伦群变得简单。似乎我们可以同理觉得二维球面的三维同调群也是零伦的,但例外开始来了。我们想构造一个不可缩的,将三维球面映射到二维球面的映射。还记得Hopf纤维丛吗?Hopf纤维丛中,三维球面上的每个纤维是个圆周,对应二维球面上的一个点。这正是一个非平凡的将三维球面上的点映射到二维球面的方式。可以证明这个Hopf映射是不可缩的,并且它自身还可以复合,同样可以数某种“圈数”,所以球面$S^2$的三阶同伦群也是整数加法群$\pi_3(S^2)=\mathbb{Z}$。这种“例外”多不多呢?其实高阶同伦群的复杂结构并不是例外,看看下面这张表就知道高阶同伦群有多恐怖了。$n$维球面的所有同伦群的计算其实是拓扑学中的一个至今都非常困难的问题。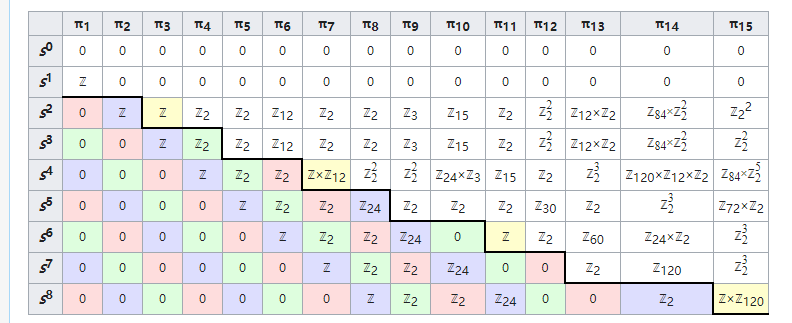
同伦群的求解是非常困难的,有没有简单点的处理方法呢?下一篇文章我们将引入一个与同伦相近的概念——同调,与同伦群不一样的是,它定义的是永远满足交换律的加法运算,计算也要相对简便。(未完待续)