一个圆环环的透视投影框架图（曲胞分段为直胞画出）
特色内容
本文目录：
双圆柱与直积形
上篇文章介绍了一种新的四维几何体:$$\begin{cases}x^2+y^2\le a^2 \\ z^2+w^2\le b^2\end{cases}$$它只有两个弯曲的三维面：$$\begin{cases}x^2+y^2= a^2 \\ z^2+w^2\le b^2\end{cases}、\begin{cases}x^2+y^2\le a^2 \\ z^2+w^2= b^2\end{cases}$$
它们的方程看上去像圆柱柱面的一部分；这两个三维面相交得到一个二维曲面，球极投影下来就是那个圆环（圆环把三维空间分成了内外两部分，对应它的两个三维表面）
看到几何体的方程组我们还是不能想象它长啥样，但能从方程看出它在面$xy$上的投影是一个半径为$a$的圆，在面$zw$上的投影是一个半径为$b$的圆。通过计算我们能得到每个投影的形状。我们可以模仿“三视图”画出它的“四视图”(三维)或“六视图”(二维)，但通过三视图来认识几何体好像也不是一个很直观的办法，四视图也不直观，我把四视图附在本文最后。反而我认为截面法比较直观，让我们像《维度》第三集那样让这个图形穿过三维空间，看看它的截面动画：
|
|
|
不知道大家有没有发现，这个圆柱体截胞的“伸缩”和一个圆穿过一条直线的动画是类似的，这说明这个这个圆柱体侧面的每条棱在四维空间中都是一个圆！给我们的感觉就是这是一个底面为圆形，侧面也是圆形的柱体。这个几何体在维基百科中叫做“Duocylinder”，我不知道正规翻译，从字面上翻译就是“双圆柱”，以后我们就暂时这样称呼它。
注意，双圆柱不是我们第一篇文章所说的“圆柱柱”。圆柱柱的截面动画很简单：一个圆柱体突然出现，过一会又突然消失；双圆柱的截面动画是一个圆柱先变长再变短。那除了截面动画，双圆柱和圆柱柱的关系和区别是什么？我们先看一类新的几何体：直积形（Duoprism）。直积形是我对它的称呼，也没有查到官方中文名称。维基百科上对直积形的定义就是：由两个多边形做直积（笛卡儿积）得到的图形。
上一篇文章里我们介绍了圆柱面是线段和圆的直积，可以看作由很多线段或很多圆拼成（圆柱体是实心圆盘和线段的直积），这两种看法说明直积有交换律。形象地说直积形就是把一个图形$A$在绝对垂直的另一个图形$B$的范围内不断平移，把能平移占满的空间(四维)都占满的图形。当然平移出来的很多线都在这个空间(四维)的内部，所以我们只在$B$的每个边线顶点处看到了图形$A$的轮廓。
我们看到的双圆柱就是两个圆的直积，而圆柱柱是一个圆和一个长方形的直积。（一般n维图形与m维图形直积得到(m+n)维图形）
由于圆是正无穷多边形，所以我们先从正多边形的直积开始说起。
返回目录
ｎ m边形-直积形
我们仔细看超立方体的投影图就会发现里面的正方形能分成绝对垂直的两类（右下图红色和蓝色部分），不仅如此，我们还能以这样的顺序画出超立方体投影图：先画一个蓝色的平行四边形（其实是正方形，视角问题），然后在每个顶点上再“复制”四份红色平行四边形；我们再选择一个红色平行四边形，在每个顶点上再“复制”剩下三份红色平行四边形。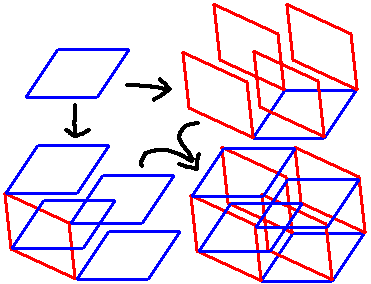
这种画法展示了超立方体像一个底面是蓝（红）色正方形，侧面母线是红（蓝）色正方形的柱体！我们现在要放开一个概念：柱体的侧面母线不一定要是一个一维图形（一条线），它完全可以是任意高维的图形。还记得第一篇文章中我们构造了一个奇怪的八棱柱柱吗？它是八边形与三角形的直积：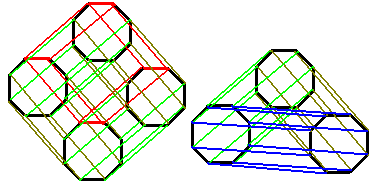
维基百科上把正m边形与正n边形的直积叫做：m n-gonal prisms（m n-多边形直积形？）当$m=4、n=\infty$时我们就得到了圆柱柱。这时有一个图形有无穷个边，我们想画出它就得平移无穷次！其实它有曲胞（曲面的类比），我们画不出曲胞的框架投影，因为它是由无数很小的平直的胞微元构成的。我们不妨画到16边形就停止。下图左边给了16-4边形直积形两个视角的投影图，我们看到第一个视角和圆柱柱确实很像，它是4个圆组成的一条带子，正方形负责链接它们对应点；第二个视角中感觉是16个正方形组成的一条带子，四个圆负责把正方形对应点串起来。这又是直积的交换律。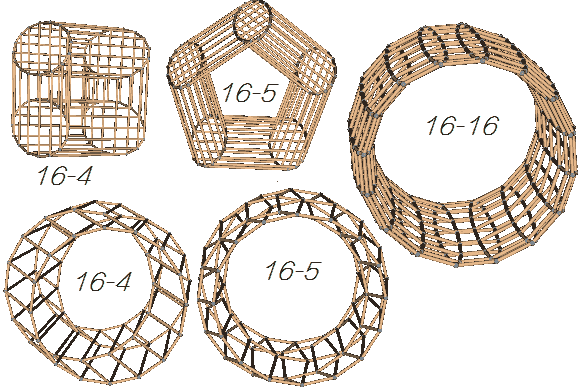
我们把正方形换成五边形、……16边形，可以看到这两个视角变得越来越像，对于16-16边形直积形来说两个图形就都一样了。
看了平行投影我们还能再看直积形的球极投影，16-16边形直积已经很像纤维丛里的那个圆环了。由于直积有交换律，我们终于可以理解圆环经纬线可交换了。(jenn3d上菜单“duoprisms”中有这些模型)
圆柱的所有四维类比
该总结一下“柱体”这个概念了。我们三维的柱体是2维底面$S$与一条线段$h$的直积，四维中传统的柱体是3维底面$V$与一条线段$H$的直积。那么“xx柱柱”就是$V\times H = S\times h \times H=S\times (h \times H)=S\times (长方形)$。所以四维圆柱类似物有四种：
- 球柱(3-球$\times$1-球)(spherinder);
- 双圆柱(2-球$\times$2-球)(duolider);
- 圆柱柱(2-球$\times$1-球$\times$1-球)(cubinder);
四维空间中的旋转
球极投影中的圆环只是一个三维的“影子”，我们看到它的实体双圆柱其实是一个没有任何孔的凸胞形。让我们回到三维圆环的定义：它是圆绕圆所在平面中的一条轴旋转而成的。
四维空间的旋转很复杂。但这里我们只需要类比：四维“球环”是球绕球所在三维空间中的一张平面旋转而成的——这就是四维旋转体。
何谓绕平面旋转？如果是“单旋转”的话，我们能够找到一个平面，它上面的所有点在旋转时不动（就像三维的旋转轴），其实n维空间中任何点旋转的轨迹都是圆，所有轨迹圆所在平面都应该平行，它们的所有圆心就构成了那个平面。
比如你把一个四维物体$(x,y,z,w)$的$x、y$坐标单独拿出来绕原点做旋转，则$xy$面就是发生旋转的面，$zw$面上的点不会动，我们说这是绕$zw$面的旋转。
既然有单旋转我们就有双旋转！还是四维物体$(x,y,z,w)$，我们让$x、y$坐标做匀速$v_1$的旋转，让$z、w$坐标做匀速$v_2$的旋转，由于它们绝对垂直，运动不会相互干扰，结果导致整个空间都在旋转，除了原点你再也找不到哪些轴或面是不动的！而那些不在坐标面上的点将参与两个旋转的叠加，这就是四维空间旋转的复杂性。
如果$x、y$坐标和$z、w$坐标旋转速度相同，则所有点旋转的轨迹还是圆，我们可以想象这个旋转将使整个四维空间充满圆周轨道，如果我们只关心单位超球上的圆周轨道，把它们球极投影下来就是Hopf纤维丛！
如果$x、y$坐标和$z、w$坐标旋转速度不同，这就是两个不相干的圆运动的合成，CFY的这篇文章有详细的图文介绍。
双旋转像纤维丛一样都是有手性的。我们用一幅图来表示一下这些旋转的关系：圆环上的四簇圆。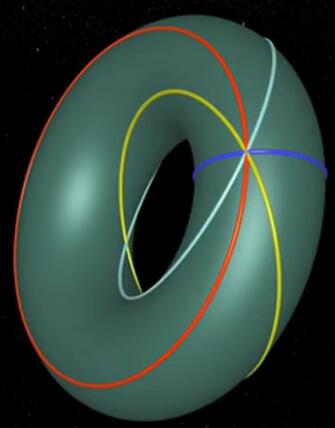
绕$xy$平面旋转一圈对应蓝色圆周，绕$zw$平面旋转一圈对应红色圆周，右手等角旋转对应黄色圆周，左手等角旋转对应白色圆周。为什么黄色圆周与白色圆周相交了？他们的交点代表$zw$平面、$xy$都旋转了180°，即四维空间中的“中心反射变换”——把任一点映成与一个原点对称的点的变换！（三维和其他奇数维空间不能通过旋转合成中心反射变换，因为做了中心反射变换后会得到镜像，但四维和其他偶数维能通过旋转得到）
非等角旋转呢？它们的旋转轨迹构成了一些扭结！由于这些旋转轨迹都在圆环面上，所以这些扭结叫做环形结。图片见CFY的这篇文章。
圆环上的圆（注意这个圆不是旋转平面与超球的交圆，因为圆环经纬线不是Hopf纤维丛的一部分）为什么能和旋转对应？我们知道圆环本来是双圆柱的球极投影，它可以用$xy$平面上的圆和$zw$平面上的圆的参数方程描述：两个分别在$xy$平面和$zw$平面上的角度，当然它就能且只能表示发生在$xy$平面和$zw$平面上的旋转，这个圆环上$xz$平面上的旋转是画不出来的。
四维空间中的旋转还可以用代数解释并推出它的很多性质，我们后面再来说。
返回目录
球环（Spheritorus）
回到圆环类比上来。球环肯定像圆环那样有洞，所以不是凸多面体，球极投影就不适合做了，对于曲胞来说线框投影也不现实了，了解几何体就只剩截面法了。我们先看看三维圆环平行于旋转轴的截面动画：
通过类比请大家想一想四维球环的平行于旋转面的截胞动画是什么样的，我会在下面给出答案。
截面动画能够完整地展示任何一个复杂的三维/四维几何体，所以按理说我们看到物体一个方向上的截面动画是能推出另一个方向上的截面动画的。现在我们换一个方向截三维的圆环——垂直于转轴的平面：你能不不能不想圆环的三维样子直接根据上面的截面动画推出下面另一个方向上的截面动画吗？
通过类比请大家想一想四维球环的垂直于旋转面的截胞动画是什么样的。
下面揭晓答案：
幸好我们有计算机能够画出这些截面：
这个图形简直就是三维圆环被平面截得截面形状的三维翻版。
观察一下我们得出：二维截面绕水平的轴旋转一圈得到的图形。二维是一个圆长大分裂成两个圆最后再合回来，三维就是一个球长大分裂成两个球最后再合回来。像不像细胞分裂？
返回目录
换一个角度
我们可以换一个方向——垂直于转轴的平面的截胞截四维的球环：
嗯，我们已经搞清球环的截面动画了。还记得圆环斜着切能切出两个Hopf圆吗？但球环好像切不出两个球，我只能找到这个图形：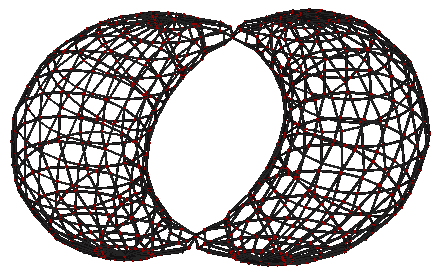
它已经不是对应圆环截面的旋转体了，感觉像是强行把截面打气鼓成三维的图形一样。
圆环的另一个类比——环球
三维圆环的截面动画视一个圆周变“粗”（变成二维圆环）再变细，四维的圆环为什么不是一个球面变“厚”（变成有厚度的空心球壳）再变薄呢？这就是圆环的另一个类比。然而我也不知道这个东西该怎么命名。
现在我们只有一个方向上这个物体的截胞$A$的截面动画，但这就足以完整描述整个几何体了。我们想想它的另一个垂直方向上的的截面动画：设新的垂直于胞$A$的胞为胞$B$。胞$B$在胞$A$中的截面是一张平面，我们先把这张平面放在一个位置，那个变“厚”变薄的球会被这张平面所截，产生了一个二维的截面动画。这个二维的截面动画就描述了胞$B$截几何体的截胞。平移这张平面的位置（其实就是在平移胞$B$），重复上述步凑得到一系列的截胞，它们连起来就是$B$方向上的截胞动画了。
不知你能否想出另一个方向上的截胞动画。
下面揭晓答案：
我对这个图形的理解是：就像四维直积形虽然不是狭义上的柱体我们也可以认为它是广义上的柱体，即侧面是一个二维图形的柱体。所以这个几何图形是一个圆“绕着球”转出来的图形，基于这点我们把这个几何体叫做“环球”（Torisphere）。前面的球环是一个球绕着圆转出来的图形，我猜它们的关系就像环面上经纬度互换那样，应该是五维直积图形$\mathbf S^3\times \mathbf S^2$在四维空间的球极投影的两个不同视角。
以上可能说得太抽象了，其实作为旋转体，它是三维圆环绕包含它对称轴的平面旋转得到的旋转体！
返回目录
圆环环
圆环的类比为什么是什么球什么转出来的，而不是圆环绕着平面旋转形成“圆环环”呢？虽然这个想法有点较真，但下面我们不妨也看一看：
圆环不像球高度对称，所以我们选择它绕平面旋转式有很多取法：
- 取垂直于圆环对称轴的平面（双圆环：Tiger，这个英文名字真奇葩）
- 取平行于圆环对称轴的平面（圆环环：Ditorus）
- 取斜着的平面
我们直接给出它们的一些截胞的形状：我们都能观察到三维圆环截面的“影子”。
- 取垂直于轴的平面
- 角度1：
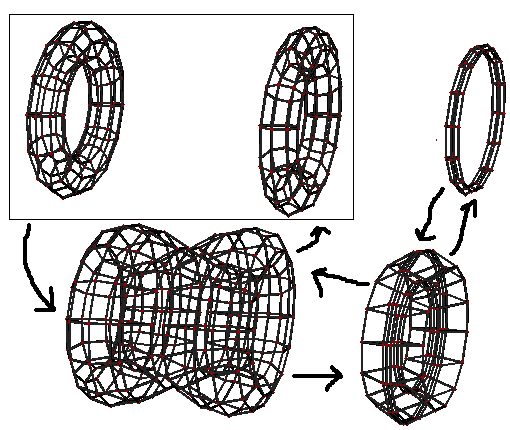
- 角度2：和角度1一样！，但它只是像长方体六个面一样，形状相似但尺寸可以不同，要看圆环环的具体参数。这说明取平行于轴的平面旋转得到的圆环有很好的对称性。其实这种对称性与双圆柱相同！因为当这个圆环无限细（变成一个圆）旋转后就变成了那个环面——双圆柱两曲胞的交面！
- 取平行于轴的平面
- 角度1：
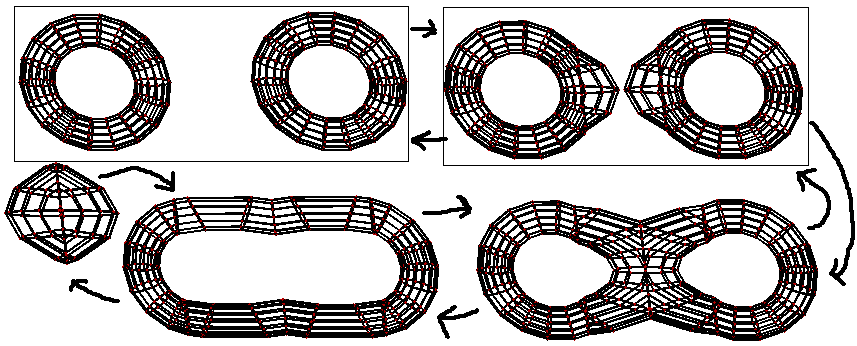
试想若平行于轴的平恰过圆环对称轴，旋转出来的几何体就是前面提到的环球了。（试想圆绕轴旋转会产生球或圆环这两种情况） - 角度2：一个圆环面先变厚再变薄。(像一个环形的水管，图略)
- 取斜着的平面
- 角度1：右下图三个太诡异了，幸好有计算机，不然我已经无法想象了。
- 角度2：左下图，一大一小俩圆环，还算规则。
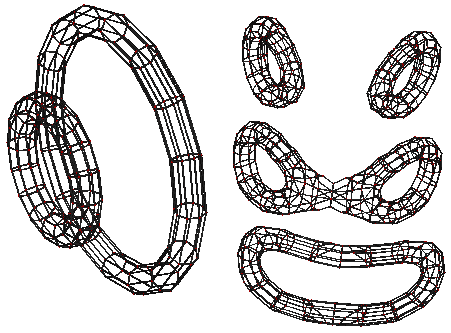
附双圆柱四视图：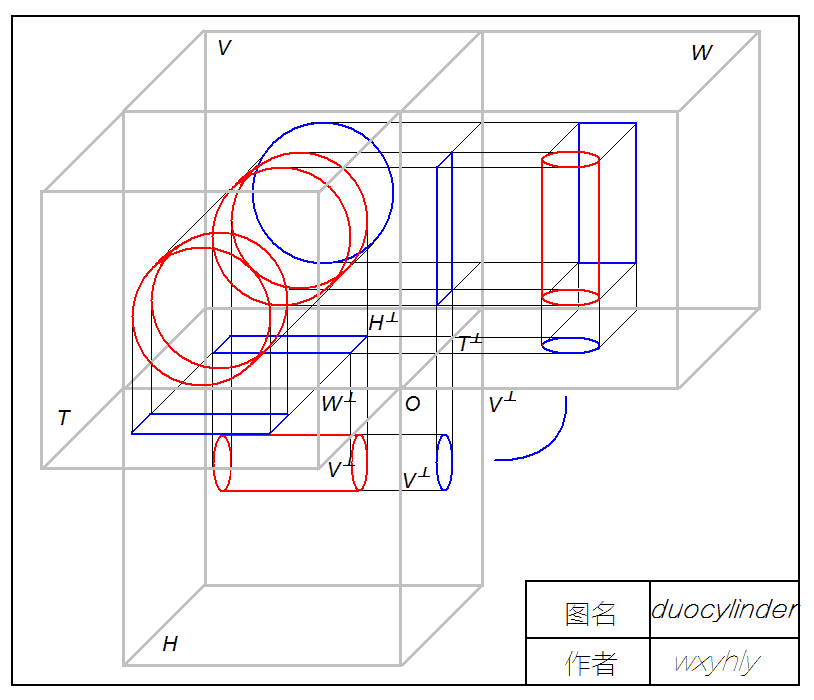
返回目录