#本文内容为对影片《维度:数学漫步》第7、8集:纤维丛的解释,并着重讨论Hopf纤维的几何性质

图片来自en.wikipedia by Niles Johnson
特色内容
- 在线webgl查看4D
- 等角平面
- 120号的大环结构
- 什么是纤维丛
本文目录:
提示:可先参看影片官网对纤维丛的详细描述
点击查看纤维丛3D模型(需要支持webgl的浏览器,如Chrome)
引子
我们先从一个很熟悉的例子开始今天的话题:坐标面$xy、zw$只在原点相交。我们曾经很努力直观想象过两无限大平面只交与一点的情景,但却怎么也想不出来,除了代数解释没有其他办法。有没有更形象的可视化方法呢?下面就有一种方法能同时可视化这两个平面的位置关系:在原点处放一个单位超球面($\mathbf S^3$),它肯定会与所有一张过原点的平面交得单位圆周。现在问题就简单了:我们通过球极投影的方法把它降维到三维空间中来直接看到那些单位圆周。
锁链
坐标面$xy、zw$只在原点相交,所以它们交单位超球产生的圆是不相交的。那它们与单位超球的两个交圆投影到三维空间的位置关系是怎样的呢?我们可以写程序画出来:两个交圆的球极投影是像锁链那样神奇地扣在一起的!这个锁链一样的图形叫“Hopf link”。
我们还想看到其它更多平面的交圆,影片中引入了复数得到的Hopf纤维丛正达到了这个目的——它让我们更好认识了四维空间中的平面(因为所有圆由过原点平面截得),也认识了超球面$\mathbf S^3$本身的精彩性质。其中,复数的引入是最精妙的地方——视频里是这样讲述的:
$z_2=k.z_1$ (有没有注意到影片中的细节:法国人的乘号像小数点,小数点像逗号)
很简单的一个式子。我们详细解释一下:先在四维空间中选任意一个平面$A$为坐标轴$z_1$(这个轴是复数的,所以是二维的),再选平面$A$的绝对垂直(因为坐标系$z_1Oz_2$正交)平面$B$为坐标轴$z_2$。比如我们就选$xy$和$zw$这对面吧,具体规定$(x,y,z,w)\to(z_1,z_2)$的计算方法(可以任意规定,这里只是图方便):
$$z_1=x+iy $$$$ z_2=z+iw$$
代入式子$z_2=k.z_1$就能得到平面满足的方程。其实式子$z_2=k.z_1$中复数的乘法在四维空间并没有明确的几何意义,我们只是借助复数很方便随意地得到了一组平面($k$取不同值就对应不同的平面),但巧就巧在它们都是两两扣在一起的!
$k$可以在扩充复平面上任取(扩充指$k$可以等于$\infty$,代表平面$z_1=0$)。我们又知道,球极投影能把球($\mathbf S^2$)映射成平面加一个无穷远点,所以我们可以认为$k$是在一个二维球面上取的点,每个$\mathbf S^2$上的点($k$的值)都对应一个超球($\mathbf S^3$)上的圆($\mathbf S^1$)。当然,这个二维球面上取$k$点存粹是Hopf想从拓扑学上构造$\mathbf S^1\to\mathbf S^3\to\mathbf S^2$的映射搞的数学把戏,它没有直接具体四维几何意义。(其实也有:两个平面的$k$值在这个$\mathbf S^2$上的球面距离正比于这两个平面的夹角,但直接证明繁琐,优雅证明可能需要从“复射影直线”上找灵感?)
不是只有球极投影
影片里有大量Hopf纤维丛的球极投影动画。其实我们还可以换一个角度来看Hopf纤维丛——用平行投影法仍然能看到它。维度四维空间上集(第3集)、本系列第一篇文章中的各种柱体、锥体都用的这种方法。平行投影不像球极投影形变扭曲那么严重,但平行投影导致很多不相交的地方看起来是相交的,导致线很乱。
点击在线查看4D模型!支持在四维空间中变换视角!(需要支持webgl的浏览器,如Chrome)
线确实很乱,但我们看到了圆周投影到三维空间有时能变成一条线段,从线段一头看过去它就缩成一个点了——我们这样又间接瞥到了平面交于一点的影子。
返回目录
等角平面
显然Hopf纤维丛没有表示出所有过原点的平面。比如面$xz$、面$yw$是永远表示不出来的。(它们与面$xy$、面$zw$上的单位圆周都有交点,不属于这个纤维丛)我们还感觉到Hopf纤维丛都有一种公共的属性。我们后面系统学习四维空间n-向量法能够算它们之间的夹角是等角的——即它们的$\theta_1=\theta_2$!这种平面的位置关系叫等角(isoclinic)。我们还可以证明和一个平面所有成同手性的等角平面的集合刚好组成一个完整的Hopf纤维丛。什么是同手性?以后会介绍到所有一般位置的两平面位置关系都能够分成像人的左右手那样的对称的两类。还记得《维度》影片中提到了Hopf圆周和它的镜像圆周吗?它们就是分别组成左右手Hopf纤维丛。
正120胞体中的大环结构
既然Hopf纤维反映了超球$\mathbf S^3$的性质,而面数很多的正多胞体又是超球的近似(想想二维是用正多边形逼近圆)。我们看看在正120胞体中能够发现什么秘密。它的基本参数有:
- 120个正十二面体胞、720个五边形面、1200条棱、600个顶点;
- 相邻胞形成的二胞角为144°.
- 分层结构见上一篇文章
前面我们说过整个正一百二十胞体能分成12个大环,每个环上10个正十二面体都是首尾相接的。为了描述清楚这些环的相对位置,我们给分层结构取一些代号:
| 分层 | 南北极 | 极圈 | 中纬 | 回归线 | 赤道 |
|---|---|---|---|---|---|
| 胞数 | 2 | 24 | 40 | 24 | 30 |
| 代号 | $1$ | $12^1$ | 20 | $12^2$ | 30 |

我们再加N或S代表南、北半球,赤道不用加。则12个10元环上十二面体所在的层数分布有四种,分别为:
- $-N1-N12^1-N12^2-S12^2-S12^1-S-S12^1-S12^2-N12^2-N12^1- (1\times 10)$
- $-N20-N12^1-N12^1-N20-30-S20-S12^1-S12^1-S20-30- (5\times 10)$
- $-N12^2-N20-N20-N12^2-30-S12^2-S20-S20-S12^2-30- (5\times 10)$
- $-30-30-30-30-30-30-30-30-30-30- (1\times 10)$
第一组那个环对应上图红色的十个十二面体,第四组那个环对应中间平躺的橙色十二面体环。第二组5个环与第一个环(红色)交链紧挨缠绕,第三组5个环与第四组的环(橙色)交链紧挨缠绕。
如果在Hopf纤维丛里画出这12个大圆,大圆所在平面对应的12个复数$k$的取值在球面$\mathbf S^2$上的分布恰为正二十面体12个顶点位置的分布!由此可见这12个环的地位其实是一样的。正120胞体的这些优美的性质正是我喜欢它的原因。
正交性
纤维丛还有很多漂亮的几何性质。六个坐标面可以分成绝对垂直的三对:$xy-zw、xz-wy、xw-yz$这样我们就有三种选$z_1$$z_2$所对应平面的方式:
$$ z_1=x+iy; z_2=z+iw $$$$ z_1=x+iz; z_2=y+iw $$$$ z_1=x+iw; z_2=y+iz $$
其实我们还能交换实部虚部:
$$ z_1=x+iy; z_2=w+iz $$$$ z_1=x+iz; z_2=w+iy $$$$ z_1=x+iw; z_2=z+iy $$
前三组其实描述的是左手Hopf纤维丛,后三组是右手纤维丛:我们交换两个坐标变量的位置相当于做了空间反射变换,所以$z_1=y+ix; z_2=w+iz$与$z_1=x+iy; z_2=z+iw$交换了两个变量,反射变换了两次又回到自身,它们是同为左手性的(其实Hopf纤维有中心对称性,它们表示的是同一个纤维丛)。
我们都选左手Hopf纤维,让我们同时画出这三个纤维丛:它们处处正交。
点击查看3D模型(需要支持webgl的浏览器,如Chrome)
它们在空间每一点正交: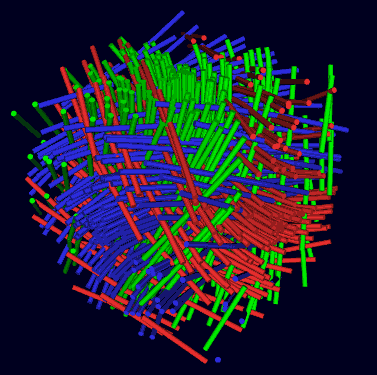
四维轮胎、环面外翻等拓补问题
为什么这些Hopf圆能组成一个像轮胎一样的圆环面?注意:你这里看到的圆环只是四维空间中的三维投影,所以我们要算出它原来的表达式:通过简单计算可以得到这个轮胎在四维空间坐标系方程是:$$\begin{cases}x^2+y^2=|z_1|^2 \\ z^2+w^2=|z_2|^2\end{cases}$$我们可以认为这是一个新的四维几何体的表面的一部分:$$\begin{cases}x^2+y^2\le |z_1|^2 \\ z^2+w^2\le |z_2|^2\end{cases}$$这个几何体是一个类似于圆柱的东西(注意当然不是圆柱柱)维基百科上把它叫做“doucylinder”,意思是“双圆柱”。我们将在下一节详细讨论它及和它相似的一类图形“直积形”(duoprism,直译过来是“双柱”),并将由此解释为什么圆环翻过来后经线和纬线居然能对调。
返回目录
环面外翻
我们研究四维空间却意外遇到了像锁链一样的两个圆、圆环的截面截出两个相交圆等三维空间中的几何知识。其实球极投影还展示了圆环面的另一个拓补性质:有孔的圆环是能够从里到外翻过来的。
什么是纤维丛?
直积
说到纤维丛,我们首先就得说什么是直积:设$A$、$B$是任意两个集合,在集合$A$中任意取一个元素$x$,在集合$B$中任意取一个元素$y$,组成一个有序对$(x,y)$,把这样的有序对作为新的元素,他们的全体组成的集合称为集合$A$和集合$B$的直积,记为$A×B$,即$A×B={(x,y)|x∈A且y∈B}$。
一些例子:
- 如果$x$是一条线段,$y$是一条线段,$x×y$就是一个长方形。
- 如果$x$是一个圆,$y$是一条线段,$x×y$就是圆柱。
- $R$本来是实数集,$R×R =〡(x,y)〡x∈R,y∈R〡$即为$xy$面上全体点的集合,$R×R$常常记作$R^2$。
如果$x$是一个圆,$y$也是一个圆呢?两个二维图形会直积出一个四维图形!它会是怎么样的呢?我们留作思考题,下节将着重介绍它
直积和纤维
直积和纤维有什么关系呢?我们可以这样理解直积,比如圆柱可以看作很多线段拼出来的或很多圆拼出来的:
你可以看到“纤维”的样子了。但由直积产生的纤维结构简单,没有多大意思,我们叫平凡纤维丛。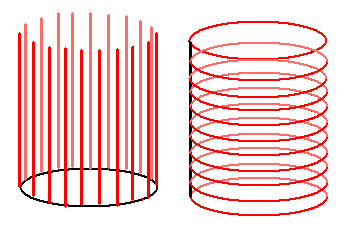
最简单的非平凡丛:莫比乌斯带
看看莫比乌斯带的划分——很像圆柱体上一根根竖着的母线——所以它的局部看起来是它的边和一条竖线的直积,但总体来看它多拧了一圈,所以和圆柱根本不一样,也不满足直积的定义:(x,y)|x∈A且y∈B}。
所以我们抽象定义纤维丛:每个纤维丛是一个连续满射$π: E → B$使得$E$对于某个$F$ (称为纤维)局部看来象直积空间$B × F$。
形象解释就是:有一堆毛茸茸的纤维,充满了一部分空间$E$(没有间隙),这些纤维的端点都在一张皮$B$上,被纤维充满的空间$E$中的任意一个点都对应到一根毛上,这跟毛的根部对应皮$B$上一个点,即满射$π: E → B$。四维空间中除了Hopf纤维丛还有Seifert纤维丛(维度预告片中有出现)等,以后我们将会看到。
Hopf纤维丛的E是超球$\mathbf S^3 $,B是球面$\mathbf S^2 $,F是圆$\mathbf S^1 $,当然圆没有端点,这只是形象的说明球面上的每一个点对应一个超球中的圆。拓扑学很热衷于找这种n-维球面$\mathbf S^n $之间的各种映射!比如他们发现在七维空间还存在这类似的纤维丛,可惜我们无法再清晰可视化出那个维度了。