四维空间(九):弯曲图形

内容简介
我们将在这篇文章重点讲一些四维空间中的曲面(胞)图形。我们先从一些新的角度(加厚、放样)来深刻了解一些重要的在之前文章更多几何体中粗略介绍过的旋转体图形(附有常见旋转体列表!),然后我将介绍一些新的几何体:双圆锥、Polytwister和四维螺旋形。
<!-- 多图预警 -->
回顾:平圆环面(Flat Torus 或 Clifford Torus)
双圆柱是两个圆形的直积形,它可以理解为底面是圆,侧面也是圆的广义柱体。什么,你说侧面是圆无法想象?那我告诉你:三维空间中的圆柱其实就是底面是线段,侧面是圆的几何体。
双圆柱是封闭的四维图形,它有两个全等的弯曲的侧面胞,每个侧胞都是实心圆与空心圆的直积。两个三维侧胞相交与一个二维曲面,它是两个空心圆形的直积形。下面重点来了:关键就是去理解这个四维空间中的二维曲面,双圆柱只不过是它的“实心化”。
根据直积的定义,那个二维曲面的方程是
$$
\begin{cases}x^2+y^2= r_1^2 \\ z^2+t^2= r_2^2\end{cases}
$$
我们看出那个二维曲面刚好可以放到过原点半径为$\sqrt{r_1^2+r_2^2}$的超球上,它的球极投影就是一个维度数学漫步最后一集的那个翻过去经纬度可以对调的圆环形!出于这个原因(其实还有拓扑学上的原因)我们把那个二维曲面叫做平圆环(flat torus)。下面我们就来着重理解这个平圆环。怎么理解?下面我们通过刚才对双圆柱的叙述方式再来叙述一下大家熟悉的圆柱:圆柱是圆形和线段的直积形,它可以理解为底面是圆,侧面是线段或底面是线段,侧面是圆的广义柱体。
圆柱是封闭的三维图形,它有一个弯曲的侧面,是线段与空心圆的直积。它还有“一个侧面”,是线段边界(两个端点)与实心圆的直积。由于线段边界两个端点是分离的,所以这“一个侧面”其实是两个圆,就是我们平时说的圆柱的两个底面。
我们看到,由于侧面多了一个维度,双圆柱把两个底面“联通”变成一个了,这归功于侧面是无头无尾闭合的圆形。但双圆柱作为一个好好的柱体,为什么投影下来却变成了有孔的环面?其实圆柱也一样!注意我们投影的不是双圆柱体本身,而是柱体“两侧胞”的交面。
同样,圆柱的一个弯曲侧面和另一个(其实是两个分开的圆的图形)侧面相交于底面和顶面的两个圆周——这才是我们要找的平圆环的降维类比。它是空心圆形和空心线段(就是两个端点)的直积形。这是一维曲线,方程是:
$$
\begin{cases}x^2+y^2= r_1^2 \\ z= \pm h/2\end{cases}
$$
我们看到它自然能放在球面上,而它的球极投影要么是大圆套小圆,要么是两个分开的小圆。
我们终于清楚了:有洞的圆环是一种把侧面投影下来压平再加投影放大变形了的产物。
我们得到了二维的圆环!我们成功把好端端的圆柱体投影成了有孔的二维圆环!它可以看成是二维空间中线段绕原点旋转产生的,或线段在圆上“放样”生成的图形——放样是指给定一条路径和一个横截面(不一定是二维),让横截面沿着路径移动扫过的图形,移动的过程中要保持横截面与移动方向垂直(三维空间中,这个条件限制了横截面维数必须小于三),所以这种移动是平移合旋转的组合。同样,有孔的圆环是圆在圆上“放样”生成的图形,它是平圆环压扁到三维空间的产物。当然,圆柱体也可以看成是线段在圆上“放样”生成的图形,只是线段摆放的角度不同,平圆环也是圆在圆上“放样”生成的图形,放样截面和路径是绝对垂直的两个圆,而有孔的圆环面则对应两个半垂直半平行的圆。我们看到,适当选择放样截面的角度可以节省一个维度。
构造圆环
再来说说三维圆环面:拓扑学上一个很经典的构造就是把一个正方形纸片的对边按相同方向粘起来,得到环面。分两步:第一部裹成圆筒,第二步把圆筒弯过来,把两端粘起来。但其实你从来没成功这样做出过圆环。你发现弯折没有弹性的圆柱纸筒时,内侧会受到挤压,所以做不出好看的圆环面。但如果允许在四维空间中弯曲这个圆筒就能够避免!我们将得到一个完美的平圆环:这也是平圆环“平”字的来源:平圆环上高斯曲率处处为零,纸张不会受到挤压或拉伸。这好比把长方形纸带两头粘到一起:在二维空间只能得到圆环,纸带肯定受到挤压或拉伸,三维空间形成圆柱侧面。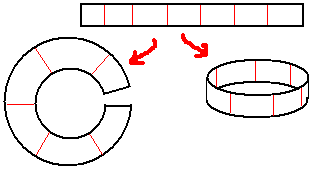
设想球与圆周的直积:球在三维空间中,圆周在二维空间中,直积的结果是一个五维空间中的三维曲体。球极投影得到球环或环球!球环可以认为是把球柱弯过来粘在一起得到的,那环球呢?它也可以!只不过具体做法有点不同。其实圆柱粘成圆环面就有两种方法:得到的两个圆环的经纬线刚好对调!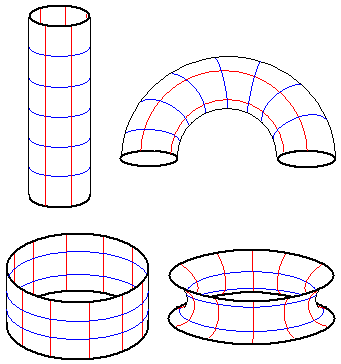
如果滚动五维空间的超球,你将看到球环慢慢外翻像经纬度对调一样变成了环球。其实球环、环球与球与圆周的直积拓补上是等价的。
最后我们挑战一下三个圆周的直积:圆周在二维空间中,直积的结果是一个六维空间中的三维曲体。用上面类似的放样法降维,可以得到五维空间的图形,再降维到四维空间中得到两种圆环环,它们都拓补等价于把圆环柱(以圆环为底胞的柱体)两头粘起来的物体,或把正方体各对面按相同方向粘在一起得到的东西。
加厚体
下面我们将从一个全新的角度来理解很多曲体。我们知道绳子是一维的,纸张是二维的,但严格来说这些都是错的,因为它们都有厚度。下面我们先来看看各种低维图形在三维空间拥有一定厚度过后变成什么样的了。首先是面:给平面厚度之后,面变成了一块有厚度的板子,同样曲面也能加厚(比如鸡蛋壳有微小的厚度):用一根垂直于曲面的直线去捅它,由于有厚度,相交不再是一个点而是一条线段,这个线段就是厚度;然后是曲线:用过每点垂直于曲线的直线去捅它;也都会探测到厚度,也就是曲线上的横截面都是圆,在垂直于曲线切线的两个方向上都要加厚度。
三维空间中的圆周加厚了就是圆环。
圆环又是圆的旋转体,这个圆的大小正好就反映了厚度,当它缩成一个点时,对应的圆环就退化成了没厚度的圆周。这说明了“旋转”与“加厚”操作可以互换顺序:一个在二维空间中加厚了的点变成圆,旋转产生的图形等于圆环;我们也可以说一个点旋转的轨迹是圆,把圆在三维空间加厚得到圆环。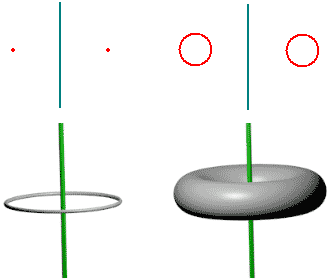
再看一个例子:把圆在二维空间加厚,等于旋转后的球面在三维空间加厚成有厚度的壳。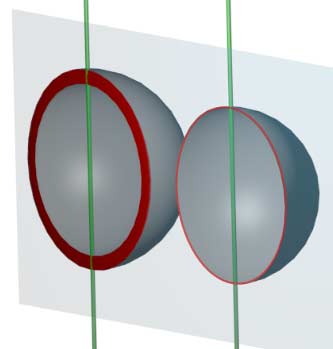
到了四维,一条直线加厚得到球柱,因为要补三个方向上的厚度,横截胞是球;一个圆周加厚得到球环;一张平面加厚得到平面与反映厚度大小的圆的直积(补两个方向),如果板子是长方形的就得到圆柱柱;一个球面加厚得到环球;最后三维胞加厚与三维空间中平面类似,只有一个方向加厚,得到一种“板子”。
“加厚”这个工具对于理解各种带圆环的图形的帮助是极大的。比如球环的定义是球绕外面的平面旋转得到的旋转体。设想让球的半径趋于零,则球环就近似于点绕外面的平面旋转,得到圆周;环球要稍微抽象一些,我们最初看到它的截面动画是突然出现一个空心球面,变厚再变薄并消失,如果截面动画只是突然出现了空心球面闪一下就消失了,这就是没厚度的球面了,换个视角,环球作为旋转体是圆环面绕包含它对称轴的平面旋转得到的,当圆环面小圆半径趋于零时圆环面就趋于一个圆周,圆周绕包含它对称轴的平面旋转就得到了球形。对于圆环的旋转体我们也可以采用这些方法理解它们: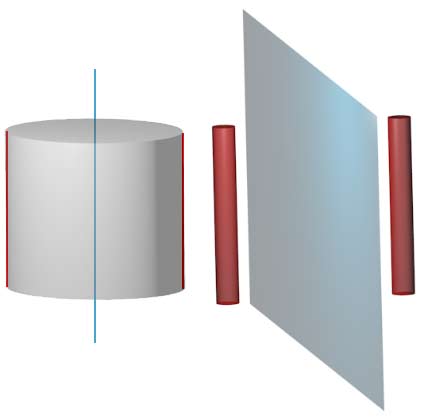
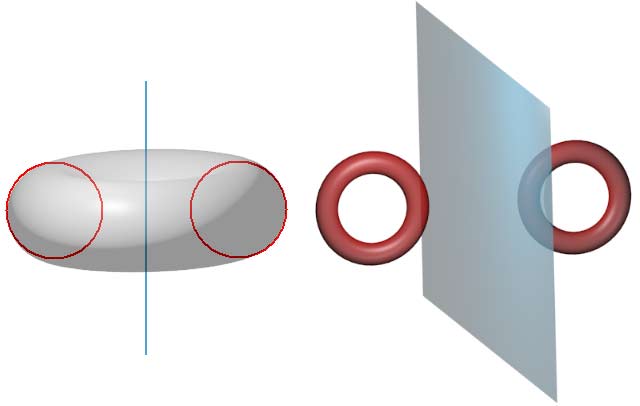
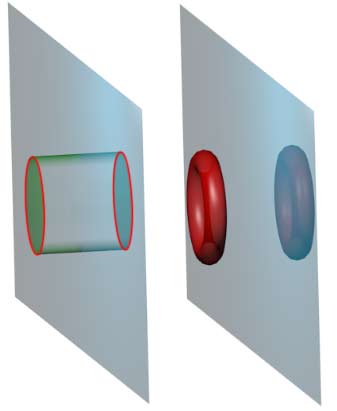
比如双圆环的这种加厚效应非常明显:斜着45°截双圆环会产生一种“老虎笼”(Tiger cage)的结构。

(双圆柱斜穿动画来自这个网站)明显看得出这些截面是双圆柱的截胞的棱边(平圆环)的加厚体(只是近似,截面不与法向垂直截不到均匀的厚度)。最后我想提醒的是说圆环是加厚体的时候,意思是把圆周在三维空间加厚成了实心的圆环;说把圆环加厚指的是把刚才的实心圆环的表面——圆环面加厚,得到双圆环。其实加厚圆环三维实体也可以,得到很薄的圆环柱,然而所有平直的三维图形加厚就是简单的柱化操作(高就是厚度),所以没什么讨论的意义。
加厚与放样体高维推广
对于四维空间,我们分析得到一条直线加厚得到球柱,一条曲线加厚得到的东西其实就是放样体:球沿曲线的放样。
一张平面加厚得到圆柱柱,对于曲面来说是什么呢?曲面上每点都有法平面,加厚时法平面上所有的方向都获得了均匀的厚度,所以法平面截加厚体得到圆。我们可以认为加厚体是圆周沿着二维的曲面放样出来的:圆周沿着二维的曲面移动,同时保持圆周垂直于曲面的切平面。这个方向是唯一的。如果截面不是圆(对应非均匀加厚),放样中截面就可以自转。三维空间也存在这种现象,比如一些扭棱体。四维空间中非圆形截面放样体就更抽象了,我暂时想到了下面这两个图形:
- 两个二维圆环的直积:矩形在平圆环上放样;
- 以有厚度的球壳为底胞的柱体(球柱侧面加厚体):矩形在球面上放样;
- 以有厚度的圆环壳为底胞的柱体(圆环柱侧面加厚体):矩形在环面上放样;
最后我想再总结一下直积与放样的关系:直积是一种特殊的放样:路径图形和截面图形所在空间绝对垂直,所以截面图形只需做平移;一般都放样是路径图形只和截面图形某一点的切空间垂直,平移到其他位置就要加上旋转来修正。如果没有维度限制,我们总是可以通过旋转截面到与路径绝对垂直的位置,就把所有放样变成了直积,所以放样和直积拓补上完全等价(同胚)。
双锥体
我们知道圆柱体的类比有球柱、圆柱柱、双圆柱,圆锥的类比有球锥、圆柱锥、圆锥锥。下面我们将看到还存在类似于双圆柱那样的双圆锥!!我将给出三种理解它的方法。
作为旋转体
以圆锥底面为旋转平面做旋转,就会得到一个高度对称的图形——双圆锥。首先,圆锥底面圆周在旋转平面上不动,而锥体顶点旋转一周得到与圆锥底面绝对垂直的圆周,这两个圆的地位其实是一样的(可能不太直观)。注意这两个圆是中空结构,是双圆锥表面上突出的棱,双圆锥上并没有二维的实心圆面。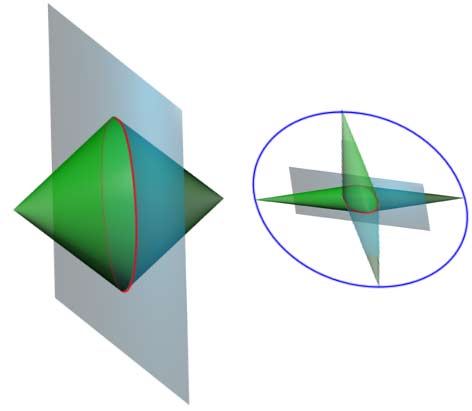
作为双锥形
真正要理解两个圆地位是相等的要先理解一种新的几何体——双锥形。它的定义是:给定两个中心都在原点的绝对垂直的平面图形$A$和$B$,取它们的凸包,记作$A+B$(Schläfli符号)。什么是凸包?形象地说就是把图形外面蒙上一层保鲜膜,紧紧地裹起来。比如正方形就是两条相互垂直线段的凸包,正八面体是三条相互垂直线段的凸包,或正方形与垂直线段的凸包。两个n-棱锥倒扣起来形成的双锥就是正多边形和线段的凸包,我们注意到它的对偶多面体就是n-棱柱。
接下来到四维,正十六胞体就是四条相互垂直线段的凸包,或两个绝对垂直的正方形的凸包,或正八面体和垂直线段的凸包……更一般地,正p、q边形的凸包我们就叫p,q-双锥形(p,q-duopyramid),它的对偶多胞体是p,q-直积形(p,q-duoprism)。
把这些东西膨胀到超球上投影下来就是南北极各有p、q个点的两个圆周和中间南北走向的棱线。两个多边形上的点两两连接,每个胞都是由各自多边形上的边两两组合形成的四面体胞。
双圆柱和双圆锥也继承了直积形与双锥形间的对偶关系。双圆柱有两个全等的侧胞,双圆锥有两个全等的圆形棱。双圆柱唯一的的二维棱平圆环对应双圆锥唯一的曲胞。
我们知道三维空间中圆锥体也是可以滚动的,但不是直着滚而是绕着顶点打转。我们将在后面看到双圆锥的滚动方式非常特殊,因为$xy$平面、$zw$平面上的两圆同时充当了顶点的角色。由于滚动的分析很麻烦这里就不展开了。
(更新:基于4D刚体力学的滚动模拟器做好了,戳这里!)
截面动画
重要旋转体列表
下面我们来总结一下各种各样常见的四维旋转体:此表给出了它们是怎样的三维图形、绕什么平面旋转得到。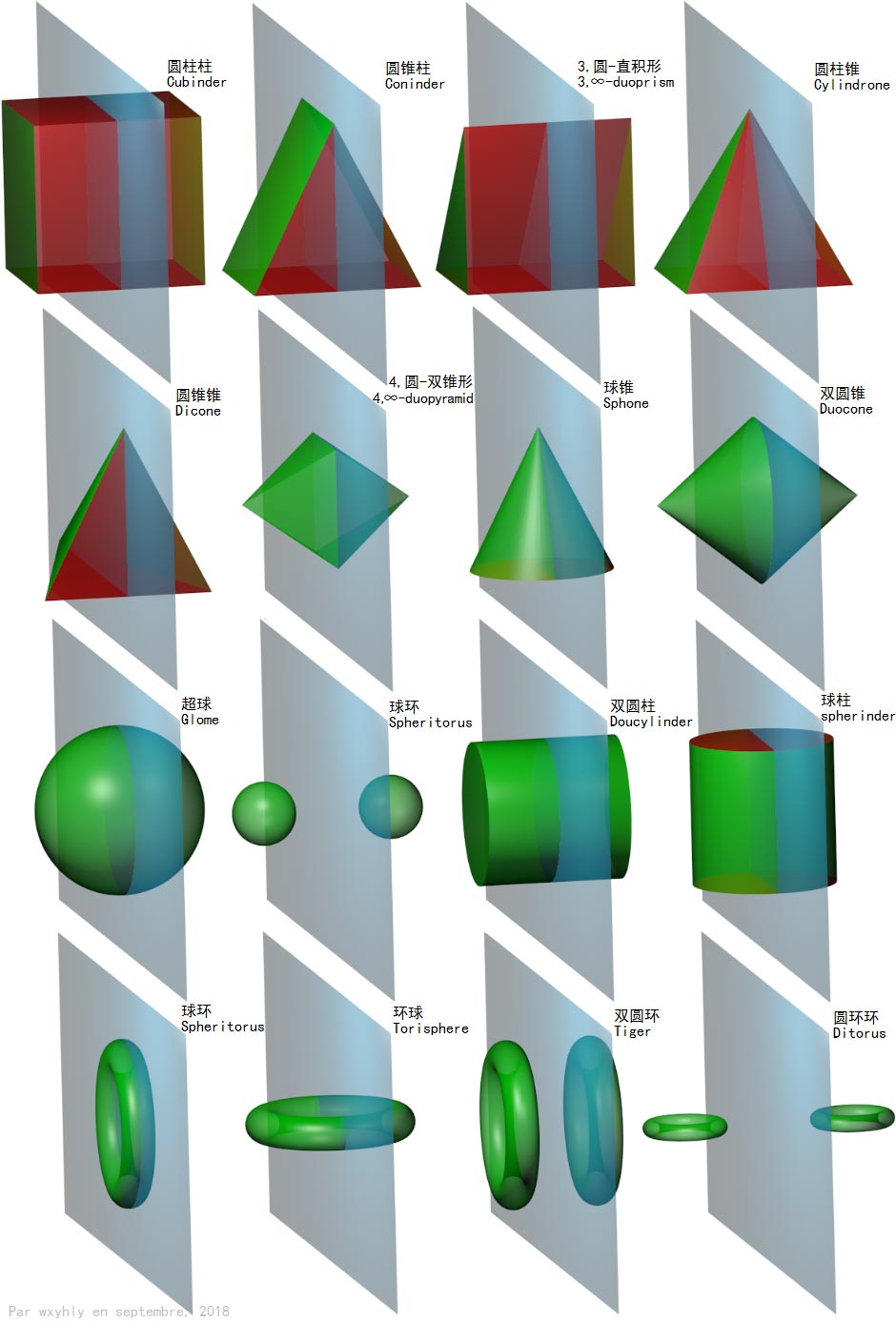
我把旋转后生成四维曲胞的三维图形表面部分涂绿了,涂成红色的部分旋转后得到平直的三维胞。
Polytwister
我们又多了一样创造几何体的工具——凸包,其实菱形十二面体就是正方体和正八面体的凸包;双圆柱就是平圆环的凸包。双圆柱是两个正交的圆的凸包,如果圆之间是斜着的会怎样?大概会得到一种类似斜双锥一样的东西,没什么意思。但是我们知道,Hopf纤维丛上的圆周之间都夹等角,每个圆周$z_2=k z_1$都可以通过复数$k$对应到一个抽象的球面上。如果我们把正多面体框架膨胀到这个球面上,那么这些框架上的点对应的Hopf圆周之间将保持一种有原来正多面体对称性的高度对称的结构,我们再取所有这些圆的凸包将会得到一种叫Polytwister(多扭体?)的东西。我是从这个网站了解到Polytwister的。 (25年更新:后面我发现有两种Polytwister的定义,一种是上面说的凸包,得到的棱角偏软,另一种是取很多双圆柱的交集,得到的棱角偏硬,下面展示的其实都是硬polytwister。)
Hopf圆周之间在球极投影下是扣在一起的,所以我们取凸包的时候就得到一些被扭曲了一圈的带子,比如下面是正十二面体对应的Polytwister。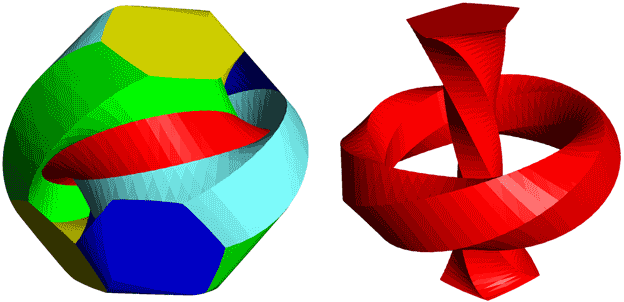
剪开这些扭曲了一圈的带子我们得到Polytwister的展开图:
值得一提的是,取凸包的时候那些中空的五边形在边缘那些骨架上被撑平了,把Polytwister放到地上相切的部分就是这些五边形。它的侧面有点类似于双圆柱,可以沿一个方向滚动,而另一些方向有棱角。它的局部很像五边形与圆的直积,但整体却扭曲了一圈!至于往前滚动的时候这个东西会不会发生扭曲方向的自转我就不知道了。
以上两副图都来自刚才提到的这个网站,上面还有其他正多面体、半正多面体,甚至星形正多面体对应的Polytwister的图像!这一切都得感谢Hopf纤维化的“鬼斧神工”。Polytwister可以看作部分离散化的Hopf纤维丛,完全离散化的例子有正六百胞体,它是正二十面体对应的Polytwister进一步离散化(把十二个Hopf圆换成十边形后取凸包,得到正六百胞体的120个顶点)的结果:
四维螺旋面
三维的螺旋形是点在做圆周运动,然后同时往垂直方向平移产生的轨迹。到了四维,我们不妨类比为一个圆周一边自转一边往垂直的方向平移扫过的二维曲面,那么它沿平移方向上的截面动画就是旋转的圆。注意它扫过的区域是是一个球面,里面可以放进一个实心球,随时间平移就成了球柱,也就是说这个“弹簧”可以套在球柱上面。
下面是各种方向上的截面动画:
它的平行投影自相交很严重,看起来像是螺旋面:
还有没有其他可能的形状?比如正方形一边自转一边平移?(注意,这里的自转限制在了与平移方向垂直的三维空间中,而且要得到四维图形,正方形不能在它自己所在平面内转动)这种“方弹簧”可以套在圆柱柱上面!其实还有更疯狂的构造:螺旋线一边自转一边平移会得到什么?螺旋线可以绕两种不同的方向自转,这些东西我已经无法想象了,但不妨碍我们画一画它的截面动画:第一种是绕垂直于螺旋平移方向旋转,不得不说太奇怪了。
另一种是绕螺旋平移方向旋转,但由于螺线的特性可以认为没发生旋转,转而等价于螺旋线上下平移,最后得到一种斜着的螺旋线柱面。
最后或许你还会问,为什么螺旋线的类比就要是2维曲面,为什么不继续是一维的四维空间曲线?确实有可能,但我目前还没找到比较像螺旋的线状东西。。。

