趣题:五维立方体截面
本文分两部分,第一部分是关于五维立方体截面谜题,第二部分是对一类四维多胞体性质的探讨。我们要解决五维空间中的问题,但主要还是以四维空间中的讨论为主。
part 1
先来一道只涉及四维(不涉及五维)的题热热身吧
我们知道,正方体可以被斜着截出正六边形截面,它与正方体所有面都相交;推广到四维,我们希望超立方体也可以被“斜着”截出一种截胞(胞指三维的“面”,下同),它与超立方体所有八个面(立方体胞)都相交,当然符合要求的“斜着”截的方法很多,我们要一种最“对称”的截法,即选垂直于体(最长)对角线的过超立方体体心的截面,这样能满足于所有面都相交的要求吗?会截出什么图形?如果截面不过超立方体体心,我们又可能得到哪些形状的截面?
答案是能截得正八面体!(它的棱长为$\sqrt 2$,经过所有正方形的面对角线)截面不过体心我们还能得到正四面体、截角四面体等形状。
看来选垂直于体对角线的过超立方体体心的截面,既满足与所有面相交的要求还满足最对称,如果我们继续,推广到五维空间,即选垂直于五维立方体的体对角线且过五维立方体体心的截面(四维超平面)截五维立方体,我们应该会得到一个四维图形X,我们认为这个四维图形X是线段(斜截正方形得)->正六边形->正八面体->X这样类比来的。你能说出X的基本特征参数并大致画出它的球极投影吗?
寻找图形X
四维图形X应该是通过截五维立方体得到的一个四维的截面图形,它与五维立方体10个面(即10个超立方体“面”,想想为什么它有10个面)相交得到,既然有对称性,那可不可能是正十胞体?很遗憾的是,正10胞体不存在,因为四维空间中正多胞体只有正五、八、十六、二十四、一百二十、六百胞体这六种,我们没听说过什么“正10胞体”。其实我们选择垂直体对角线且过体心的截面的原因就是这个截面与五维立方体的所有四维面的“地位”(比如夹角,但我们还没讨论过五维空间中的夹角)是一样的,所以我们有理由相信截得的四维图形X的十个面是全等的。每个面是什么形状的呢?感觉没有线索。
当我们研究高维空间的问题没思路太抽象时一般有两种解决方法:一是用代数法(比如解决四维空间两平面夹角问题),二是想想低维空间的情形。我们先尽量不用代数法,那样显得有点无趣。所以我们转而想想四维情形:想想四维立方体的各个垂直于体对角线的不一定过体心的一系列截面(三维面),这一系列三维图形有一个特点,就是组成它们的二维面都是三角形或六边形。这些三角形或六边形正是三维情形中正方体垂直体对角线截得的一系列截面!它的道理很简单,当我们截n维空间的一图形时,它的n-1维边界是n维空间的子空间,也相应被截了,在正方体的一系列类比中,截面交n-1维子空间得到“子截面”也垂直于n-1维立方体的体对角线。总结下来关于X我们有这些信息:
- X由10个全等的胞构成;
- 胞的形状应该是四面体、截角四面体或八面体之中的一种。
这里值得注意的是,过n维立方体体心的截面截到n维立方体的n-1维面(n-1维立方体)并不会过n-1维立方体体心,因为n-1维面离n维立方体的体心有边长一半的距离,所以我们排除胞的形状是八面体。
由于五维立方体每个四维面都有平行的对面,所以截面X的每个三维面也有平行的对面,这让我们想到了还可以像描述正120胞体一样“分层”描述这个图形X:
| 位置 | 胞数 |
|---|---|
| 北极 | 1 |
| 北半球 | 4 |
| 南半球 | 4 |
| 南极 | 1 |
注意为什么我能肯定的给出北半球、南半球是4,因为X的胞的形状只能是四面体或截角四面体,所以与北极相邻的胞必为4,截角四面体有4个胞与北极共六边形,另四个与之共三角形,显然距离不一样,所以北极点外“第一圈”的胞数还是4。
其实X的胞不可能是四面体。如果是四面体,北极点外“第一圈”四面体朝外的四个顶点两两间会有沟壑,填充这些沟壑至少得用6个四面体,与上面的分层描述不符,当然还有种情况是“第一圈”四面体朝外的四个顶点是共用的,这就是正五胞体,当然对称性不允许其他情况,比如只共用2个或三个顶点,所以我们排除了X的胞是四面体的所有可能。
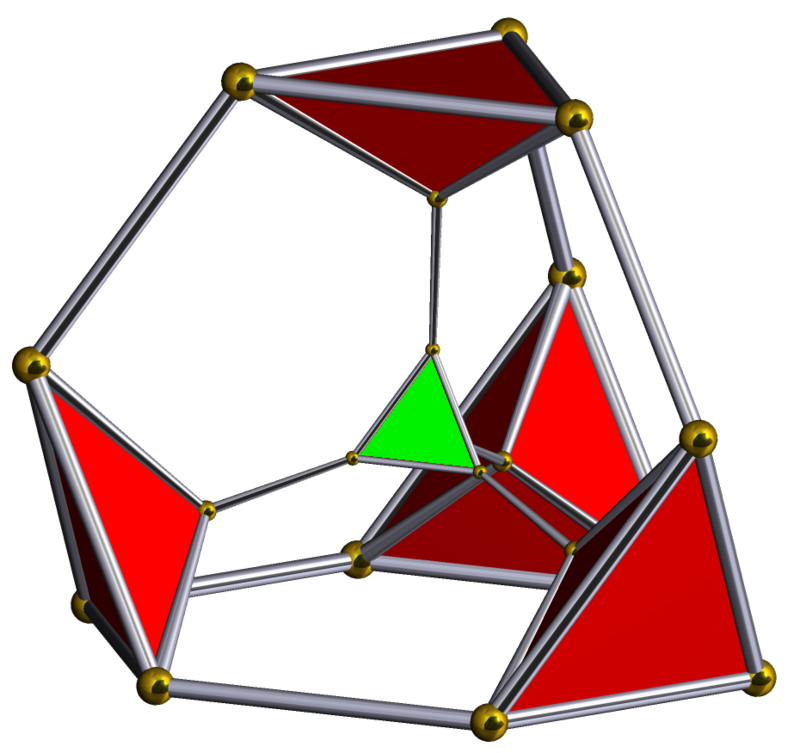
所以最后一种就是答案了:截角四面体。北极点外“第一圈”截角四面体与极点共六边形,与南极共三角形;南极点外“第一圈”截角四面体与南极点共六边形,与北极共三角形。几何体X就是过截角五胞体(bitruncated 5-cell),具体可参见英文维基对应条目,这个多胞体在jenn3d软件上也找得到。
part 2
jenn3d软件上给出了过截角多胞体家族,那到底什么是过截角呢?过截角就是截角时截过头了,但三维空间中过截角多面体正好就是原多面体对偶多面体的截角多面体。
比如截正方体,首先得到图中第三个(均匀)截角正方体,再得到第五个截半正方体,这是能截得的最大临界状态,超过后就是过截角了(第七个),但从八面体出发,首先得到图中第七个(均匀)截角正方体,再得到第五个截半正方体(也可以叫截半八面体,它的英语名称叫Cuboctahedron,直译“立方八面体”),然后就是过截角八面体(第三个)。
我们看到三维空间没必要用过截角,但四维空间中就不一样了。我们不妨看一看正五胞体截角的全过程。
首先我们得到截角正五胞体,截到中点时得到截半正五胞体。超过中点后会得到什么图形?
(以下图片均来自英文维基百科)

截半正五胞体有正八面体胞核正四面体胞,正八面体是“截半正四面体”,继续截会让正八面体变回截角正四面体,正四面体也会变成截角正四面体,所以所有胞都变成了截角正四面体,这就是过截角正五胞体。

不是所有过截角正多胞体都只有一种胞围成,只有正多胞体是自对偶时才有这种情况,还有一种很漂亮的过截角正多胞体是过截角正二十四胞体。(正二十四胞体自对偶)
现在我们能讨论垂直于五维立方体的体对角线的面(四维面)在任意位置的截面的图形了。我们可以想象截面移动形成截面动画:先看到正五胞体从一个点开始变大,然后被截角,即截角正五胞体,继续截角得到截半正五胞体、过截角正五胞体,然后又变成截半正五胞体、截角正五胞体、最后恢复为正五胞体,变小消失。