#本文讨论的是纯空间上的几何，而不是物理上的时空！推荐视频《维度：数学漫步》对四维空间作初步了解
研究四维空间中的正多胞体的基本方法还是类比：所以你恐怕得先对我们三维中的正多面体有点了解（可参看Matrix67对正多面体的介绍）。
正多胞体一共有六个：单形（正五胞体）、超立方体（正八胞体）、正十六胞体、正二十四胞体、正一百二十胞体、正六百胞体。影片中只展现了它们的投影图（平行投影和球极投影）和一些基本几何信息，我们今天来看看它们具体是怎样构成的。其中除了正二十四胞体以外其他五种正多胞体我们都能找到三维类比——它们分别是正四面体、正方体、正八面体、正十二面体和正二十面体。
网站 www.software3d.com 上的120号模型 by Robert Webb
特色内容
- 16号、24号的类比过程
- 超球最密堆积问题
- 120号的分层结构
- 镶嵌
本文目录：
单形（正五胞体）
《维度》第三集中讲的第一个四维几何体就是单形（Simplex）。虽然影片中的类比很合理，但我们要知道为上么这样类比是对的——随便画五个点连起来就是单形？为了好理解，我们从0维开始：
- 0维——一个点（0-单形）；
- 1维：这个点和它外面一点连线，得到一条线段（1-单形）；
- 2维：这条线段和它外面一点连线，得到一个三角形，其中这个三角形底边为原线段，另外两条边分别由外面一点与原线段端点连线所得（2-单形）；
- 3维：这个三角形和它外面一点连线，得到一个四面体，其中这个四面体底面为原三角形，另外三个面分别由外面一点与原三角形三边组成三角形所得（3-单形）；
- 4维：这个四面体和它外面一点连线，得到一个五胞体，其中这个五胞体底胞为原四面体，另外四个胞分别由外面一点与原四面体四面组成四面体所得（4-单形）；
- 5维：这个五胞体和它外面一点连线，得到一个“六超胞体”……
- ……
我们看到，一个图形与它外面一点的连线正是构成锥体的方式。而n维空间的单形就是一系列这样的锥体，我们可以把三角形看成“线段锥”、四面体看成三棱锥、五胞体看成“四面体锥”……
超立方体（正八胞体）
对超立方体网上的解释太多了，且它是最容易理解的，我就没必要再讲了。
正十六胞体
奇怪的是《维度》视频里讲完超立方体就把正十六胞体跳过直接讲正二十四胞体了，其实正十六胞体也很精彩。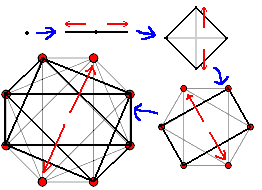
得到的这一系列n维几何体叫n-cross。正十六胞体是三维空间中正八面体的类比，所以我们要先清楚了解正八面体。正八面体是正方体的对偶多面体——在几何学中，若一种多面体的每个顶点均能对应到另一种多面体上的每个面的中心，它就是对方的对偶多面体。
正八面体给我们还有一个更直观的感受，那就是它像两个倒扣着的金字塔（四棱锥）。两个金字塔的底面形成了一个中空的正方形结构。其实我们在正十六胞体里也能找到中空的八面体结构！它可以看作两个倒扣着的“八面体锥”，左下图是正八面体顶点过极点的球极投影，可以清楚看到中间八面体框架。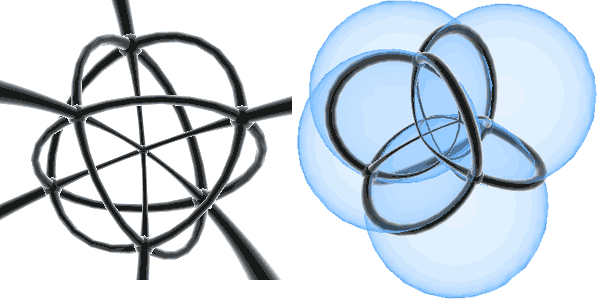
正十六胞体球极投影还能看成四个球体两两相交（右图），所以它可以用来画4个集合的韦恩图。
返回目录
正二十四胞体
这是《维度》影片中讲述者最喜爱的图形，影片中说它没有三维类比其实是不对的。它有一个三维类比——菱形十二面体。和搞清正十六胞体的步骤一样，我们要先清楚了解菱形十二面体。
可能之前很多人都没听说过菱形十二面体，现在我们从大家最熟悉的正方体开始来讲一讲它的形成过程。
- 正方体有8个顶点，六个面。我们设想抓住这6个面的面心处往外拉，把每个面都拉得像四棱锥：
- 这样继续往外扩展，直到相邻两个三角形面共面，它们构成一个菱形。
我们现在观察一下：新得到的菱形十二面体一共有两类顶点：原来正方体8个顶点（每点发出3条棱）+面心“拉出”的6个顶点（每点发出4条棱），菱形十二面体的每个菱形面都是相邻两个三角形面共面形成，所以一个菱形面对应原正方体的一条棱，正方体刚好12条棱，所以我们也有12个菱形。而原来的正方形的棱都已经不复存在——它们已经变成菱形里面的对角线了，不再是图形的边界。
下面该到四维里了：
- 超立方体有16个顶点，八个胞。我们设想抓住这八个立方体胞的体心处往外拉，把每个胞都拉得像立方体锥：
- 这样继续往外扩展，直到相邻两个四棱锥共胞，它们构成一个八面体（两个倒扣着的四棱锥组成一个）。
我们现在观察一下：新得到的多胞体一共有两类顶点：原来超立方体16个顶点（每点发出4条棱）+胞心“拉出”的8个顶点（每点发出4条棱），这个多胞体的每个八面体都是相邻两个四棱锥共胞形成，所以一个八面体胞对应原超立方体的一个二维正方形面，超立方体刚好24个二维面，所以我们也有24个八面体。而原来的超立方体的二维面都已经不复存在——它们已经变成八面体胞里面的中空的正方形结构，不再是图形的边界，但正方形的边界还是多胞体的边界，所以这导致看它的投影图里含有一个超立方体——其实只是一个中空的结构（想想棱形十二面体吧）。
我们看到多胞体的两类顶点：原来超立方体16个顶点和胞心“拉出”的8个顶点都是每点发出4条棱，且可以几何证明那个八面体是正八面体！所以这个菱形十二面体的高维类比居然华丽升级成了正多胞体，不可思议！我是这样理解这个“逆袭”现象的：超立方体的体对角线是一个整数2，这使得对角方向的几何图形的边和原坐标轴方向上的边才有可能等长，进而才有所有棱长相等的可能吧。
返回目录
最密堆积问题
有类很著名的几何问题就是同样大小的圆或球的最密堆积问题，二维情形是这样的：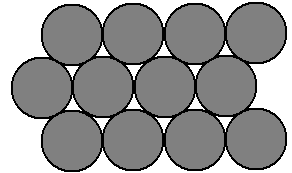
三维一般有两种最密堆积：面心堆积和六方堆积，它们区别是上下两层一个是一样的，一个转了180°。
其中第一幅图面心堆积的外框是一个截半立方体——立方体截去两角，直到相邻顶点截出的三角面刚好交于一点。它是菱形十二面体的对偶多面体，其中截出的三角面对应菱形十二面体的8个正方形顶点，剩下被截成45°正方形的面对应菱形十二面体面心拉出的6个顶点。我们来看三维最密堆积的结构：我们把它解析为三层的叠加：其中中间（白色）那层球就是平面中的球最密堆积方法，上、下面三个球刚好隔一个放进中间球堆积形成的六个凹陷里面。
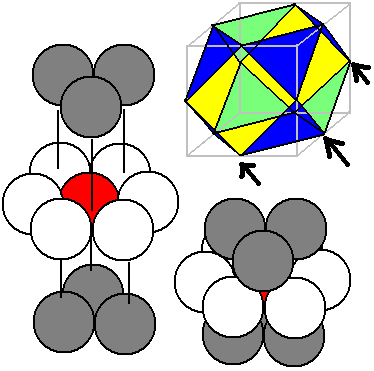
四维的超球最密堆积应该也分三层：中间这层就是三维的最密堆积。问题是“上”、“下”两层的超球该填在哪？我们也可以在上层试着隔一个填入一个球的间隙里：这里可以填六个正方形对进去的三棱柱或六个三角形对进去的四面体，但这个四面体感觉体积太小了，似乎填不进（不是填不进，而是超球占下层空间小的话空间利用率会变低，进而不是最密堆积）所以我们选择填入正方形对进去的三棱柱里；下层还需不需要交错着填呢？不需要，因为交错着填要求我们要把下层的球填到狭窄的四面体中去，这不是我们想做的，再说没有规定上下层必须交错（三维空间另一种最密堆积六方堆积上下层就是一样的）所以我们上下层一共12个超球的投影下来的位置是重合的，即下图中6个蓝色点。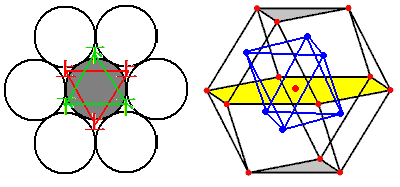
结果：上层有六个超球，构成正八面体，下层也一样，最密堆积中一个超球紧密相邻的球一共6+12+6=24个！一个熟悉的数字！事实，我们剖分正24胞体的球极投影就能发现最中间那层截半立方体！截半立方体里面的正八面体当然就是下层那六个点构成的，上层的就是最外面最大的已截掉的八面体的6个顶点。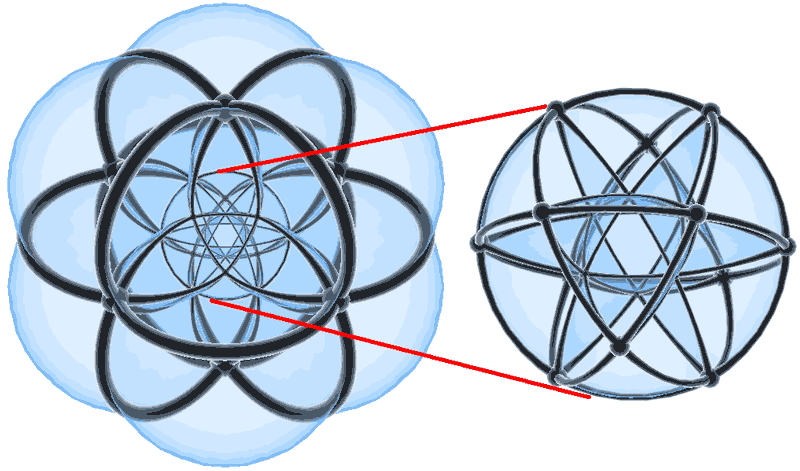
我们通过这个思路又给了正二十四胞体另一个类比解释：它是三维空间截半立方体的四维推广：其实这和菱形十二面体推广不矛盾，因为菱形十二面体与截半立方体对偶，而正二十四胞体是自对偶——它顶点和胞数都是24！我们也给出了正二十四胞体在超球上的一种胞的分布情况：
| 位置 | 胞数 | 说明 |
|---|---|---|
| 北极 | 1 | 最外面的八面体 |
| 北半球 | 8 | 与北极八面体8个面相邻 |
| 赤道 | 6 | 与南\北极八面体6个顶点相对 |
| 南半球 | 8 | 与南极八面体8个面相邻 |
| 南极 | 1 | 最里面的八面体 |
我们再换个角度思考：正二十四胞体是不是像截半立方体那样是什么图形截角得到的呢？由于正二十四胞体每个胞是正八面体，如果它是截角得到的截胞，则截下的顶点应该发出8条棱，显然不是超立方体或正十六胞体了，所以这个类比是失败的。
MathWorld网站上说，五维空间中的最密堆积也是这样类比的，但6、7维空间中的最密堆积的基本结构是cross——八面体、正16胞体对应的那一系列类比出的几何体。八维空间中的最密堆积又是两个面心立方堆积的组合，而其他一些高维空间中的最密堆积还有乱的（既超球排列没有周期规律）。
返回目录
正一百二十胞体
《维度》影片中讲述者最喜爱的图形是24号，而我最喜欢的图形就是120号。我曾经用掉一个本子满篇画正一百二十胞体球极投影结构。
它的球极投影图就是119个有着十二个面的“泡泡”组成的一个大泡泡。有人把119个十二面体3d打印了出来，感觉就是一套目的是拼出一个大十二面体的拼图玩具。我们现在要搞清的是这里面119个“泡泡”是怎么做到无缝精致拼接在一起的。注意，我们现在不再从五边形-正十二面体-正一百二十胞体这样一层一层类比了。正十二面体结构太复杂了，所以我们直接把它当作超球上的一种正十二面体密铺的图案。既然这样我们先一层一层看十二面体在超球上的分布情况：
| 位置 | 胞数 | 说明 |
|---|---|---|
| 北极 | 1 | 最外面的12面体 |
| 北极圈 | 12 | 与北极12面体12个面相邻 |
| 中纬度 | 20 | 填补北极圈对应北极12面体20个顶点位置的凹陷 |
| 北回归线 | 12 | 分别与北极圈12个12面体靠南的12个面相邻 |
| 赤道 | 30 | 填补对应南北极12面体30条棱上的30个空隙 |
| 南回归线 | 12 | 分别与北回归线12个12面体靠南的12个面相邻 |
| 中纬度 | 20 | 填补南极圈对应南极12面体20个顶点位置的凹陷 |
| 南极圈 | 12 | 分别与南回归线12个12面体靠南的12个面相邻，且与南极12面体12个面相邻 |
| 南极 | 1 | 最里面的12面体 |
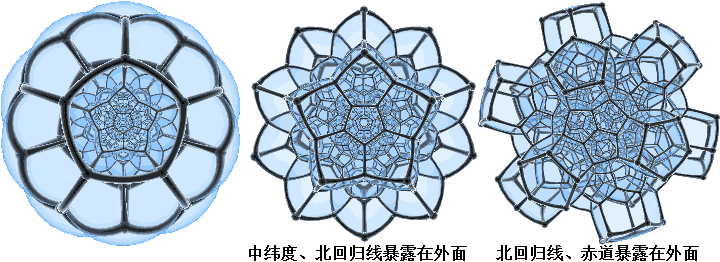
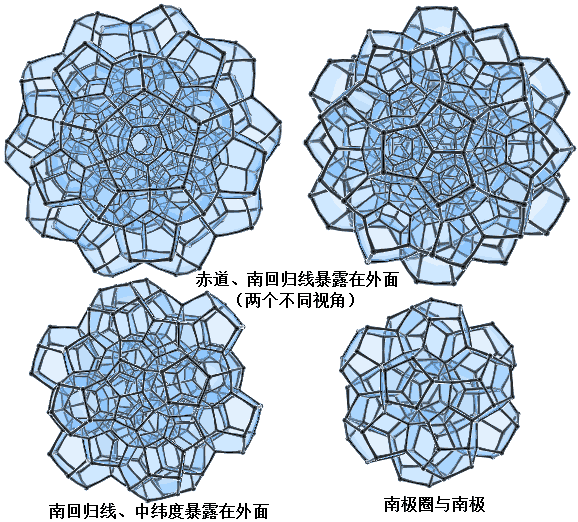
可能还有疑惑的就是中间那圈30个12面体了，它们分布在12面体棱上的30个位置。我们把正十二面体所有棱的中点连起来得到了一个“截半二十面体”，画出来长这样：（以下图片均出自en.wikipedia Icosidodecahedron页面）
其中你能发现很多正十边形的中空结构。它的球极投影能更好反映这些正十边形：
好神奇！球极投影图就是六个圆周。我很喜欢徒手画一些多面体的球极投影图，我遇到其他投影图是圆周的还有正八面体：3个圆、截半立方体：4个圆（好熟悉，对，它就是讲最密堆积是出现的图形）。其实只要一个顶点发出4条棱的（半）正多面体都能投出圆形。说明我们在30个正十二面体中能发现六个首尾相接的环形结构，其中每个环上都有10个正十二面体，因此**每两个正十二面体形成的二胞角等于$180°-360°/10=144°$**。其实整个正一百二十胞体能分成12个大环，每个环上10个正十二面体都是首尾相接的。我们将在下一节纤维丛中具体描述这些环形结构。
返回目录
正六百胞体
正六百胞体与正120胞体对偶，正120胞体是十二面体胞中心的地方正六百胞体就有一个发出12条棱的顶点，正六百胞体是四面体体胞中心的地方正120胞体就有一个发出4条棱的顶点，所以根据对偶性（顶点-胞、棱-边）正六百胞体没有什么新的结构了，我们就暂不讨论了。至于有人说正六百胞体球极投影里面有单形（正五胞体）展开图，我认为这只是巧合看起来像而已，它们无实际联系。
镶嵌
还记得《维度》影片中出现的那些蜥蜴吗？我们仔细看那幅画有蜥蜴的画：二维的蜥蜴可以无缝地铺满整个二维空间。这幅画的原作是埃舍尔（Escher，有一本介绍他的很好的书《哥德尔艾舍尔巴赫：集异璧之大成》），他是一个奇特的画家，专门画错觉图形和数学几何图形。
这种图形密铺我们叫做“欧几里得镶嵌”。当然我们最关心的还是正多边形镶嵌:
- 二维只有三角形、正方形、正六边形镶嵌。
- 三维空间只有正方体镶嵌。但放宽点不限于正多面体镶嵌，比如我们发现菱形十二面体能够密铺三维空间！
- 四维空间有三种正多胞体镶嵌：超立方体、正十六胞体、正二十四胞体。但除了超立方体其他两个我还没去想象它们怎么堆叠的……大家有兴趣可以思考一下。
为什么要叫“欧几里得镶嵌”？难到还有“非欧几里得镶嵌”吗？“欧几里得”指平直空间，它的曲率为0。前面我们说我们把正一百二十胞体看成超球表面上的“图案”，这就是球面镶嵌，球面具有大于0的曲率。正多面体也可以看做二维的球面镶嵌，这才是正多面体、正多胞体的本质。还有一种“双曲镶嵌”，它的曲率小于0。双曲镶嵌也是相当震撼的，是埃舍尔很多代表画作的题材。