#本文讨论的是纯空间上的欧氏四维几何，而不是物理上的闵氏四维时空！（试想如果有二维生物，他们可能会认为三维是2维空间+时间，这就是三维时空，而不是我们的三维欧氏几何空间）本文不讨论把第4个方向当时间的情况！所以本文不会涉及物理相对论等内容。
图片来自en.wikipedia：By Vitaly Ostrosablin
#本文针对于对四维空间有初步了解（比如知道超立方体等）的读者写的。如还没了解，推荐视频《维度：数学漫步》（它对我数学影响深远），CFY的这篇文章对四维空间有更基础的介绍。（CFY和我一起研究的四维空间，可能有些介绍有重复）
四维空间太抽象，所以我们不能直接感性地接触它（直接看到或摸到），但我们可以用类比法或解析法像“盲人摸象”那样建立起对它的认识。类比法较直观，但对想象力要求高，且不严谨；解析法（计算法）严谨，但缺乏直观几何意义，滥用会把几何沦为代数，只有两者结合起来才能更好地认识四维空间。
特色内容
- 各种柱体、锥体
- 超体积、表体积的计算
本文目录：
超立方体、超长方体类比性质
关于面的形状、面数、顶点数等基本参数我就不罗嗦了，我们看其它性质：
- 和正方体一样，它是柱体，它的“底胞”是正方体（即“3维的底面”，我们以后说胞指3维面），它的高$h$就是棱长，等于底胞正方体的边长。
- 它是特殊的“超长方体”，“超长方体”是特殊的“平行8胞体”。（类比：正方体、长方体、平行6面体）
- 棱长为$a$cm的超立方体“超体积”为$a^4$cm4，它有着“表体积”$8a^3$cm3。（类比：正方体体积和表面积）
- 根据勾股定理或坐标计算，单位超立方体体对角线（即超立方体上最远两点距离）为一整数：$\sqrt4=2$，（而正方体$\sqrt3$、正方形$\sqrt2$是无理数）
- 超长方体很多性质和长方体类似，它的尺寸要四个参数描述：长$a$、宽$b$、高$c$、厚$d$，超体积$=abcd$，表体积$=2(bcd+acd+abd+abc)$……
一般柱体
一般柱体是以任意三维几何体为底面，沿不在底面所在三维空间的方向拉出来的几何体。如果这个方向垂直底面，就是正柱体，否则为斜柱体，我们先只讨论正柱体。可能有点抽象，但没关系，比如体积公式我们还是能猜出：$V=Sh$，下面我们就看看具体的几个例子：长方体柱就是超长方体，对吧？我们还有：
返回目录
圆柱柱
底面三维图形是圆柱的柱体：设底面圆柱高为$h_1$，半径为$r$，圆柱柱高为$h_2$，我们可以类比想出体积$=\pi r^2 h_1 h_2$。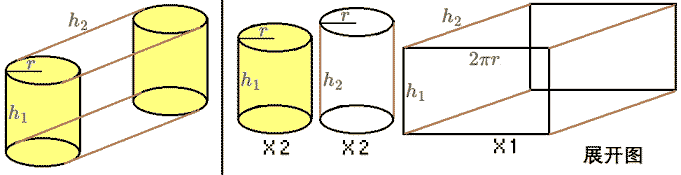
下面来一个挑战性的：圆柱柱的表体积怎么算？它有一个在四维空间中弯曲的三维侧面！我们首先回忆一下柱体的表面积：两个底面加侧面周长乘高$2S+Ch$。侧面积之所以是周长乘高是因为我们能把柱体的侧面展开，即从一处开始沿母线剪开，展开成平面，此时底面展成了一条线。所以圆柱柱侧面也是一样的，只不过是展开成了长方体！
底面：$2\pi r^2 h_1$；侧面：底面圆柱表面积乘圆柱柱高$=(2\pi r^2+2\pi rh_1)h_2$，所以总表面积$S=2\pi r^2 (h_1+h_2)+2\pi rh_1h_2$
- 圆柱柱对称性
不知道你有没有注意到，看了圆柱柱展开图、体积、表面积计算公式后我们都发现，底面圆柱高$h_1$和圆柱柱高$h_2$的地位是一样的，这就暗示我们圆柱柱也像长方体那样可以任选一个圆柱面做底面。别看着另一个圆柱斜斜的，这只是角度问题，转正了看就是一样的了。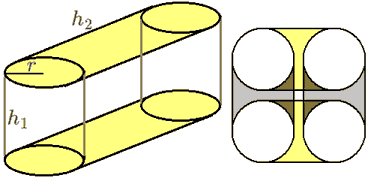
- 《维度》里的老朋友：球极投影
其实用球极投影的方法将四维投到三维只是对很特殊的图形作展示的方法，因为它只是把三维球面$\mathbf S^3$投到了三维空间$\mathbf R^3$，不规则的（如有孔、凹陷、交叉的）图形都无法投影到$\mathbf S^3$上，所以我们一般采用平行投影或透视投影。但我们的圆柱柱还算规则，Let’s have a look look!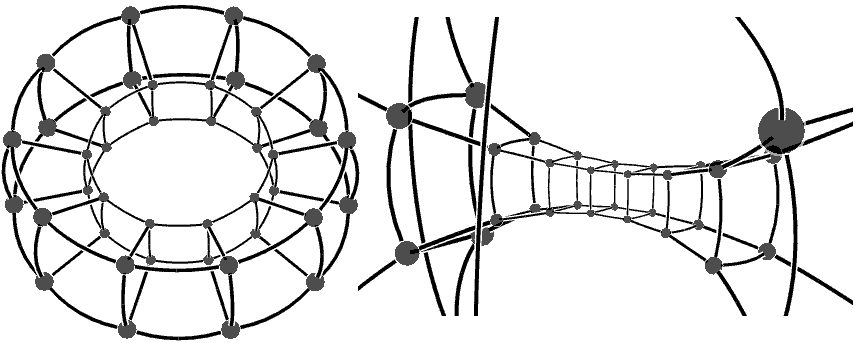
来自jenn3d软件截图
嗯，大圆柱里套小圆柱，就像超立方体大立方套小立方一样。所有柱体的球极投影和透视投影角度合适的话都是大套小。右边换了一个侧面过极点的视角。（其实这是个十棱柱柱，真的圆柱柱是$\infty$棱柱柱）
棱柱柱
从球极投影我们就发现电脑计算圆柱是用棱柱近似的，所以棱柱的性质和圆柱差不多，只不过注意圆柱那张曲面不见了，取而代之的是很多很薄的长方体（比如下图红色那片）组成：$n$棱柱柱由$4$个$n$棱柱和$n$个长方体共$n+4$个胞围成，比如超立方体是四棱柱（立方体）柱，$n=4$，有8个面。
我们怎样计算任意柱体的棱数、二维面数、胞（三维面）数？除了画出来一个一个数，我们还可以从底胞推出来：点动成线，线动成面，面动成体。所以侧面胞数（3维的体）等于底胞的二维面数，都是以对应底胞二维面为底面的柱体（底胞二维面为曲面时会形成“曲胞”：弯曲的三维面）；侧面二维面数等于底胞的棱数，都是一些长方形；侧面棱数等于底胞顶点数。当然记总数时别忘了把上下两底胞算进去。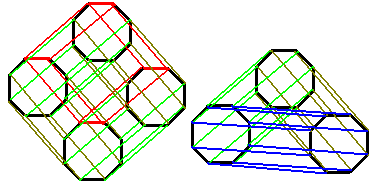
看看8棱柱柱的投影图，感觉就是4个八边形对应点相连得到8个四边形，也能看成由8个四边形对应点相连得到4个八边形。我们尝试点新东西：画一个把3个八边形对应点相连得到8个三角形的东西。这是我们凭空乱画的，这个东西还存在于四维几何空间吗？答案是肯定的，当然这个东西不再是一个柱体了，它可以用直积来解释，后面我会详细介绍。
球柱
它的超体积自然是底胞球体体积乘以高，表面积呢？我们想到自然是底胞球体表面积乘以高。没错，但这里有个小问题：球体是无法在三维空间中展开成平面的，所以它的侧面你是展不开的，也就是说四维空间里的柱体侧面不像三维那样都能展开的！因为三维柱体底面的二维图形总能拉成一条线，但现在却不行了。当然这并不妨碍我们计算表面积，因为我们可以把球微元细分展成无数多小柱体再求和，结果还是底胞球体表面积乘以高。
以后我们还会分析讨论球柱、圆柱柱、超球摆在在四维空间的桌子上里能够如何滚动，直观体会四维空间这个神奇世界。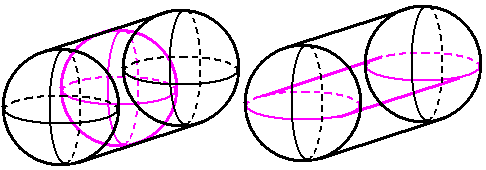
各种锥体
锥体是以任意三维几何体为底面，在除底面所在三维空间的任意地方选一个点，将此点与底面所有顶点连接得到的几何体。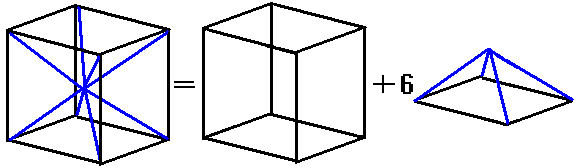
同样，我们怎样计算任意锥体的棱数、二维面数、胞（三维面）数？侧面胞数（3维的体）还是等于底胞的二维面数，但他们都是以对应底胞二维面为底面的锥体；侧面二维面数等于底胞的棱数，都是一些三角形；侧面棱数等于底胞顶点数。记总数时还得把底胞算进去。
锥体的体积和表面积
我上小学时老师和课本是这样讲圆锥体积公式的：把等底等高的圆锥和圆柱放到装满沙子的杯里测体积，发现圆锥恰好是圆柱的$\frac13$，没有任何解释。后来讲祖暅原理和微积分才解释了这个问题。四维椎体计算公式为$V=\frac14Sh$，这是能用微积分证明的，证明略。（$n$维锥体就是$V=\frac1nSh$）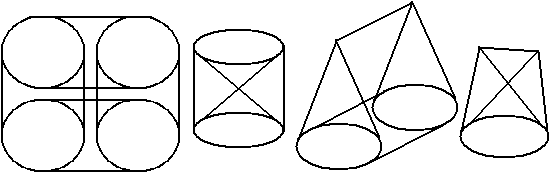
可以想象高维空间一定还有圆柱柱锥锥、圆锥柱锥柱锥柱锥柱等……幸好我们不在那些疯狂的维度！
锥锥柱柱，柱柱锥锥，这个柱锥，你明白了吗？
恭喜你已经有四维文明小学生对几何图形的认识水平了！下一节我们就该学初中的几何了，去看看他们文明中的欧几里德写的著作吧！
注：以前不知在哪看到一篇博文（现在搜不到了，估计是百度空间），由于有“点线面体”，所以作者主张把四维的“超体”取个新名字，叫“太”，超立方体改叫正方太，2维$\mathbf S^1$是圆，3维$\mathbf S^2$是球，4维$\mathbf S^3$“超球”叫“珍”，故超球体叫“珍太”，超球三维面叫“珍体”，这样会较好地避免歧义。我认为这是一套科学的命名法，如果存在四维文明的话，他们应该就是以这种模式叫的。但由于这些名称太诡异，我还是遵从大众的叫法。