四维空间(十):扭结与环扣
我们这次来看一个有趣的话题:四维空间中的扭结。或许大家应该早就知道由于多了一个自由度,三维空间中所有的绳结都可以在四维空间被轻易地解开,所以扭结是三维空间特有产物,四维空间中不存在打结现象,全文完。
我当然不会这样结束这篇文章。虽然一维的曲线无法打结,但是二维的曲面(二维绳子?)却可以打结!我早就听说过四维扭结,但一直没找到具体例子。说克莱因瓶的其实是不对的:克莱因瓶是不定向曲面,如果上面有二维生物,那它们在瓶子上环游一周会发现自己被“镜像”了,而球面上不可能发生这种事,所以这两个东西本质就不相同(不同胚),好比圆环面和球面。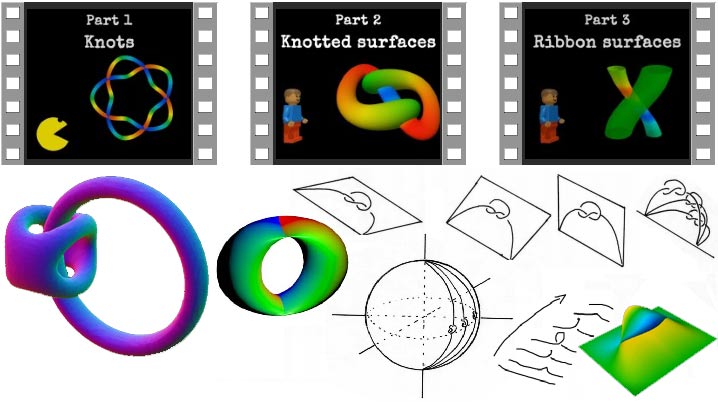
我们先说清楚,到底什么叫“打结”。我不想用数学的语言描述(同痕之类的术语),简而言之就是,从不打结的状态A到打结的状态B,如果不允许自相交的话是不可能做到的,但一旦允许自相交(比如把某些地方撕破)就可以。而且这里的自相交要求局部上是“光滑”的,一般如果再多给一个维度的方向,这种自相交就可以避让。
影片推荐:4D扭结(Knot in 4D)
Youtube上有一个三集的视频详细讲了四维空间中的扭结。我放在了百度网盘里,这是作者的官网,里面还有两个有趣的java的演示小程序。可惜影片没有中文字幕,里面讲述人的英语也很烂(好像是意大利人),我在这里大概再简述一下影片里的内容。
第一集:三维扭结
首先,在数学中,一根打结的线不算结,因为线头可以滑动,结就解开了,所以我们打结后把线两头连起来变成圈,这样无论怎么拉扯也解不开了。怎样表示一个三维空间中的扭结呢?当然是投影。但我们必须注意投影时原来不相交的线会在某些点重叠,为了表明谁在上谁在下,我们有两种表示法:一是把下面的线画成断开状,二是给整个扭结像等高线地图一样上色。我们也将用这些方法表示四维空间中的结。

扭结的中心问题就是给定两个结怎么判定它们是等价的。比如最简单的三叶结和没打结的一个圈(我们也认为一个圈也算结,虽然是平凡无趣的)证明两个结等价很简单,你只需要要把变形的步骤展示出来就行了,数学家Reidemeister归纳了在投影中所有合法的变形方式,称为Reidemeister移动;但要证明两个结不等价很困难,虽然根据生活经验我们知道不用剪刀是不可能把三叶结恢复到圆圈的,但是我们无法证明在无限次步骤之后就可以。影片里又介绍了一种通过计算给投影中的线段上色的方法数量来区分不同扭结的方法,因为上色方法数量在所有合法的变形方式中都不会改变,从而是一种扭结的“不变量”,等价的结的上色数一定相同。
第二集:四维扭结
试想我们拿起一张长方形的布,然后怎么揉了一下就打好了结。但我们只需倒过来做刚才的动作,结就可能被解开。所以数学上的做法是打完结后把布边界拧在一起,变成球,避免滑开。把边界拧在一起是什么意思?为什么不是把长方形对边粘起来变成像甜甜圈的圆环面呢?其实答案是:都可以!你看到了四维扭结的多样性:圆环形是有孔的,显然再怎么允许自相交都永远不与球等价,所以就算是平凡结都有很多种可能。(还有两孔曲面、克莱因瓶、射影平面等)我们先来看看球形结吧。 影片里给了一个把球拉成面条穿过自身的非平凡结,通过高度图我们看到球面穿过自身交叉时两边颜色(第四维的高度)不一样,尝试解开的话中间的绿色会碰在一起,过不去。因为相交的部分三维投影重合了不代表第四维重合,但如果颜色也一样那就在四维空间真正相交了。而到了五维空间,这些二维结都可以轻松解开(因为就算四维的颜色一样,第五维上还有方向可以避开)。类似地,数学家归纳了所有合法的变形方式,影片同样使用计算升级版的上色方法数来证明这个扭结和一个球不等价。
影片里给了一个把球拉成面条穿过自身的非平凡结,通过高度图我们看到球面穿过自身交叉时两边颜色(第四维的高度)不一样,尝试解开的话中间的绿色会碰在一起,过不去。因为相交的部分三维投影重合了不代表第四维重合,但如果颜色也一样那就在四维空间真正相交了。而到了五维空间,这些二维结都可以轻松解开(因为就算四维的颜色一样,第五维上还有方向可以避开)。类似地,数学家归纳了所有合法的变形方式,影片同样使用计算升级版的上色方法数来证明这个扭结和一个球不等价。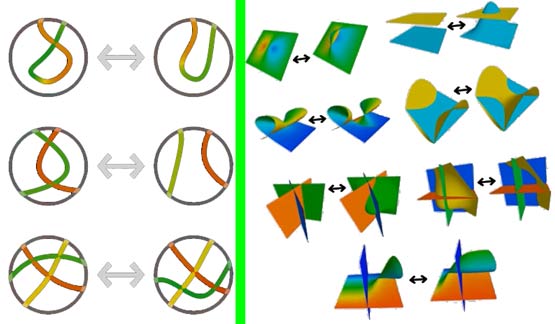
很多合法变形方式都是可以从三维明显类比过去的,但也有两个不那么明显的,那就是含有分支点(Branch point)的投影: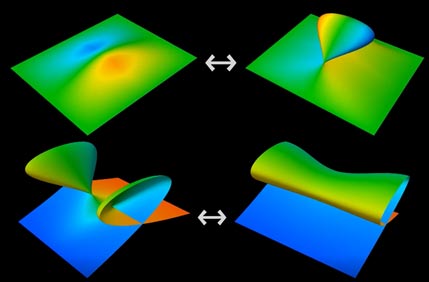
我们通过截面法来展示这两种移动到底干了什么: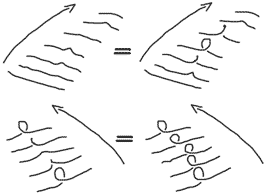
它们的截面变化对应三维空间中一条线的合法移动!(我们甚至可以猜想这两种移动过程对应五维空间中三维曲胞投影在四维空间中的一种合法移动的截胞动画)
第三集:管状结
主要讲的是类特殊的球面结——它们看上去像管子——的线条表示方法。这种表示法相当于一种二次投影。注意只有管子相互穿过自身了才对顺序有要求,而三维空间中的交叉顺序可以在第四个维度上变过去,所以不用表明哪个在上哪个在下。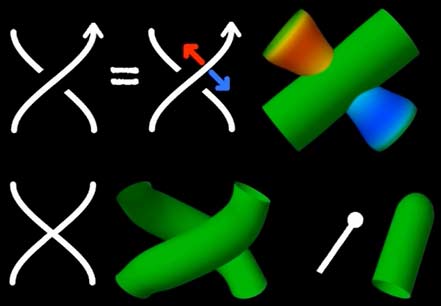
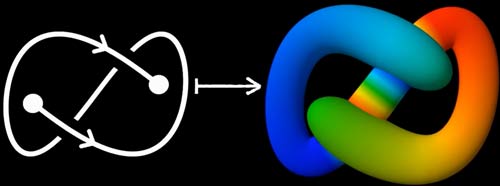
我们可以通过一些变形将一根线上交叉标注的方向变到一致,这样我们就能省略交叉处的箭头了。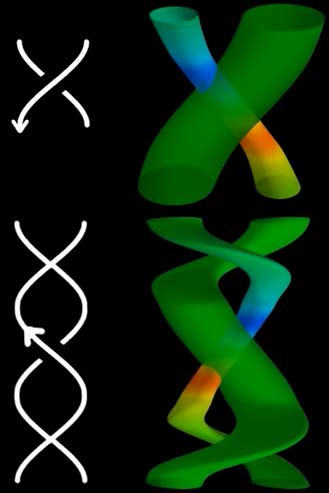
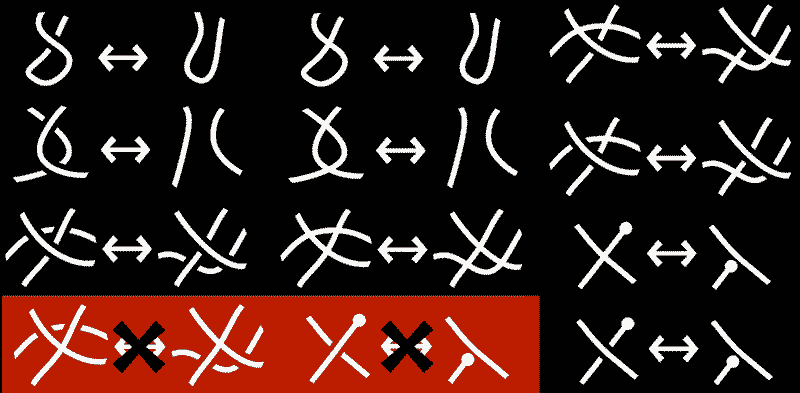
我不能理解的只有左上角给出的合法移动:无法想象穿过自身的管子是如何解开的,或许应该从克莱因瓶的投影中找灵感?
最先我对这方面内容不是特别感兴趣,但后来发现可以把所有的三维扭结通过这些图对应到四维的管状结,给了一种四维人做纺织线不散架的思路!纺织线是一些中空的管线,纺织时不能像三维空间那样直接交叉覆盖上去,而是从管子内部穿过去,就像我们在第二集里看到的球面结那样。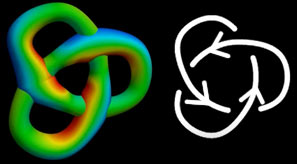
最后影片说到这种方法表示的结太少,比如它不能表示投影中三个曲面交于一点的情况,影片提了一下还有很多复杂的四维扭结,但现在数学家对它们的认识也很少。
形形色色的孔
看完了各种各样的扭结,下面我们来看点不同的东西:由四维珠子串成的项链。按照惯例,我们先分析三维项链:三维项链的珠子是球形的,之所以它们能被串起来是因为每个珠子上都开了一个孔道,这个孔道刚好能让线穿过去;我们能不能在四维超球形的珠子上开孔从而串成一串呢?当然可以。不仅可以,我们还能证明把线两头系在一起后超球就不会掉下来。这个证明可以利用影片中讲到的四维扭结投影上色方法证明。然而我们先要知道开了孔的超球的三维投影是什么样子的。在说明这个问题之前先看看四维空间中其他形形色色的孔。
圆周内部的孔

三维空间中最常见的环扣就是锁链的基本组成单元,这种结构叫Hopf link(没错!就是因为Hopf纤维丛里面扣在一起的圆)。但是三维空间还存在一维的东西吗?其实生活中的圆环是有厚度的,我们换到这个角度上来说,其实是两个圆环面扣在了一起。(这难道也算三维空间的曲面打结?)我们的问题是四维空间有没有类似的东西。首先,把锁链直接拿到四维就散架了,其原理和四维空间没有一维扭结一样。四维中所有物体都或多或少有点四维的厚度,一维的圆加厚就得到球环(我们在上篇文章中讨论过),所以两个球环串起来也会滑开散架,或者说,从圆周(球环)的孔中穿线会掉。我们可以理解为孔的维数比线的维度大,所以穿不上。这种描述或许有点抽象,那有没有更低维的例子让我们直观感受一下呢?
设想三维空间中有个定点,如果一个玻璃球里面有个小气泡(零维孔),刚好气泡把定点包住了,那么这个球就被定点“栓”起来了,不可能扯掉;如果玻璃球有一个正常的一维孔,那么就算定点在孔里面,我们只需要拿着球往孔贯通的方向移动就可以取出来。在继续设想二维孔之前,我们要搞清楚“孔”到底是什么。我们规定:$N$维实心图形上的$n$维直孔($n<N$)是$N$维实心图形挖掉一个$n$维平直的子空间加一点厚度的图形。比如球中间的气泡对应挖掉了一个有厚度的点,有孔的球是对应挖掉了一条有厚度的线。
接下来试着在球面上开一个二维的孔:二维面就像一把刀子,直接将球切成了两半!我们得到的图形不连通了,没有意义这里就不深入讨论了。当然,这些操作得到的孔的周围会很“锋利”,我们的目标是找到典型的光滑的等价几何体。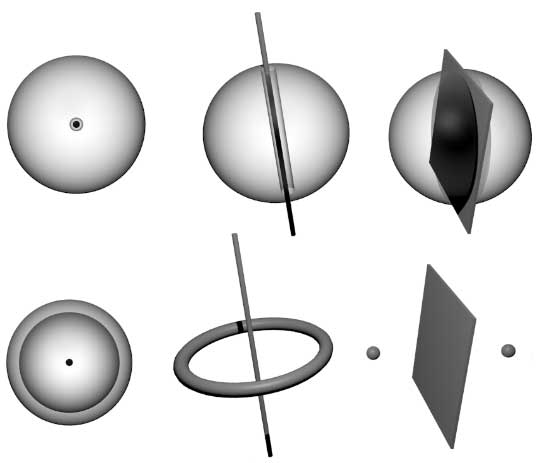
三维空间中各种维度的孔就是这些了。下面轮到四维:
- 零维的孔还是类似于一个中空的气泡;
- 一维的孔是贯穿的一条线,刚好可以穿在线上,但不能包住零维的点;
- 二维的孔是贯穿的一个平面,刚好可以穿在平面上,但不能包住线,可以轻易滑落;
- 三维的孔是贯穿的一个平胞,但它把四维图形切分成了两个不连通的部分。
我们的类比中有一点比较奇怪:用二维的刀片切四维的东西居然没把东西切开!因为多余的维度让在三维空间本该分开的两部分连在了一起!想想二维人类似的悲惨遭遇就知道了:它们没有贯穿体内的食道,因为食道会把它们一分为二,它们用一维的刀片可以切开二维物体,但在三维空间不会,与其说用一维的刀片切三维的东西不如说用一维的铁丝捅三维的物体,最多捅穿捅出个洞来。所以到了四维空间,我们的二维刀具最多只能算二维的“铁丝”而已。
接下来的任务就是去找一些典型的带各种维度的孔的图形。怎么找呢?我们只需要对各种遇到过的图形上的孔分类,以便搞清它们能不能穿在$n$维的“线”上。首先凸多面体、球体、凸多胞体、超球都是没有孔的,三维空间有一个一维孔的东西就是圆环,它的高维类比有很多,比如球环、环球、圆环环、双圆环,这些东西名字听起来应该都是有孔的。首先来看圆周在不同维度上加厚体的洞的维数。把圆周在二维空间里加厚,变成了二维圆环,洞完全在图形里面,可以缩成一点,是零维洞。圆周在三维空间加厚成三维圆环,此时的洞是上下贯穿的一维洞。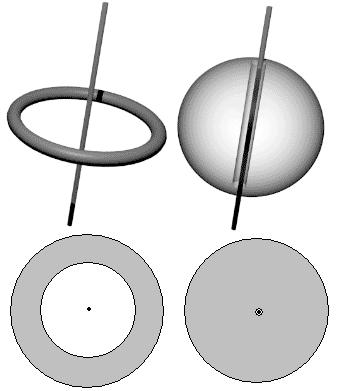
我们看到,洞的维数跟某种自由度有关:设圆周处在$xy$平面上,我们处在圆周中心,沿$x$、$y$轴这些方向上走都会碰到圆周,但沿z轴走就没有障碍,所以三维空间里把圆周加厚得到的物体的洞是一维的,同理,如果空间是四维,沿z轴和w轴走都不会遇到任何阻碍,这就是二维的孔,对应的加厚体就是球环。我们可以明确地标出开孔的走向,但只能通过截面动画这种不太直观的方式来可视化它们(注意球极投影只适合可视化没有洞的凸图形)。
球面内部的孔
现在我们终于清楚了从球环的孔中穿线会掉的原因是因为球环的二维孔固定不了一维线。总结一下就是$N$维空间中的圆周会占用两个维度,剩下$N-2$维就是圆周加厚体孔的维数。如果我们还希望得到一维的带孔图形并要把它们用线串起来,那么就需要加厚从中间往三个方向走都“碰壁”,只留第四个畅通方向的图形。这个东西对应球面的加厚体——环球。同样比较过中心的截面,我们可以看到球环的开孔自由度确实环球大。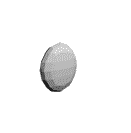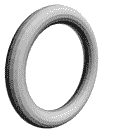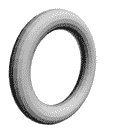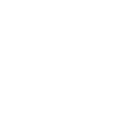
最后让我们梳理一下球环和环球:
- 球环是有“粗细”的闭合的一维图形(圆周),它有着二维的孔;
- 环球是有“粗细(厚度)”的闭合的二维图形(球面),它有着一维的孔;
我们终于找到了可以被线串起来的东西——球环,而真实的线也是有厚度的,但就像我们分析扭结那样,虽然绳子都有厚度,但是我们可以忽略它们,球环就变成了一维的圆周,环球就变成了二维的球面,这样分析问题就简单多了,我们以后将不再刻意区分加厚体与零厚度物体。重述一下就是:二维的球面可以串在一维的圆周上,因为二维球面的孔是一维的,刚好和一维的圆周匹配,但换个角度也说明一维的圆周可以串在二维的球面上,因为一维圆周的孔是二维的,刚好和二维的球面匹配。总结下来就是两个东西相扣,它们本身的维数和洞的维数相互匹配,而且感觉$n$维图形的洞的维数是$N-n-1$维。这个结论其实不成立,我们在后面将看到四维空间中两个二维曲面也能够相扣。
两个球面相扣?
还有一个自然的问题就是两个球面能不能相扣?如果要求球面是刚性的那么是不可以的,因为洞的维数无法匹配,但我们前面就看到了球面自身都能打结,所以两个“软”的球面肯定能相扣(要求每个球面自身没打结)。
同样,三维空间还存在着一个特殊的构造:三个圆圈相扣(Borromean rings),但每两之间都是不相扣的,三个球面呢?
我构造了一种方案,但遗憾的是无法证明它们确实是扣在一起的,因为计算染色方法数得出它和三个分离的球是一样的,当然这也不能说明它与三个分离的球等价,有待用其他判据检验。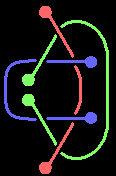
(平)圆环面内部的孔
四维空间有孔的东西还有圆环环和双圆环。它们作为本来就有孔的圆环的旋转体得到圆环环,我们猜测这两个图形或许有两个孔。作为加厚体,它们分别对应四维的平圆环面和三维轮胎形的圆环面。
我们先分析圆环面的孔:首先,圆环本来就有孔,对应圆周加厚,这个孔来源于圆周是空心的,放到四维空间就是二维的,能塞进平面;然后我们只取圆环的表面,得到圆环面,这个操作又是一次镂空。它对应的孔其实也有两个自由度,设想你在环形管道里,你可以顺着管道走也可以往第四个维度走彻底离开管道,只要不往剩下管道壁的两个方向走就行。这个孔可以塞进一张柱面(高的方向垂直于圆环面所在三维胞)。我们看到,四维空间中图形孔的形状开始变得复杂起来。
其实四维平圆环的孔还相对简单些:平圆环是两个空心圆周的直积。如果我们把两圆分别放到$xy$、$zw$平面上并让圆心放在原点,那么平面$xy$、$zw$都不会与平圆环相交。检查平圆环的方程就可以得出来:比如平圆环上的点xy坐标不可能同时为0。
$$
\begin{cases}x^2+y^2= r_1^2 \\ z^2+w^2= r_2^2\end{cases}
$$
如果要用几何的方式解释的话就是:平面中空心的圆周可以看作有零维的孔,它与另一个二维图形直积就是把这个图形在另一个图形上不断平移的结果,这些平移的自由度为二,自然导致了孔的维数升级到了二;根据直积交换律,对另一个图形也是,我们得到了平圆环上有两个绝对垂直的二维孔。加厚后就是双圆环,它从拓补上对应着对着超球捅了绝对垂直的两次二维刀的产物。
我们真的从它的中心斜截面中看到了三维空间类似被垂直的直线捅了两刀的结构!这就是上篇文章中提到的Tiger cage。
最后我想说更奇妙的是,平圆环可以在四维空间翻成圆环,对应的孔也可以连续变形。也就是说我们可以把圆柱形连续变形为平面?这不可能,一定有哪个地方搞错了!其实我们看看三维空间类似的情况就会豁然开朗,没有任何矛盾。
两个双圆环扣?
最后的问题是刚性的双圆环能不能自己和自己相扣呢?我只找到了两个大小不相等的双圆环扣,它的原理是双圆环的一个二维孔套在另一个平圆环面(加厚就是双圆环)上达到维度匹配,但如果两个双圆环一样大就套不进去了,很有可能两个全等的刚性双圆环不存在相扣的方案。
平圆环的三维投影是什么样子的呢?它不可避免会产生自相交(有四个分支点,两条二重交线)。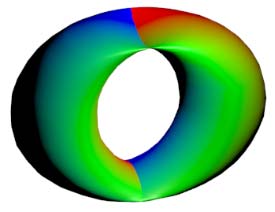
我们的两个双圆环投下来就是:
但通过影片中提到的曲面合法移动方式可以轻松地把大圆环变成标准的轮胎形环面,但由于小圆环套在大圆环上,做移动时要小心自相交的产生。小圆环通过变形也能变成标准环面,那么上面两个平圆环打结就等价于两个圆环面在打结。我们说过这种打结是二维孔匹配在二维面上,所以我们完全不用关心大圆环的其余部分,直接用一张平面表示大圆环的局部。我最先以为等价于如下示意图的管状结: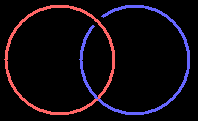
但事实是管状结一点也不万能,这个结无法用管状结对应的图画出来。我们从投影中也能看到,整个小圆环是躺着穿在大圆环面上的,跟上面的图不符。可以认为把双圆环变成圆环时,它的孔从平面变成了圆柱。如果觉得抽象的话我们看一个更简单的例子:球面与环面的环扣可以认为球面与圆环面二维的洞(圆柱面)匹配了,但环面与球面的一维洞是怎么匹配的就很抽象了,因为球面跨在环面的孔上,不能归为简单的对应维度匹配的问题,且管状结也没法表示这种跨越。要理解这个环扣得换用旋转体的思维,我们将在后面讨论。在球面上开个洞变成圆环(洞开在不与其他投影相交的地方,这样就不参与打结),就等价于我们刚才讨论的平圆环扣了,所以这两种结本质是一样的。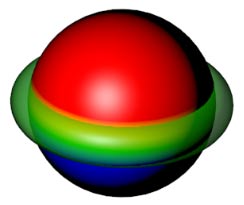
四维空间洞的形状很多,其实三维空间也是,但二维曲面分类定理告诉我们所有定向闭合曲面(除去克莱因瓶这些怪物)都等价于有N个孔的图形,当然这是完全在同胚映射的角度上说的。如果我们把一个孔在物体内部弯成死结,这个孔与没打结的空肯定不等价,但这是在同痕的意义下了(同痕注重变形过程不能自相交,设想允许自相交的话结就解开了)。那有没有三维曲胞(用标准一点的术语叫三维流形)分类定理呢?这个问题太复杂了。但我们之前说过球环和环球的三维表面是等价的,所以可能用一个参数(孔个数或欧拉性示数?)就能表示。三维空间中两条垂直孔相交的曲面等价于有四个孔的图形。所以我十分怀疑开了两个平行二维孔的曲胞和交于一点的二维孔(比如绝对垂直就交于一点)曲胞不等价,很可能双圆环中的两个孔完全就没法变换成其它分离的孔。
扭结旋转体
下面我说说其它扭结。有一种最简单构造二维扭结的方法:设想$xy$平面内有一张方形的纸,把边缘$x$在$xzw$空间中打结,完全不影响$y$轴,这样就得到了以$xzw$空间中的结为底面、高平行于$y$轴的柱体。这种构造扭结的方法叫柱化升维法。除了柱化升维还可以旋转升维。
我们知道,球面由半圆形线旋转得到。那在半圆形线上打个死结再旋转会怎样?好像三维空间都能做到!难道我们发现了三维的球面结?问题出在哪呢?问题在于死结是立体的,旋转时那些本来只是投影重合的点就真的重合了,得到的曲面是自相交的。到了四维空间就可以避免:如果加扭结的半圆在空间xyz中,在三维空间绕z轴旋转的操作到了四维就是绕面zw轴旋转,刚才已经分析了会导致自相交,所以换成绕yz平面转动,这时扭结扫过的方向和扭结本身的空间垂直,就不再有相交了。有人证明了这个曲面也是打了结的。但它拓扑学上还是一个球面:试想允许自相交我们就能把扭结解开,同时对应的旋转曲面也会跟着自相交然后被解开成球。
如果把旋转扭结叫公转,那么扭结在公转过程中还可以自转,得到一些更复杂的有额外“自旋”的更复杂的扭结,想要深入了解可以参考这篇论文。
顺便说下,前面提到影片作者制作的Java小程序上有旋转扭结和带额外“自旋”扭结的模型,另外还有个小程序能可视化所有曲面允许的移动方式,并且标注了投影重叠部分在每张曲面上的位置。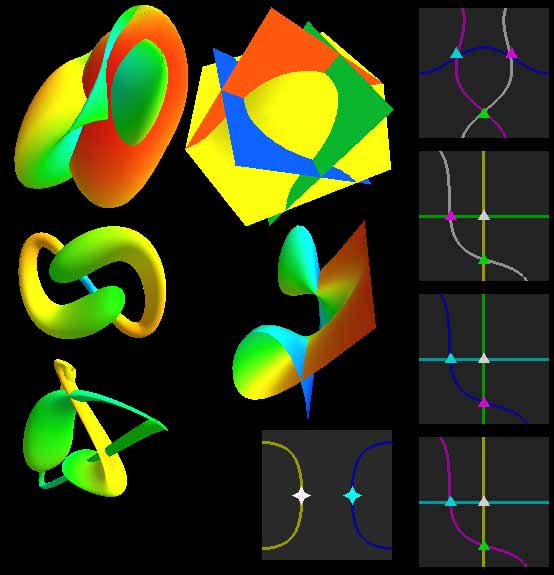
有了扭结旋转体的经验,我们来试着旋转一下三维空间中的锁链,看能不能转出一些新的环扣方式。只要选择锁链所在空间中的平面旋转就能够避免自相交。比如: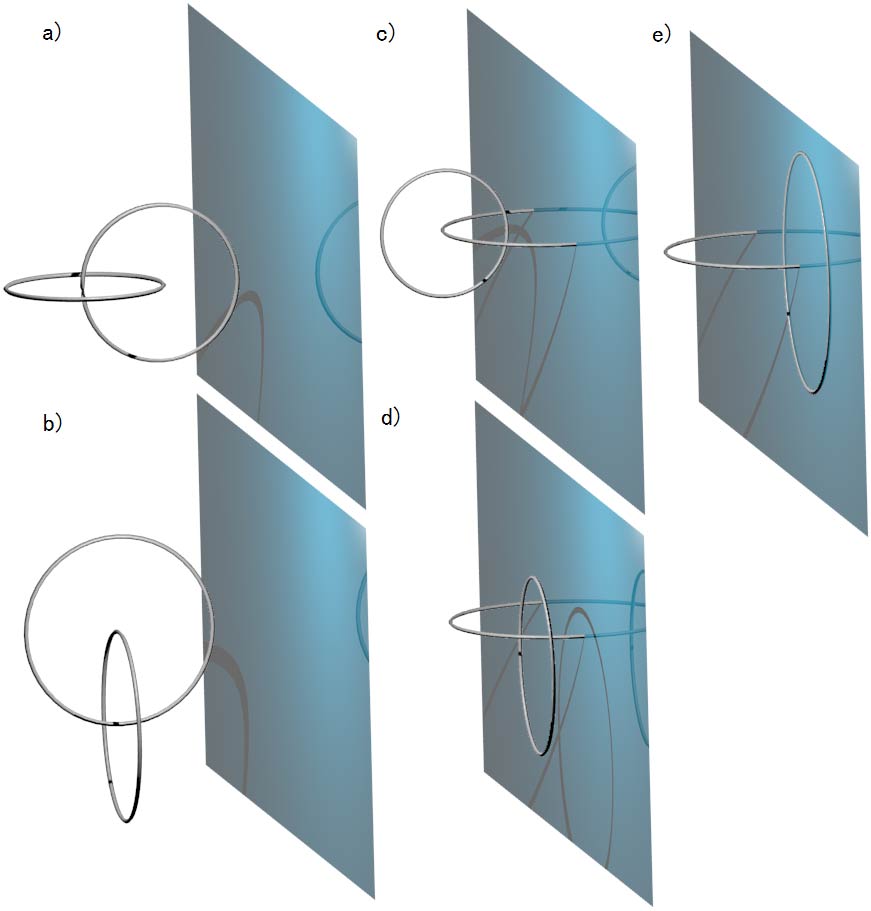
我们分别得到:
a) 一大一小两个圆环面相扣;
b) 平圆环面和圆环面相扣;
c) 圆环面与球面相扣;
d) 平圆环面和球面相扣;
我在这个网站上看到了它的截面动画:
e) 圆与球面相扣(就是我们最先看到的球环-环球扣);
其实我们早就知道如果这些材料是软的的话,圆环面和平圆环面是可以相互变形的,所以不妨把这些东西统称为环面。现在所有的相扣方式就是:除了圆和圆无法相扣(会掉),其余图形都能两两相扣。我们还没提到的有圆与环面相扣。其实圆与任何闭曲面都能相扣,因为二维孔和二维曲面刚好匹配。如果你还是不放心,可以检查一下它们的上色投影: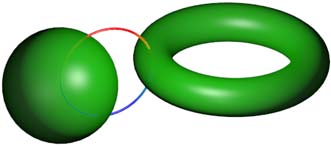
我们看到,圆上不可避免地存在绿色的点,圆环或球不可能从圆上拿开。所以四维空间中的项链也将有两种:一个圈,上面套着一串球面;或一个球面,上面套着一串圆圈。注意这里用“一串”是不恰当的了,因为圆圈可以在球面上自由滑动而不必排成一串。最可能的四维项链是球上串很多小圆,因为考虑到四维人的脖子应该类似柱体(一维线加厚),有着二维孔的圆圈项链怕是戴不稳了。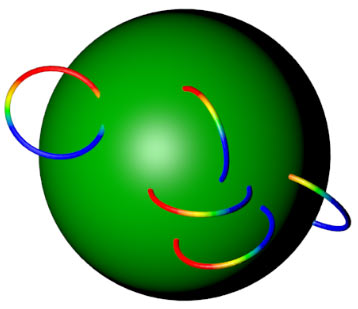
有没有可能那些小圆环也相扣呢?NO!之前说了,三维空间中所有的绳结、环扣都可以在四维空间被轻易地解开,就算投影中发现相扣了,但只用“抖一抖”这串钥匙链它们就分开了,所以圆圈环扣是三维空间特有产物,四维空间中不存在圆圈相扣现象,全文完。
我当然(居然)会这样结束这篇文章。