四维空间(二):超立体几何
#本文讨论的是纯空间上的几何!推荐视频《维度:数学漫步》对四维空间作初步了解,大家还可查看CFY的文章从超立方体说起 作为本文的补充。
今天,我们将接触到更多的四维空间的几何性质、位置关系、更多有趣的四维立体几何题和某些立体几何定理的推广。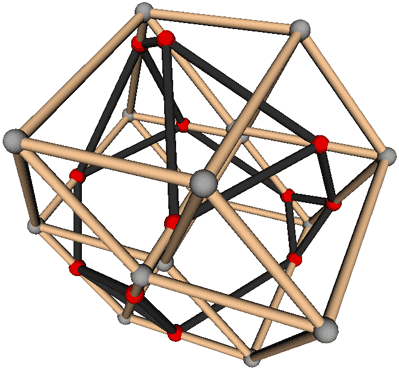
位置关系的判定
两点确定一条直线,三点(不共线)确定一张平面,四点(不共面)确定一个三维空间(或叫超平面)。四维文明初中学的平面几何和立体几何(高中才学吧?)在前两点上和我们学的是一样的。说明只要四维空间中三维子空间的几何问题我们都能解决!下面我们就试着解决一部分简单的四维空间几何问题:判定两几何体位置关系,如果有夹角,求出它的值。
点与其他几何体
- 点与点、直线、平面、三维空间(胞)——点没方向,所以只有在几何体上和不在两种状态。
线与其他几何体
- 线与线——四维空间两条线必共三维空间(想想为什么),所以有重合、平行、相交、异面4种情况。都共三维空间了,夹角当然早有定义,我们也会算。
- 线与面——开始抽象了。先讨论共三维空间的情况:平行、相交、线在面内;线与面有公共点的情况都共三维空间(同样想想为什么),所以还有一种不共三维空间的线与面既不平行又不相交的位置,就好比像三维空间异面直线不平行不相交那样可以把它们平移至相交。既然所有情况都能平移后共三维空间,线面角当然也有定义,也会算!
- 线与胞——是三维空间线与面关系的类比,结论是:平行、相交、线在胞内。线胞角呢?我们规定直线与它在胞内的投影的夹角为线胞角(类比线面角)
胞与其他几何体
面与面的情况很多很复杂,所以我们先看胞:
- 胞与面:面在胞内、面与胞相交于一条线、面与胞平行。面与胞能不能既不平行又不相交?至少四维空间中不能!这就像三维中面与线不能既不平行又不相交一样。
- 胞与胞:平行、重合、相交:交集是一个二维平面
面与面
先说已知的情况:共面、平行、相交于一条线(共胞,有二面角的定义)但两平面还可以只相交于一点:比如坐标面$xy$与坐标面$zw$公共解只有原点!无法想象两无限大平面只在一点相交!
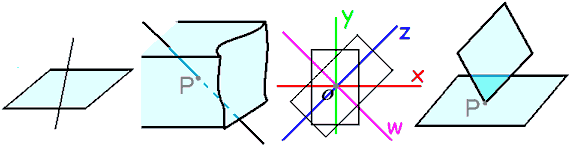
由向量内积可知,坐标面$xy$与坐标面$zw$上分别任给两条直线都垂直,所以我们说坐标面$xy$与坐标面$zw$垂直,但记住它们只在原点相交!这和一般两个平面形成二面角相垂直是截然不同的。垂直角度就是90°,所以这暗示着两个平面的夹角用一个角度描述是不够的!感觉这里有两个自由度!不管怎么说,我们先把两平面上任两条直线都垂直这种两平面的关系叫绝对垂直,以与共胞的二面角垂直区分。
越来越难了,不是吗?到这一步如果不用线性代数理解用硬想的方法求角度就感觉智商不够用了。当我们高中做立体几何束手无策的时候,向量法来拯救我们了,所以下一节我要介绍四维空间中的向量法。注意向量的起点无法确定,我们只能表示方向,所以后文都是在所有几何体过原点的基础上讨论的。在学会系统用向量法之前我们还是得硬着头皮先想想四维空间中的两张平面。我曾经想了很久都没结果,后来终于查到了有关论文:
真相:用两个角度来述
四维空间两平面$A、B$最一般的位置是只在一点相交。我们这样衡量它们的位置:在平面$A$上取遍所有直线$m,m与B$(或$A$)间所夹的线面角会有一个最大值$\theta_1$和最小值$\theta_2$。我们现在用$\theta_1$、$\theta_2$两个角度参数描写平面$A、B$位置关系。
最大最小值?听起来好复杂!或许这样理解要容易些:在平面$A$上作一个单位圆,把单位圆投影到平面$B$上,这个圆变成了椭圆(投影映射是线性的,不可能把圆变成其它图形),椭圆自然有长轴短轴,这两个轴向就是两个特征方向——长轴与平面$A$的夹角就是最大值$\theta_1$,所以长半轴长度为$\cos\theta_1$;短轴就对应最小值$\theta_2$,所以短半轴长度为$\cos\theta_2$。这就是一种叫“单位圆法”的求解夹角的方法的思想,但单位圆法处理椭圆要用线性代数二次型等繁琐的方法。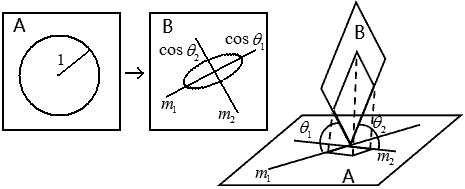
长轴短轴相互垂直,所以线面角取最大值时的直线$m_1$与线面角取最小值时的直线$m_2$相互垂直。但若我们在平面$B$,而不是平面$A$上取遍所有直线$m$得到的两个线面角最值会不会与刚才的值不一样呢?答案是:不管你先选的是哪个面得到的这两个角都是一样的,这保证了定义的良好性。(用线性代数可证,略)
我们先看熟悉的三维空间:
- $A、B$平行:$A$中任意一条直线与$B$的线面角都是0°,所以最大、最小值都是0°,$\theta_1=\theta_2=0$;当然还可以这样理解:这时$A$上的单位圆投影到$B$上是正投影,即大小形状都不变,所以$\cos\theta_1=\cos\theta_2=1$.
- $A、B$二面角垂直:$A$中平行于它们交线的直线与$B$的线面角取最小值0°,$A$中垂直于它们交线的直线与$B$的线面角取最大值90°,所以$\theta_1=90°,\theta_2=0$;当然还有种思路:这时$A$上的单位圆投影到$B$上是一条长为2的线段,我们认为这是长轴为1短轴为0的椭圆。所以$\cos\theta_1=0,\cos\theta_2=1$.
- $A、B$成一般二面角:$A$中平行于它们交线的直线与$B$的线面角取最小值0°,$A$中垂直于它们交线的直线与$B$的线面角取某一最大值(即二面角的大小),所以$0<\theta_1<90°,\theta_2=0$.
由于$A、B$成二面角时$\theta_2=0$,所以我们也叫$A与B$半平行,同时$A、B$二面角垂直我们也叫半平行半垂直,原来的$A、B$平行叫绝对平行。
下面就是四维空间的情况了:
- $A、B$绝对垂直:由于任意两直线都垂直,平面$A$上任意一点投影在平面$B$上都落在它们垂足所在的点(如平面$xy$在平面$zw$上的投影为原点),所以$\theta_1=\theta_2=90°$。
- $A、B$处于一般位置:$90°>\theta_1\ge\theta_2>0$。
- 现在有了绝对平行、半平行、半平行半垂直、绝对垂直,我们肯定会想到半垂直:$\theta_1=90°>\theta_2>0$,这种情况我们后面马上就会看到。
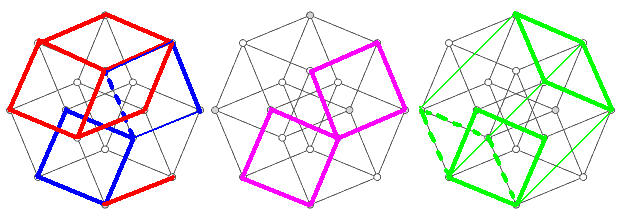
超立方体是认识四维几何最好的朋友
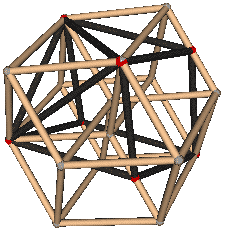
回想高中立体几何,很多线面关系我们都是在正方体里面找的。现在该轮到超立方体了!超立方体平行投影方向很多,但我选的是能反映出四维方体每条边等长,且八个立方体胞全等的投影图。我们将在这幅图上找到几乎所有的几何关系。
这幅图构造巧妙,但也并不难画。先画一个八角星,再以八角星的每条线向外做正方形,将顶点正确链接即可。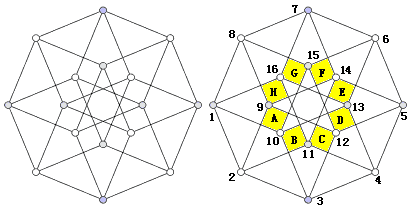
首先,我们得把这八个正方体胞找到。观察一下我们不难发现,只要找到了这些标有字母的黄色小正方形(其实它们并不存在,只因投影时的线条重合),我们就能找到对应的立方体胞。比如黄色小正方形A所对的立方体为9-12-3-2 — 8-15-10-1。以后为了方便,我们就以这些字母代指立方体胞。
不难看出A—E B—F C—G D—H为四对不相邻的胞,它们是互相平行的;顶点之间的距离有四种:1、$\sqrt2$、$\sqrt3$、2。其中距离为2的一对顶点是相距最远的。如1—5、2—6、10—14、12—16。
下面只列举不共胞的位置关系
- 线面关系:异胞(如面2-3-12-9与直线5-6),即既不平行也不相交,可将直线5-6平移至12-15,现在它们相交且共胞于A
- 线胞关系:平行(如胞G 与线3-4) - 线胞关系:相交(如胞D 与线6-7只交于点6)
- 面面关系:共点(如面2-3-12-9与面 12-5-6-15 交于点12,且绝对垂直)
- 面面关系:半平行,但无公共点(如面2-3-12-9与面 14-5-6-7 无公共元素,且半平行半垂直)
- 面胞关系:平行(如胞D 与面1-2-11-16)
- 面胞关系:相交(如胞D 与面14-5-6-7交于线6-15)
- 胞胞关系:平行(如胞D 与胞H)
- 胞胞关系:相交(如胞D 与胞E交于面 4-5-6-13)
其他
你可能会说我找的都是正方形面,没意思。好,现在我们找一些有趣的超立方体的截面和“斜着的面”的位置关系。
超立方体截面
验证四点确定胞:在超立方体里任选四个不共面的顶点都可以确定一个胞。就像我们做立体几何体一样,有时这四个顶点组成的四面体胞并不是完整的超立方体中的截面(注意,这里是三维的面),我们可以“补形”,将其截胞补充出来。如点1 、点15 、点9 、点13(红色标出)所确定的胞(设为胞$\Pi$)就需要“补形”。我们注意到顶点9和顶点13是一组相对的顶点(即距离最远,为2)则线段9 13过超立方体体心(暂记为点O)。所以胞$\Pi$过点O。而点1与点O所在直线也该属于胞$\Pi$,又因为点1、点O、点5共线,所以点5也属于胞$\Pi$。类似地,我们可知,点15、点O、点11也共线,则点11也属于胞$\Pi$。(补出来的点用黑色标出)把这些点连起来(注意相对点不能相连,因为连成的体对角线在超立方体内部,不是截面的边界图形)。再计算一下我们发现,除了这些相对顶点之外,其余任何两点之间的距离均为根号二。这说明胞$\Pi$与超立方体八个胞都相交,得截超立方体为一正八面体胞。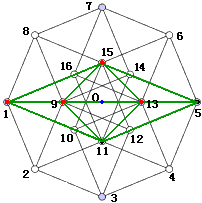
怎么确定你的形状补完了呢?如果你的所有截胞图形的面都在超立方体表面上——八个立方体胞内——即所有棱都在超立方体的24个正方形面内,说明补形才算完。
在超立方体里任选四个不共面的顶点可确定的胞的形状很多,这里我把它们在下图左边罗列了一部分:分别是(1)对角胞(如1-8-15-5)(2)正方体胞(如5-7-8-15)(3)截角产生的正四面体(如1-11-13-7)(4)最大截面正八面体(如1-7-9-13)(5)截棱产生的三棱柱(如1-2-4-7)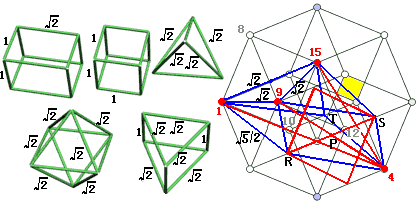
但这里值得我们一提的是在超立方体里任选四个不共面的顶点确定的胞补形后补出的顶点可能不是超立方体的顶点,比如右上图点1、点9、点4、点15所确定的胞$\Gamma$。补出的三个顶点居然是棱的中点!具体补法:因线段4-9过胞C中心点(暂记为点P)过点P作平面平行于面1-8-15-10 交胞C于一正方形(粉红色标出),其中产生了R、S两点。则点R(线段2-11中点)、S(线段12-5中点)在胞$\Gamma$内。原因:∵RS∥线1 15,∴R、P、S、1、15共面。∵1、15、P在胞$\Gamma$内,∴R、S也在胞$\Gamma$内。而补出了R、S点,剩下的T点用做平行线的方法也就不难补出了。最后我们来观察一下这个完整的截胞。这是有着三个边长为$\sqrt5/2$的菱形,一个边长为$\sqrt2$的正三角形,和三个等腰三角形构成的七面体。有七个面,说明胞$\Gamma$与七个胞都相交,而有一个胞没有相交,那就是胞E(这里单独用黄色表示)
斜着的面
- 绝对垂直
请找出找面1-3-13(下图左边的红色面)的法平面。
思路:只要我们找到两条相交直线都垂直于这个平面,则那个相交直线确定的平面就绝对垂直与这个平面。(这是绝对垂直垂直的很好的判定方法哦)
因为面1-3-13在胞B内,所以我们不妨在胞B内找一条面1-3-13的法线,即10-11(立体几何三垂线定理不难得证),那么直线10-11即为一条我们要找的直线。
而胞B垂直于线10-15,所以在胞B内的面1-3-13也垂直于线10-15。这样,由线10-15、线10-11确定的平面10-11-14-15即为所求法平面。(蓝色面)它们的唯一公共点在线段10-11上靠近10的三分点处。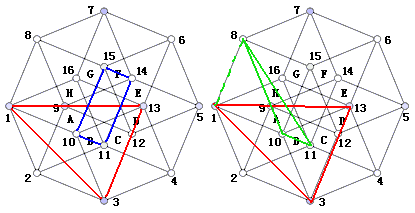
- 半垂直
如上图右边所示,面1-3-13与面10-11-8半垂直:直线10-11垂直于面1-3-13,但点8在面1-3-13上的投影为1,显然没落到它们的唯一公共点上。所以点8与公共点的连线不垂直于面1-3-13。所以这两个平面半垂直,$\theta_1=90°$,但我们怎样求出$\theta_2$的值呢?它是一个最小值,感觉怎么都从图上看不出来。
好像现在继续往下走行不通了。但回想一下高中的立体几何,好像在求两平面夹角(当然是二面角)时老师还讲了一种方法:射影面积定理。
思考题:请画出右上图中绿色平面的法平面(绝对垂直平面)
射影面积定理的推广
射影面积定理是平面图形射影面积等于被射影图形的面积S乘以该图形所在平面与射影面所夹角的余弦。
这是我们三维空间中熟知的。下面给一个大概证明思路:
我们在选一种特殊形状的被射影图形:正方形。位置也很特殊:正方形一边选到平行于两个平面的交线,另一边自然就垂直与此交线。投影后平行于交线的边长度不变,垂直与交线的一边变成了$\cos\theta$倍,其中$\theta$是两平面二面角,所以正方形面积变成了$\cos\theta$倍。我们把其他不规则形状划分成无数这样小的方格,所以整体面积也满足$\cos\theta$倍的关系。
四维也一样,只是选正方形面积元投影到两边在夹角最大值方向和最小值方向上(还记得吗?这两个方向刚好垂直)都要乘上角度的余弦值,导致面积变为原来的$\cos\theta_1\cos\theta_2$倍。即:
四维中射影面积定理是:平面图形射影面积等于被射影图形的面积S乘以该图形所在平面与射影面夹角$\theta_1、\theta_2$的余弦的乘积。
我们用这种神奇的方法都只能得到$\cos\theta_1\cos\theta_2$,显然还差条件。看来必须用代数才能求夹角了。后面我们将看到向量法也不再适应四维几何,向量法需要被改造,在改造的向量法中我们还需要用到射影面积定理的推广。