四维世界(五):体验四维人的视觉与方向感
特色内容
- 3D体素在线查看器
- 多胞体图形库浏览器
- 4D第一人称小游戏
在上一期的文章中,我们讲到了二维人怎么看我们世界的照片,而今天一个自称生活在四维空间的神秘人与我们电脑建立了连接,它说,它们的四维双眼的视网膜是三维的,能直接一口气看到三维的图像,而且它将传输给我们四维世界的3维的画面,并专门为我们设计了一个查看这些三维图形数据的查看器!(最好用电脑谷歌浏览器打开获得最佳体验,如果你用手机的话可以先看看查看器的截图)之前大家看到的四维模型大都是以线框形式画出的,可能还不太适应这种3D体素上色的方式,因此四维神秘人首先向我们发送了一些纯三维的图形作为训练,以防我们看到四维照片就直接懵圈。
三维照片
还记得上一篇文章中的二维生物吗?它们先后用了透明照片法和截线法来观看二维图形。我们将同样采用透明法和截面法来观看三维图形。以下是这些截面的抽取位置,为了以后表述精炼,顺便约定一下这些截面怎么称呼: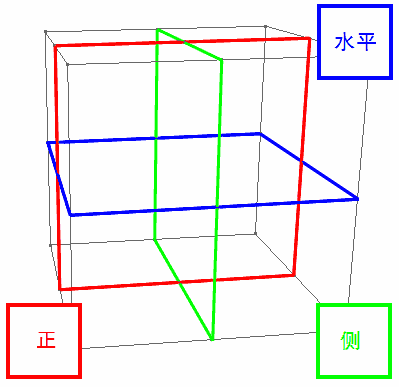
比如下面这个是:我们三维世界的普通鸡蛋。点击下面图片进入查看器(我不直接嵌入进是因为一个页面太多3D会很卡),直接使用键盘W S A D Q E上下左右前后移动,用鼠标左键拖动来旋转,中键右键拖动也能移动哦。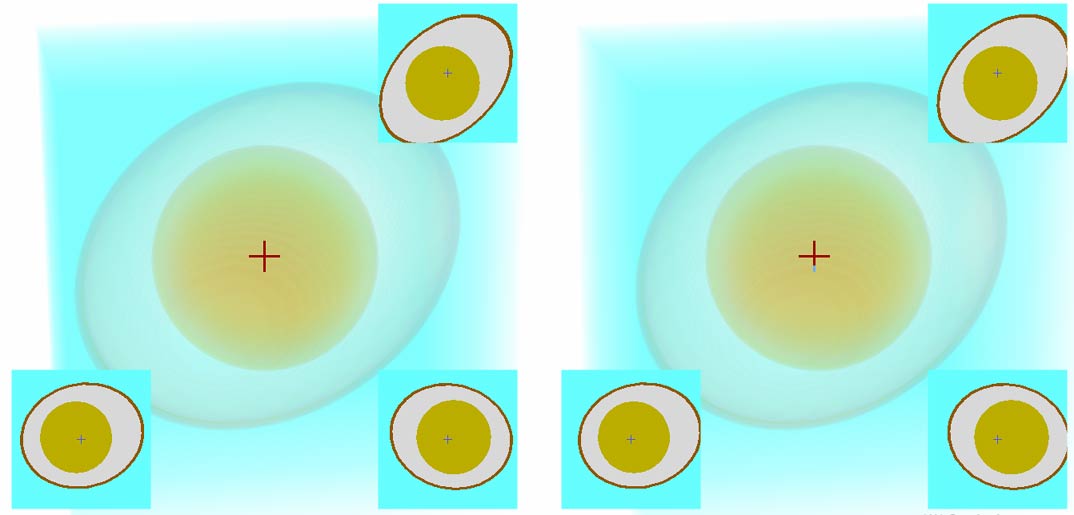
下面我们来解释一下这个图的意思。左右两幅图通过模拟左右眼来产生立体感,让你更好感受到这张照片是三维的。如果你不会看这种裸眼3D的化,那就请来回按左右方向键吧(但体验确实会差很多)。整个鸡蛋被做成了半透明的,能够看到里面的蛋黄。对,我们现在也有了透视三维世界的能力!当然,这种透视是因为我们半透明化了这些3D像素,但我们可以在旋转着查看并且还综合了截面等信息脑补出这张三维图像中每个角落的颜色,你可能会说,这就是一个透明化的鸡蛋,这算什么四维超能力呢,但我们要从现在起,假装能够“一口气看到”正方体3D视野中的每个像素(体素)。
我们假装自己能看清的代价就是实际上并不能看清一些细节。比如你很难从三维透明照片上直接看到鸡蛋蛋壳。所以四维人为此专门设计的抽取截面还是很有必要的。
注意这个鸡蛋完完全全就是三维的物体,没有任何四维的东西在里面,这只是个三维体素查看器。我们首先要训练自己习惯这个三维体素查看器,要尽量建立起立体直觉,因为之后所有四维景观都要在这个三维体素查看器中显示出来。
四维照片
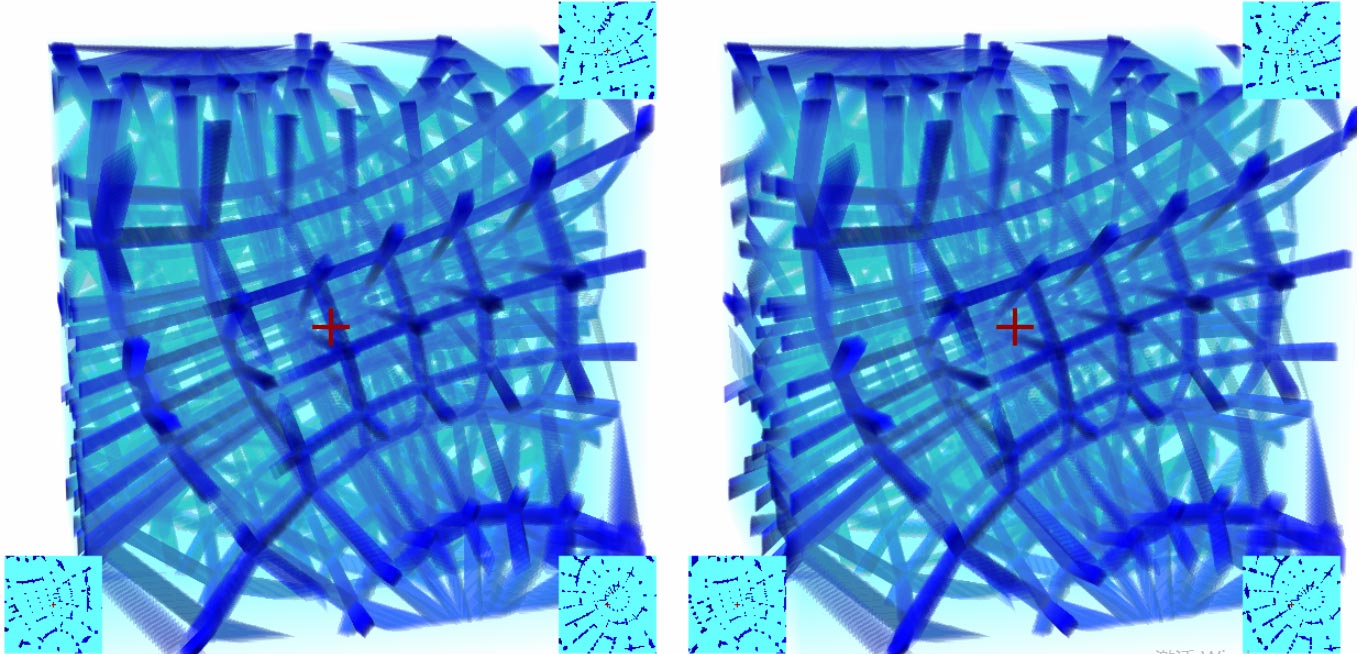
接着他发了另一张立体图片,他说这是一个每个胞上画了一个球的超立方体。这次我们将摄像机固定在超立方体中心,虽然不能自由移动(主要是怕迷失方向),但可以像看鸡蛋那样旋转这个照片。点击下面图片进入查看器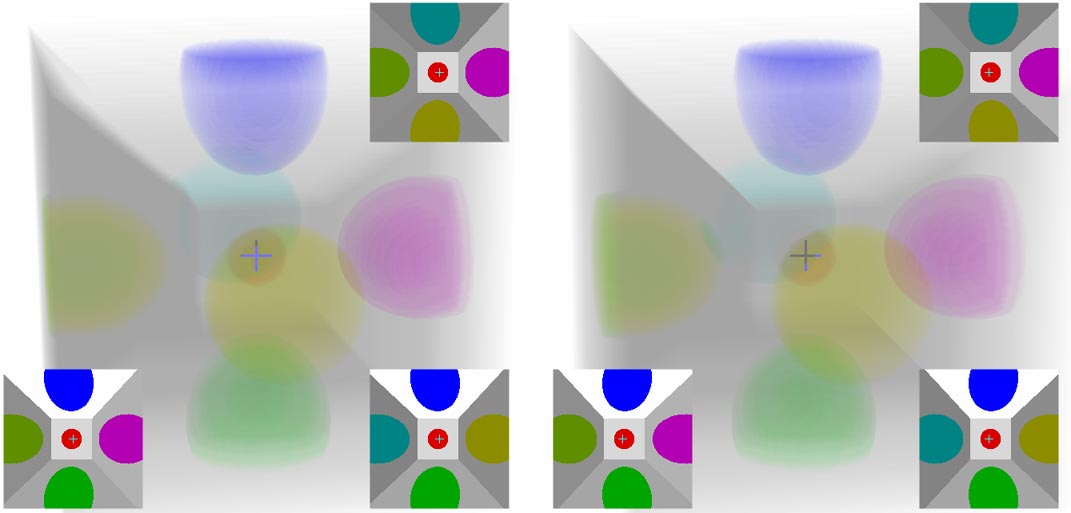
我看到了什么?
我们不难看出视野里有七个面,最中央是一个完美的立方体,它的六个面向外接着一些棱台形。跟下面正常的立方体照片对比一下应该是不难理解的。,视野有五个面,最中央那个是完美的正方形,周围四个梯形。旋转超立方体后,可能某些胞中心的球形图案不再与截面相交,所以你会看到这些球体忽大忽小时有时无。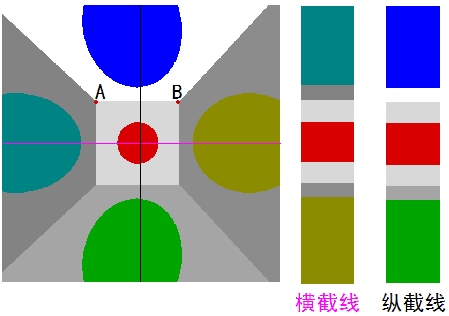
注意四维物体能直接被看到的东西都是三维胞(我们管三维面叫“胞”,以与二维面区分),二维的面不再有确定的颜色,它们只是四维物体的一种二维的棱角。类比到三维就是你无法说出上图中线段AB的颜色。还有一个有趣的现象就是,三维世界中,无论一个塑料薄膜有多薄,只要它是不透明的我们正对着它就能看见它,但拿到四维去就不行了,无限薄的塑料薄膜在四维人视野中的体积接近于零导致无法被看清。降维类比就是:头发丝是不透明的,但太细则无法看清。
走进四维
这时四维人告诉我们,这张图不只是一个静态的图片,你可以用右键、中键转动这个超立方体看它的各个面!注意之前左键的转动只发生在3维视野内。你甚至还可以滑动鼠标滚轮,让摄像机从超立方体内部钻出来!在外面看超立方体我们一次最多只能看到四个面,你能找到那个角度吗?点击下面图片进入查看器
我对超立方体做了什么?
- 当你用左键拖动时,模型在三维空间中旋转:你仅仅是转着角度看三维的体素,视野中的3D画面组成是没变的;但由于三维的体素旋转后可能不再在截面上,所以截面上的二维画面会不断变化;这种旋转类比到二维也是直接旋转照片本身:

- 当你用右键拖动时,模型在四维空间中旋转:你的实际四维空间的摄像机位置朝向会改变,此时组成三维画面的体素会变,具体体现在本来中间的小球体会变形成在侧边的大而扁的椭球形;但此时你会发现一些截面上的画面变化更像是换着视角在看一个普通的3D物体。这种旋转类比到二维也是一样——正方体旋转时本来中间的小圆会往侧面大而扁的椭圆移动,另一边侧面的椭圆会变小往中间靠:

体验四维空间深度
现在我们能够直接体会到3D体素画面的立体空间感,但还是无法对四维建立起直观感受。我们来看一看到底怎样才能得到完全的“四维空间感”:(如果你不会裸眼看3D的话,这个四维空间感可能是无法体验了,除非以后开发VR版的查看器)
你坐在二维的显示器前,图像上每个点都有二维的坐标$x$、$y$,加上左右眼的立体视觉与透明化像素处理,你能大概知道每个点的$z$坐标。$x$、$y$、$z$三个坐标即3D体素显示器上的像素坐标,也就是说但从看3D照片这一点来说我们已经做到了。但要想更直观了解四维,我们还需要拥有四维人的左右眼超立体视觉:即感知每个体素的第四维深度$w$。四维人的左右眼超立体视觉又是什么呢?其实原理也一样:通过左右两个摄像头(或四维人的眼睛)拍两个3D照片,四维人的大脑就能产生第四个方向上的深度感。
很遗憾我们大脑最多能通过想象分析脑补一维(为了看到3D照片我们已经用掉了),再补一维是怎么都塞不进去了。怎么办呢?一种解决方式就是让立体深度感的那一维交替使用:之前我们把它分配给了3D照片的$z$方向,我们也可以分配给第四维的$w$深度,只要不一起冲突就好。但立体视野本来就是3D图像,我试过直接显示四维空间拍摄的左右两张3D照片作为左右画面大脑是无法处理里面的信息的,所以最好的办法就是让第四维的$w$深度在单独抽出的截面上显示,所以你之前看到的不同部分的立体深度表达的含义是不一样的,现在我们以一个超立方体框架为例来说明: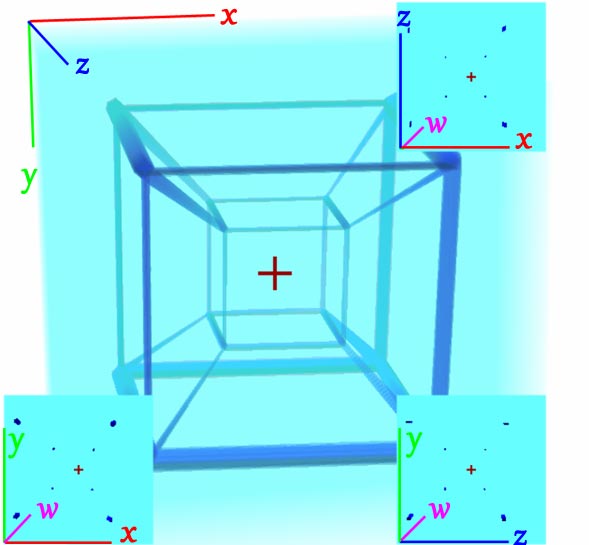
请问小立方体是否在大立方体里面?
稍微了解四维的人都知道,小立方体只是四维投影到三维的透视现象造成的,其实它们一样大,但小立方体离我们更远,所以看起来小。但它投影在三维照片上的确在大立方体里面。这里的立体视觉也给我们提供了大小立方体嵌套的感觉: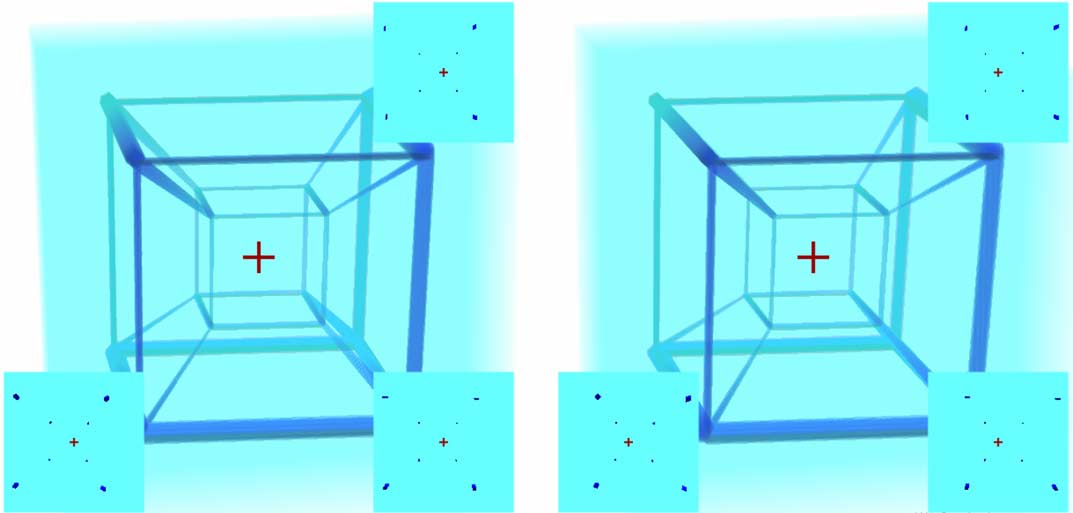
我们再来看三个截面。由于截面截棱得到点,所以三个截面能分别截到大立方体四个点、小立方体四个点。而左右两个截面视差被设置为第四维的$w$深度,所以我们看到了小立方体确实在大立方体的后面。虽然只能知道截面处的第四维$w$深度,但我们可以通过平动、转动等方法让所有像素都被截面扫一遍。我承认这种方法并不直观,但是目前最折中的结果了。
看看其他各种多胞体
下面我们来看更多复杂的四维多胞形:点击下面图片进入多胞体库查看器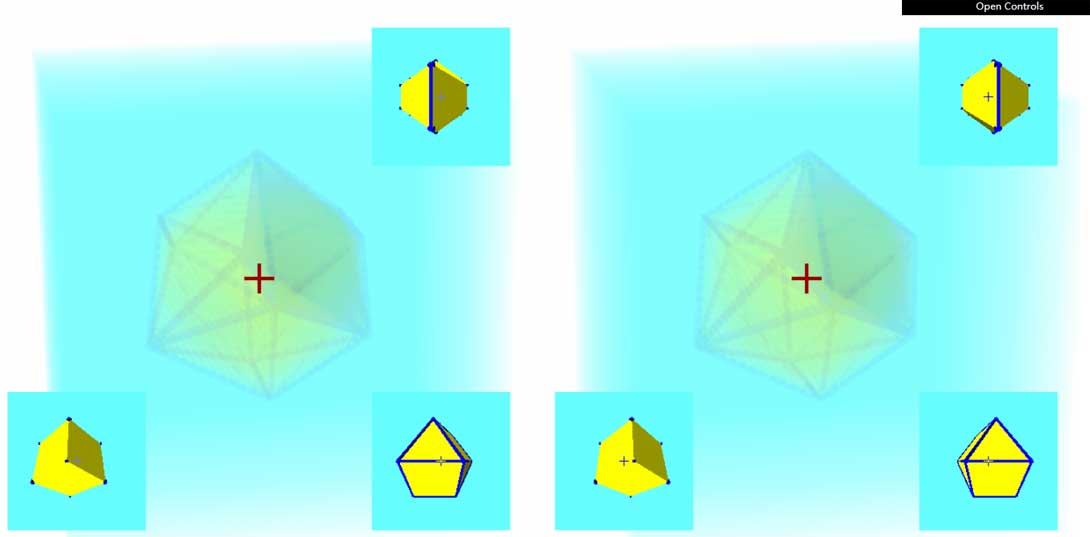
点进去是一个从外面看到的正二十四胞体。也可以滚动鼠标滚轮到内部观看。(从内部看其实有点看球极投影的感觉)
点击右上角的“Open Control”可以展开快捷栏,你可以在选择形状下拉菜单中切换观察各种几何体。比如圆环柱:
首先在选择形状下拉菜单中选择柱体
在柱体栏的底胞下拉菜单中选择圆环
视图中出现了一个8边形的圆环。调节圆环栏中的U、V值能改变分段数,分段越高圆环越光滑,但会更卡。
由于圆环柱是曲胞图形,所以不用显示随分段数增多而异常凌乱的棱,它们很消耗渲染资源造成卡顿。选择显示->胞来隐藏它们。
如果你觉得蓝色背景颜色迷雾太重,可以展开Render栏,降低bgColor4Flow的值;同样如果觉得几何体太过于透明,可以增加Flow值(增加Flow值将会让几何体与背景的不透明度一起增加;所以需要配合降低bgColor4Flow)当然,如果你觉得这些设置太复杂,你还可以直接选择预设下拉框中的胞(除雾)选项。
通过调节高来改变柱体高度,我们可以把这个值调高或调到0来观察比较。
如果你觉得3D视野显示有很多粗糙的锯齿,请按大键盘+ -来调节3D视野$z$轴分辨率。3D视野的本质是很多层截面叠加起来的,截面越多分辨率越高运行越卡,所以请谨慎调节。
我该如何理解这些形状?
如果有完整看过我之前的四维空间系列,想必你对这里面大部分几何体都能够理解(至少是逻辑上的推理性理解)。我相信你们对这些图形并没有任何直觉上的理解,但我们不妨通过分析来搞清楚我们看到了什么。
还是以圆环柱为例子。首先我们把柱体->高设置为3,得到一个长长的圆环柱空心管子。如果你没旋转过视图的话会看到这样的图形: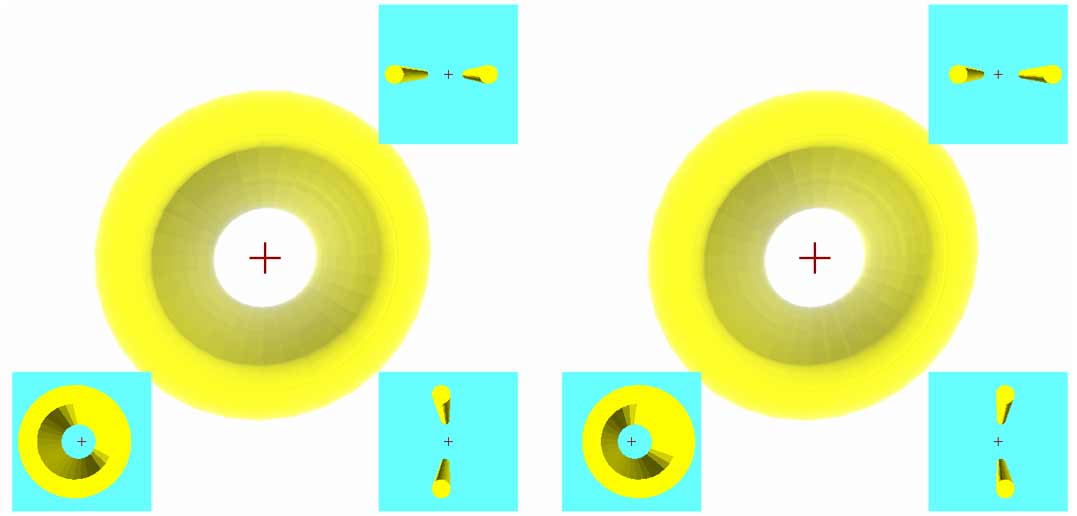
什么?你说看不出来是管子?我们用鼠标右键水平方向拖动转一点点方向:
我们注意到3D视野里的图形几乎是无立体感的,说明这个东西在$z$轴上很薄。通过看右下角的$yz$侧截面也能看出它$z$轴上的厚度只是圆环的小半径。通过左下角的$xy$正截面、右上角的$xz$水平截面能明确看到这是一个柱体,且高的方向为$w$方向。截面中也是两个三维的柱体,但柱体的底面却是圆环的截面……
其实你说它是管子也不太对,虽然左下角的正截面上它是封闭的,但从右上角的水平截面截面上就能够很清楚地看出这个管子完全不封闭,水会完全漏走。如果四维人真要做水管,它们应该选类似球壳(即空心球)柱这样的封闭图形。
如果回到最开始的正视图,使用鼠标中键拖动则会直接在3D视图里看到一个圆柱:这也是一种侧视图。
多胞体图形库里还有各种图形都可以尝试。但有几点要注意:
- 某些面数较大的图形可能较卡(比如超球),建议关闭渲染棱(显示->胞)。但如果确实想看棱的话可以按
C键开启线框模式。线框模式下默认的$z$轴层叠分辨率不够,按大键盘+适当增加一点分辨率即可。 - 如果觉得截面视图太小或太大,可按
;'调整。 - 更多快捷键可以参考这里。
你现在可能有点晕头转向。记住当你每次对画面不理解的时候都应该想想有没有类似二维生物看三维的对应窘境,有时这种类比会让你豁然开朗,因为你会发现原来你从不同角度看三维物体都是靠大脑天生自带的“显卡”就处理了,一切都是瞬间直觉,但当你来到四维空间后你反而可以经过大脑(“CPU?”)倒过去想为什么物体会是那个样子。
当你对四维的画面足够熟悉后你会发现你渐渐不再需要每次分析各部分图形形变,也不用通过低维类比来理解时,你对四维空间的新直觉就建立了。下面是各维生物认识高维的流程图: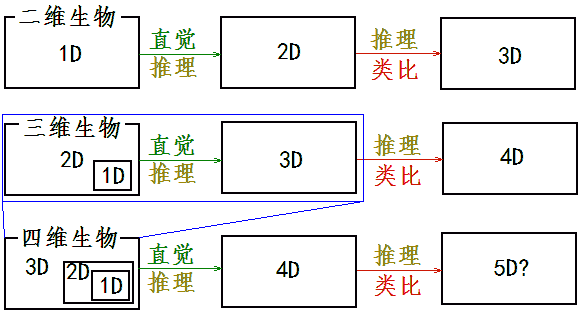
在四维世界中散步
熟悉完基本的单一几何体后,四维人终于邀请我们进入了四维世界。
这个世界上有重力,所以有上下方向;我们将你面朝的方向记为前方(也就是垂直于3D视野图的四维深度$w$),相反的方向是后方。在三维世界中,同时与上下、前后方向垂直的方向就是左右方向,但在四维,还剩两个垂直的方向无法确定,于是我们只能先强行按下图规定左右方向与一种新的方向。但这种新的方向的性质跟左右一样,本质上也是一种侧面上的方向,这里说前后只是它是3D立体照片显示器的前后方($z$方向)。所以本文称之为“侧前”与“侧后”方。
你可以以第一人称视角自由移动。下面介绍一下控制操作:
使用W S A D前后左右平移,新的侧面方向(3D视野的前后)使用Q E平移,按住空格键升高,松开后会在重力作用下掉回地面。鼠标上下左右移动或U O J L可以环视六周(注意四维有六“周”而不是四周),分别对应向侧前、侧后、左、右环视转向。最后鼠标滚轮或I K键控制抬头或俯视;按Z X可旋转三维视野图像,按C可以显示棱(其实画的是每张截面的顶点),以便在模糊的透明图像中看清物体的轮廓。点击下面图片进入:
你能在不使用跳跃键作弊的情况下爬上斜坡来到平台上并穿过四维隧道吗?如果有困难的话下面就说一下我习惯的步骤以及思考方式:
- 首先我先按
S键后退来观察一下周围。 - 在右下角截面中我看到了斜坡,所以我想先调整位置对准斜坡然后上去。
- 右下角侧截面是$yz$方向截面,其中横轴是$z$方向(侧前侧后方),纵轴是$y$轴重力方向。我要往右走,对应侧前方,所以按
E键移动对准坡道。你会发现对准坡道后左下截面的也会出现坡道。按W前进,爬上坡顶。 - 用鼠标环顾六周,同时注意看右上视图,当你看到一个开洞的大长方体后,用十字准星瞄准这个洞,此时你会在其它两个截面看到隧道。
- 调整方向进入隧道。这个过程中你应时刻注意下方每个截面你是否离路边缘太近,不断调整防止掉下去。
- 进入隧道后如果无法继续前进,说明你已经碰到墙壁了。此时注意看右上截面,能够明显看到你碰到了方孔壁。用鼠标重新对准方孔中心前进即可穿越隧道。
- 挑战成功!
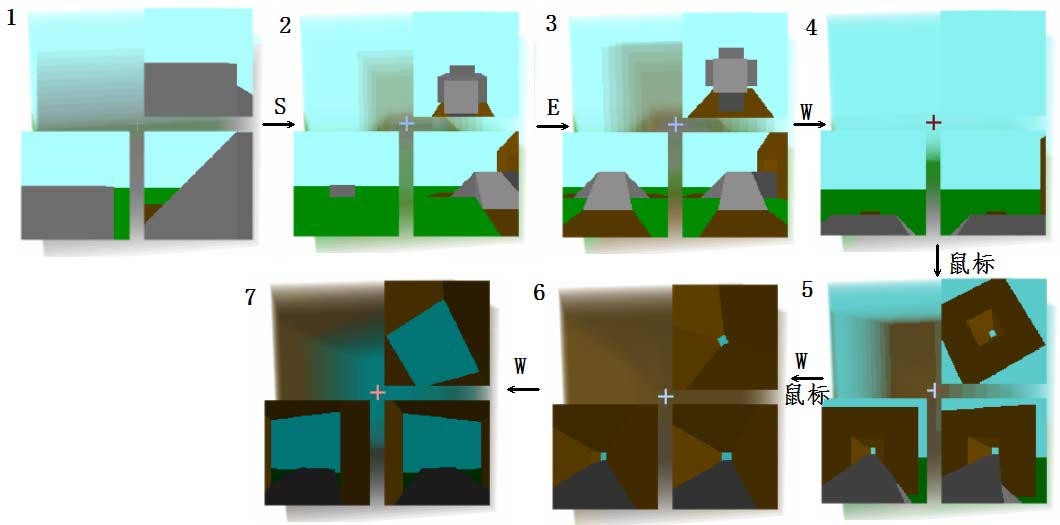
以上过程全程只需看截面,没有看立体视野。如果你觉得这是作弊,那么我们就来挑战只看立体视野通关。按;键将截面视图最小化。由于立体式样重叠太多看不清,所以我们按键盘C显示线框。同样我说下我的思路:
- 首先我还是先按
S键后退来观察一下周围。 - 我发现左、右、侧前方都有往上走的坡道,但侧前方那个最大,应该距离最近,所以应该按
E键往侧前方移动,让往侧前方斜着的四棱台变成向下的正棱台,然后就能往上走了(不理解?请看这里)。但我不想跟之前的路线重复,我偏偏要走远的——从左边的坡上去,所以我按A往左移动对齐到坡底的位置。 - 按
W前进到坡的位置; - 但这个位置没有标志物不太确定,我们只能走得感觉差不多了往右转,看自己对准坡道了没;
- 右转后发现下方的棱台不正,往侧后放偏,按
Q移动调整; - 总感觉离坡道太近看不清棱台地步是否对正,于是按
S后退观察; - 此时发现下方的棱台往左偏,按
A移动调整; - 对好后按
W前进往上走; - 往前走,看到了上面的路面刚好露出来,说明人眼睛高度跟上面平台高度一样,坡道还上没完,继续按
W往上; - 往上走直到感觉高度不再上升马上停止(以免过冲下去);
- 侧前方视角边缘已经露出了方形东西,故用鼠标朝那边看,观察有天空颜色的小块,那是洞穴另一头的天空。注意路面棱台一定要保持在正下方,不能往左右或侧前侧后偏移以免摔落;
- 对准洞口按
W进入隧道,同时鼠标不断调整方向,保持洞口天空对准十字准星(左右、侧前侧后方均要对齐),否则会碰壁。
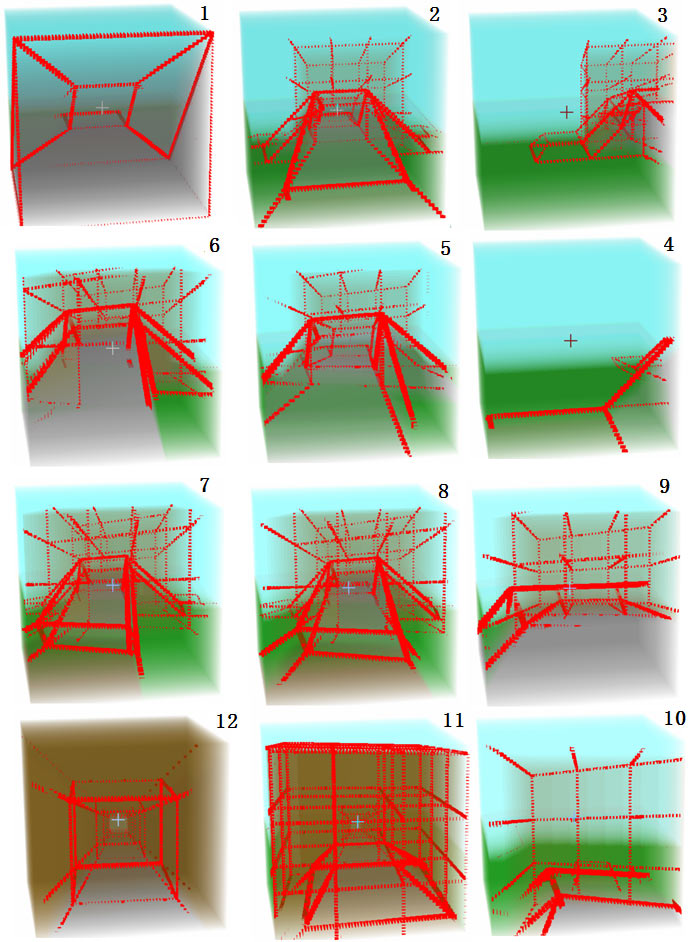
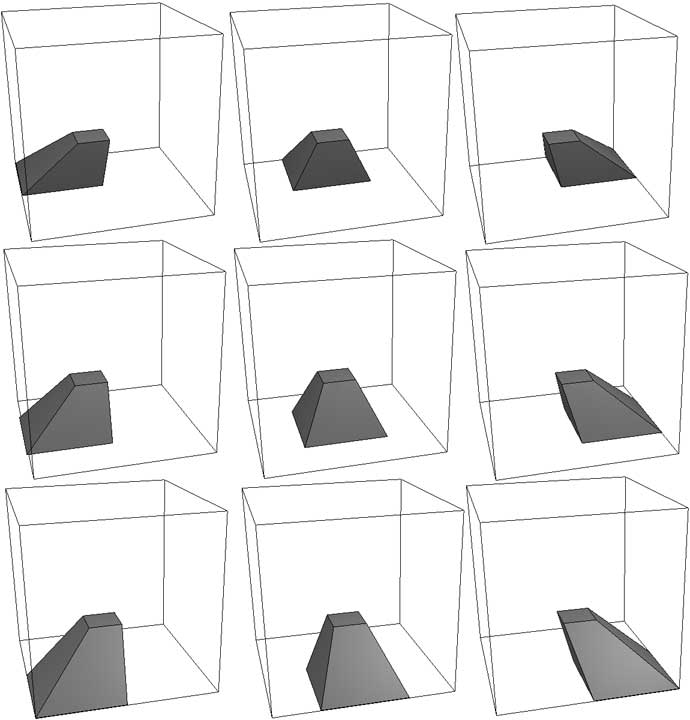
这里我着重说一下怎样才算把棱台对齐了,请看下图。下图中只有中间的棱台是对齐的,如果偏左,说明你往路的右边偏离,反之亦然。注意左右方与侧前侧后方本质都是一种侧面方向,如果视野不是立方体(比如圆柱或球形),四维人没有外在参照物来区分左右方与侧前侧后方(只能用它们身体器官的位置)所以左右方要注意对齐那么侧前侧后也同样需要。如果你觉得很不适应看侧前侧后方向可以按Z X键让视图旋转,这种旋转会交换左右方与侧前侧后方,但保持前进方向与竖直方向不变(这就是我们在讲四维车时说到的那种自转!)。
你能在天黑之前完成挑战吗?(第一次接触四维星球的太阳与昼夜循环?没你想象的简单!请看这篇文章)
地图俯视图与水平截面
如果你对只看3D视野中的线框走路感兴趣的话,推荐你玩这个Java小程序:4DBlocks,这是一个基于3D视野仅线框显示的四维迷宫、四维场景显示器。我之前在这里也安利过它,它也是现在这个4DViewer的灵感来源。
在那个四维迷宫里特别容易迷路,我每次都是瞎走到终点的(因为迷宫规模特意设置得很小,你想挑战可以改大)如果这个迷宫是纯三维的,也就是说能够放在四维世界的三维地面上,那么如果能直接看到三维地图肯定就比直接在迷宫里走简单多了。怎样得到地图呢?联想现实中的地图,早期是通过测绘得到的,现在都是卫星直接高空拍摄了。所以我们也可以直接按空格键飞上天,再滚动鼠标滚轮俯视大地就行了。还是以刚才那个上坡钻隧道的场景为例:到一定高度后俯视大地,此时你的立体视野的背景应该都是大地的绿色,然后你看到了下面的东西:虽然隐约能看到5个坡道和一条往隧道走的路,但模糊得很。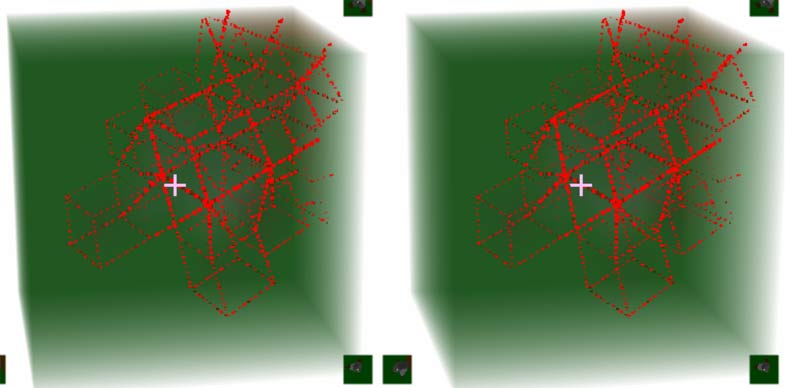
你可以按C打开线框提高分辨率,用Z X旋转视图慢慢看,但有没有像截面那样更清晰的三维地图呢?有!让我们落回到地面上,滚动滚轮将俯仰角调至水平。注意看你的右上方水平截面。我们先在坡底别上坡。之前说过,晃动鼠标的感觉就是在水平截面中上下左右张望。现在请只看右上截面,忽略其它视图,想象你像开飞机一样,直接用鼠标控制方向,用W键前进。由于只有一定高度坡度的物体才会与水平截面相交,所以你看到的正是坡道与平台的立体地图形状!现在你可以对准一个坡道上坡(只看水平截面并不能知道是坡道还是墙,所以也要偶尔看看其他视图哦)你会发现水平截面中所有东西都消失了,只有天空的颜色。那是因为你的海拔上升,截面不再与路面相交了。转动鼠标滚轮低头看才能重新看见道路。所以右上放水平截面给了我们看特定高度的3D截胞的便利。当然严格来说这也不算地图(因为还是第一人称视角)。
进一步体验四维世界
好了,今天的四维世界之旅就告一段落了。如果你还没玩够,或觉得这些场景还不够有意思,在这里你能发现更多的4D场景、游戏(包括4D版Minecraf!)、刚体物理场景(教程看这里)!