我在以前的四维空间系列文章中描绘了一个四维星球上的世界。这次要研究的是四维星球自转公转产生的昼夜和季节变化。我们假设这个星球近似为超球,那么第一件要做的事就是怎样描述超球上的一点,这难不倒我们,因为类似球坐标系,我们可以用超球坐标系构造出类似经纬度的表示方法,只是超球表面是三维的,要三个度数表示。
在说这个星球的旋转之前我先简单介绍一下四维空间中物体的旋转:它和三维空间最大的不同就是有“双旋转”。旋转其实是一种二维空间独有的效应:转动平面xy,除了原点外的所点的轨迹都是xy上面的圆。在三维空间中转动平面xy,空间中点的轨迹在xy面上的投影也是一个圆,但注意z轴上的点都没有动,这就是旋转轴。四维空间中转动平面xy,空间中点的轨迹在xy面上的投影也是一个圆,但注意zw坐标面上的点都没有动,所以我们说四维空间旋转是绕着面转动的,你发现问题了没有?其实发生旋转的坐标都只是x、y,但我们却关心的是没参与旋转的部分,这才导致了旋转轴、平面等有不一致的维度。其实四维空间存在除了原点都在动的“双旋转”,这使得我们必须放弃关心没参与旋转的部分:如果一个旋转是xy面和zw面上同时旋转的结合,这就叫双旋转——这是可能的,因为两个平面是绝对垂直的,两个方向上的运动没有干扰,旋转速度也可以不一样。可以证明,四维空间中所有旋转要么是有不动旋转面的简单旋转,要么是除原点外所有点都在运动的双旋转,而每个双旋转又可以分解成两个绝对垂直的单旋转的复合。Hadroncfy的这篇文章详细介绍了双旋转中点的运动。
回到星球的自转上来:我们的宇宙中由于形成初期一些复杂的原因,星球或多或少都在自转,对于四维星球来说双旋转就是一种最一般的自转状态。我们将双旋转分解成两个绝对垂直的单旋转的复合,这两个旋转的速度不一定相等,我们把速度大的旋转平面定为xy平面(下图中红色圆),速度小的平面定为zw平面(下图中红色线,其实也是圆,由于球极投影过极点$-w$),这样就可以建立一个四维直角坐标系。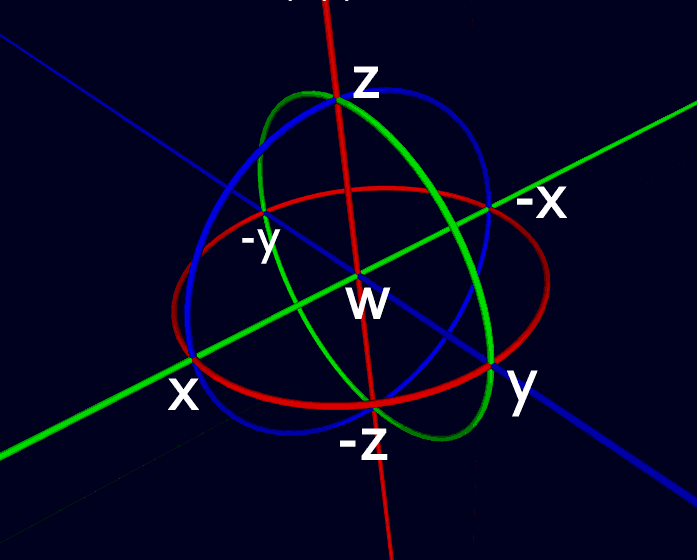 注意球极投影展示的是超球表面,标出的坐标点是坐标轴与超球表面的交点,坐标原点在球心处,是在球极投影中表示不出来的。
注意球极投影展示的是超球表面,标出的坐标点是坐标轴与超球表面的交点,坐标原点在球心处,是在球极投影中表示不出来的。
下面问题就来了:既然星球没有自转轴,怎样规定南北极?很简单,我们人为规定一个就是了,比如选某个天文台做北极点?但定个经度0°点还凑合,这样完全“钦定”极点就有点过分了。我们还有个选择就是放弃超球坐标系,使用超球上另一套Hopf坐标系来描述地点,它可以自然地与双旋转星球适配。
| 超球坐标:$$\begin{aligned} x&=r\cos \psi \\y&=r\sin \psi \cos \theta \\z&=r\sin \psi \sin \theta \cos \varphi \\w&=r\sin \psi \sin \theta \sin \varphi \end{aligned}$$ | Hopf坐标:$$\begin{aligned}x&=\cos \xi _{1}\sin \eta \\y&=\sin \xi _{1}\sin \eta \\z&=\cos \xi _{2}\cos \eta \\w&=\sin \xi _{2}\cos \eta .\end{aligned}$$ |
- 在三维世界中,星球拥有赤道。对星球上每个点(除了极点)来说,星球转动的方向叫东,相反的方向叫西。
- 在四维世界中,我们不去找2维的球形赤道,相反我们把相互垂直的旋转平面与星球表面的交线(两个红色圆周)作为赤道。这样我们得到了两个赤道——xy面上的圆和zw面上的圆。xy面转得快一些,我们叫它快道,zw面转得慢一些,我们叫它慢道。对星球上每个点来说,xy面转动的方向叫东,相反的方向叫西,zw面转动的方向,没名字,我叫它阴,相反的方向叫阳,这是四维空间一组新的方位词,你不满意可以换叫法。(英语中有人叫Marp和Garp)阴阳与东西方向是垂直的。
现在三维的超球表面还剩一个方向(与前面两方向都垂直)没定义了,它就是南北方向:只要没在两个赤道上的点,北就是指向zw面上的赤道圆上最近的点的方向(下图中R),南就是指向xy面上的赤道圆上最近的点的方向(下图中Q),它们互为反方向,与东西、阴阳垂直。注意这样南极不再是点,而是xy面的快道,北极便是zw面的慢道。以后我们将以南极、北极来称呼这两个垂直的圆周(图中红色两圆)。
那么现在星球上的经纬线是什么样子的?答案是:它已经在《维度数学漫步》影片中部分出现过了。还记得一个球极投影是拥有四簇圆的圆环面吗?它就是超球上的一张等纬度面(纬面),圆环上的经纬线就是东西与阴阳方向。 我们习惯把南极xy面的快道作为0°,北极zw面的慢道为90°。南北方向只有90°而不是像地球一样南北纬一共180°!这是Hopf坐标(对应前面公式里的$\eta$)比较奇怪的地方。不过也好理解,xy面与zw面是绝对垂直的,南北方向的纬度就是表示离两个平面的远近的,所以范围在0~90°之间。经度怎么办?由于四维星球和地球一样,旋转方向圆周上任意一点地位都一样,我们还是不得不人为规定0°东西经面和0°阴阳经面。这些经度类似地球上的经度取值0~360°(对应前面公式里的$\xi_1$和$\xi_2$),它们是一些半球面,好比地球上的经线是半圆。
我们习惯把南极xy面的快道作为0°,北极zw面的慢道为90°。南北方向只有90°而不是像地球一样南北纬一共180°!这是Hopf坐标(对应前面公式里的$\eta$)比较奇怪的地方。不过也好理解,xy面与zw面是绝对垂直的,南北方向的纬度就是表示离两个平面的远近的,所以范围在0~90°之间。经度怎么办?由于四维星球和地球一样,旋转方向圆周上任意一点地位都一样,我们还是不得不人为规定0°东西经面和0°阴阳经面。这些经度类似地球上的经度取值0~360°(对应前面公式里的$\xi_1$和$\xi_2$),它们是一些半球面,好比地球上的经线是半圆。
下面来讨论星球上的日夜更替:我们假设和地球类似,太阳离星球很远,以致于阳光可以近似看成平行光。平行光将照亮半个超球,同时另一半将处于黑夜当中。此时地球上的晨昏交界线(圆周)对应到四维就升级成了晨昏交界面(球面),它把超球分成昼半超球和夜半超球两部分。昼夜更替随着星球的转动产生了,但是居住在南极和北极附近的人们感受到的昼夜更替完全不同:南极是xy较快速的旋转平面,一天较短,称为短日;北极是zw较慢速的旋转平面,一天较长,称为长日。而在中纬度地区同时受到两种速度旋转的影响,每天时间会忽短忽长,两种圆周运动相互合成,最终让太阳轨迹变得像李萨如图形那样变幻莫测,如果转速之比是无理数,则太阳轨迹永远没有封闭轨道,有点像三体里的乱纪元。(但这不是混沌现象,其实是完全能预测的)
注意,这颗星球还在绕太阳公转。牛顿定律告诉我们,它的稳定公转轨道必须是个正圆,所以我们不用担心考虑带双旋转的公转了。公转会导致季节变化,但这种季节模式和我们熟知的春夏秋冬又不一样。我们最关心的是太阳直射点的纬度,因为两个经度方向都是自转方向,可以被“抹匀”,昼夜更替情况是一样的(除了时差,我们后面再讨论),这跟地球上的情况也是相似的。
- 在太阳直射南极快道的时候,没有任何地方有长日交替。南极道上短日变化最明显,往北变化减弱,直到北极道整个都落在了晨昏交界面上,导致北极出现极晨极昏现象,这和春秋分地球上南北极的情况相似;
- 在太阳直射北极慢道的时候,没有任何地方有短日交替。北极道上长日变化最明显,往南变化减弱,直到南极道整个都落在了晨昏交界面上,导致南极出现极晨极昏现象;
太阳直射点如果在中纬度,每个地方都至少有一种昼夜交替,没有极晨极昏现象,更没有极昼极夜。但公转到底会让直射点怎样运动呢?在地球上这取决于黄赤交角——公转平面黄道与地球自转所在面赤道的夹角;在这个星球上也取决于黄赤交角,但四维空间中两平面需要两个夹角参数来描述位置关系,我们不妨设公转平面与南极道所在xy面夹角为$\theta_1$和$\theta_2$,则公转平面与北极道所在zw面夹角为$90°-\theta_1$和$90°-\theta_2$,角度互补是因为xy面与zw面绝对垂直。太阳直射点的纬度值其实就是阳光所在直线与南极道所在xy面夹的线面角。随着地球的自转,阳光所在直线的方向不断变化,这些方向都平行于公转黄道面。我们之前提过平面之间两个角度的含义就是取一个平面上所有的方向与另一个平面的线面角的最大值和最小值,这就说明太阳直射点只会在$\theta_1$和$\theta_2$的纬度范围内波动,周期为半年,这个范围内的点是热带,其余地方就是寒带了。我们把太阳直射在低纬度的时间叫短日季,直射在高纬度的时间叫长日季,之所以这样叫是有原因的。我写了个javascript小程序模拟了一下星球上不同位置的太阳高度角余弦值随时间变化的曲线,下图是黄道与极道二面垂直($\theta_1=0°$、$\theta_2=90°$,比如xz平面)的公转系统: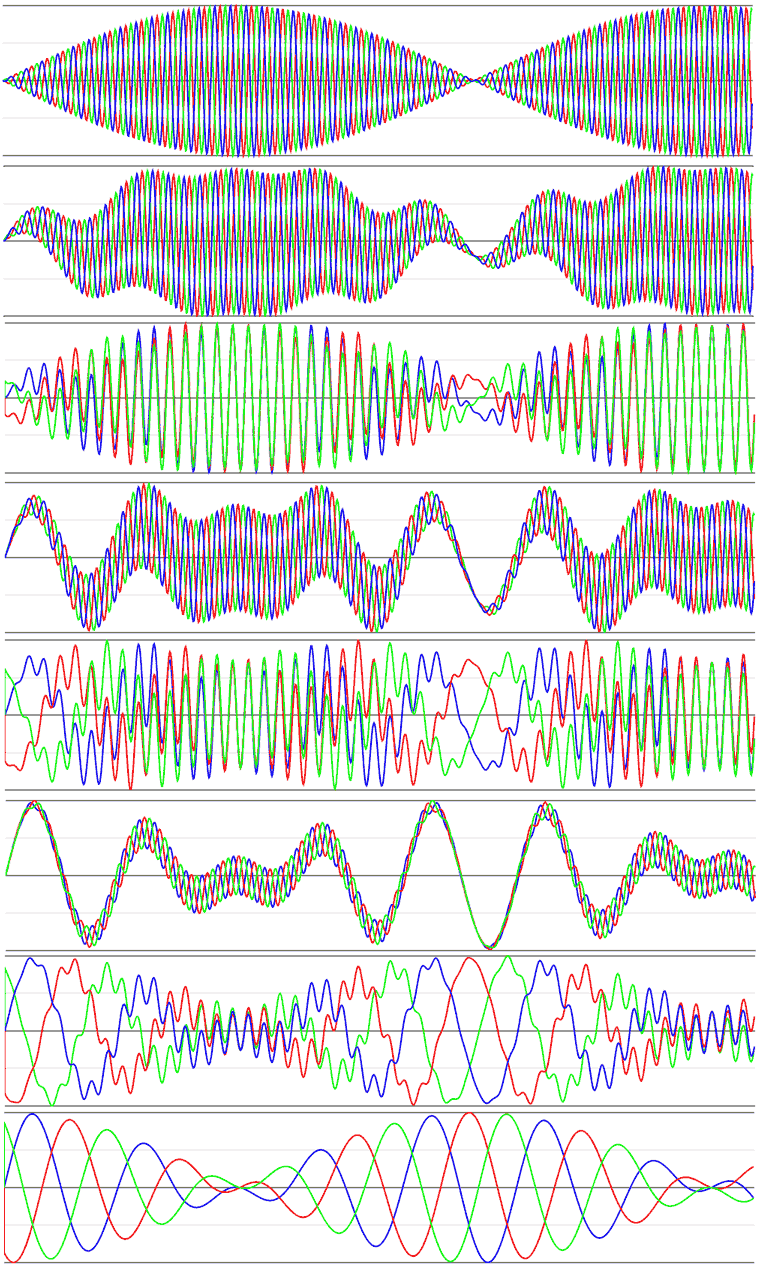
- 1:南极圈上东西经度相差120°的三个点(对应红绿蓝三条线):我们可以明显看到短日变化和时差。太阳直射南极时短日变化最明显,随着季节更替,太阳直射到北极,短日变化消失了,南极圈上产生了短暂的极晨极昏。
- 2:纬度15°同阴阳但东西经度相差120°的三个点:太阳直射南极时短日变化最明显,无长日变化,随着季节更替,太阳直射到北极,短日变化消失了,但长日变化明显了,此时这三个点处于长日的夜晚,不算极晨极昏。
- 3:纬度15°同东西但阴阳经度相差120°的三个点:我们看到它们的短日变化是一致的,没有时差,但太阳直射到北极短日变化快消失时,长日的时差表现了出来。
- 4、5:纬度45°地区:与纬度15°类似,只不过太阳直射南极时的短日变化比不上纬度15°的那么明显了,相反太阳直射北极时明显看到长日变化更大了。
- 6、7:纬度75°地区:短日变化很弱,长日变化占主导。
- 8:北极圈上阴阳经度相差120°的三个点:我们可以明显看到长日变化和时差。太阳直射北极时长日变化最明显,随着季节更替,太阳直射到南极,长日变化消失了,北极圈上产生了短暂的极晨极昏。
对于一般的公转系统,黄道与极道的两个夹角都在0°到90°之间,且不相等,这样任何地方任何时候都有至少一种昼夜变化。若黄道与极道的两个夹角相等(等角平面),则整个星球没有季节变化。
现在总结起来:短日、长日变化取不仅决于你所在地方的纬度,还取决于太阳直射点的纬度(季节),长短日变化是这两个因素双重作用的结果。这个星球上的人有必要使用两种日历系统:长时和短时,存在两种不同的时区划分。南北方的时间长短的差异导致人们的生物钟都不一样,只有中纬度的人才能适应所有地方的生活,因为中纬度地区是乱纪元,没有规律。下面我们讨论一下一种叫等角旋转的特殊双旋转:如果xy面与zw面转速一样,则短日、长日时间相同,更有趣的是,由于等角旋转的高度对称性,星球上每一点旋转的轨迹都是圆(这些圆将超球表面填满,构成Hopf纤维丛!两两圆周都等角!),这些圆的地位都相同,谁都可以充当南极道北极道!可惜自然界哪有那么精确的系统呢,更可能的情况是这两种旋转速度差不多,但就差那么一点,这足以打破上面的对称性让我们找到唯一的南极道北极道,因为在中纬度地区同时有长时和短时,这种微妙的速度差会逐渐累积,导致长时的白天晚上和短时的白天晚上错位,如果相位完全相反就会形成极晨极昏现象,而这种现象有周期性可能过几天又错回来了,和物理上的拍频原理相当。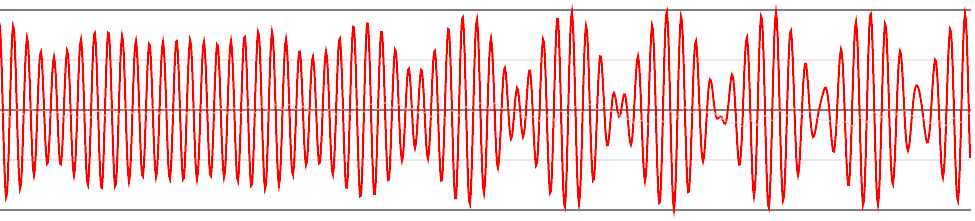 南北极地区永远没有拍频现象,太阳直射到南北极时也不会有拍频现象,所以这种现象比较极端。其实太阳是否落下都要短时、长时共同决定,而短时、长时所占的比重还要由纬度、季节决定,所以四维星球上文明的历法系统真的很复杂。
南北极地区永远没有拍频现象,太阳直射到南北极时也不会有拍频现象,所以这种现象比较极端。其实太阳是否落下都要短时、长时共同决定,而短时、长时所占的比重还要由纬度、季节决定,所以四维星球上文明的历法系统真的很复杂。
下面是Javascript计算太阳高度角的小程序:(适合电脑查看,我没写适合手机的布局)
下一步我们将了解星球上的磁场以及四维人的指南针,但由于磁场不再是向量,而是四维像旋转那样的平面量(简单2-向量),还有与双旋转类似的复杂2-向量,涉及的都是外代数、几何代数的知识,我们就先在这里打住了,以后我将写一篇文章(写好啦!点这里)专门介绍四维空间中的电磁学。
23年更新
跟上面提到的电磁场一起,我做了个交互式的四维星球场景,你可以动态观察这颗星球上的太阳运行规律,还可以用指南针进行导航:
该星球的参数如下:
- 长日为短日的2.87倍;
- 星球公转周期为100个短日;
- 星球的黄赤交角为12度与43度。
