四维空间(七):N维的向量
# 本系列文讨论的是纯空间上的几何,但本文将要涉及的k-向量的某些性质在四维时空中也成立(只是度规不一样)。本文对数学能力要求较高:将出现大量数学公式。k-向量在除相对论(时空)以外的物理上也有用武之地,详见CFY的文章角速度、轴矢量、2-矢量从另一个角度——物理学引入k-向量。
该谈谈定量的四维空间计算问题了。它一方面可以检验我们几何直觉的正确性,不然我们的直觉只是在瞎猜而无证据;另一方面在编程计算四维图形中离不开计算。
向量不再适应四维几何
大家应该都知道n维向量点乘叉乘算夹角算法向量。点乘早就拓展到了N维,所以计算线线角没问题,三维空间遇到平面我们就用它的法向量来参与夹角运算——因为平面的法向量方向是唯一的;四维空间中的三维胞我们也用它的法向量来运算——因为它的法向量方向也唯一的。但问题是:平面的法向量不唯一——因为四维空间中,平面的法空间也是二维的,即法平面也是平面。这样永远也转换不到向量求解!
当然平面也写得出解析式:两胞方程联立的交面式,但太麻烦了——你做立体几何难道喜欢交面式方程表示直线吗?
平面是能用向量表示的:$\vec x=\lambda\vec m+\mu\vec n {,}\lambda,\mu\in \mathbf R$,但这里的向量和参数的选择都有任意性,参与运算也不方便。我们只能从另一层面上突破:拓展叉乘到高维。
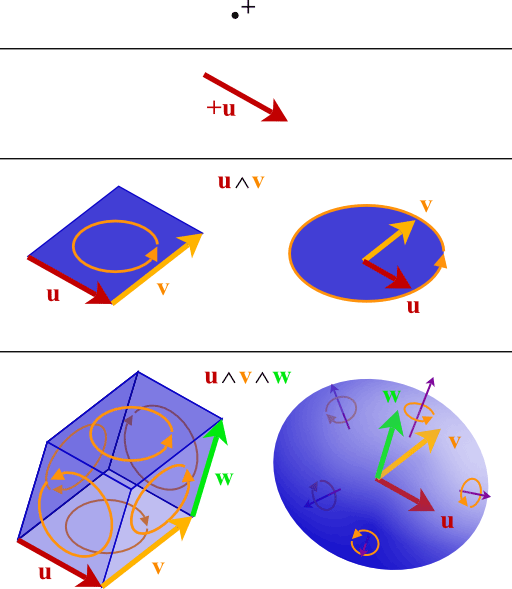
当然,我们还有一条路:直接用一个类似向量的量表示平面,并能和其他向量做内外积,从而方便地算投影、算夹角。这种新的量叫2-向量(二重向量)我们前面分析得到,2-向量表示平面,而平面由两个不共线普通的向量(1-向量)张成,所以我们规定一个两个1-向量间的运算“$\vec a\wedge\vec b$”,这个符号我们叫它楔形积(简称楔积)。
我们前面想推广外积(叉乘),所以我们又把外积搬过来,使两者结合一下:$\vec a\wedge\vec b$是一个有大小有方向取向的量:取向就是由$\vec a$、$\vec b$张成的平面,且遵循右手螺旋法则(意思是$\vec a\wedge\vec b=-\vec b\wedge\vec a$),大小(范数)为由$\vec a$、$\vec b$张成平行四边形的面积,所以若$\vec a$、$\vec b$共线,则$\vec a\wedge\vec b=0$。这个想法很好,但现在还没用处,因为我们还要来看在坐标下具体怎么表示、计算。
楔积与2-向量
三维情形
这是我们三维空间都没用过的数学工具。所以我们先在三维空间中讨论、熟悉它,再推广到四维至N维。设$\vec m=(x_1,y_1,z_1),\vec n=(x_2,y_2,z_2)$ ,则$\vec m\wedge\vec n=(x_1\vec e_x+y_1\vec e_y+z_1\vec e_z)$ $\wedge(x_2\vec e_x+y_2\vec e_y+z_2\vec e_z)$.
怎么打开括号?如果$\wedge$满足分配率括号就能打开了!我们不妨先假设它满足吧,展开,并利用$\vec a\wedge\vec b=-\vec a\wedge\vec b$化简合并(我们还得假设它是线性算子才能合并)得:$$\vec m\wedge\vec n=(x_1y_2-x_2y_1)e_x\wedge e_y + (x_1z_2-x_2z_1)e_x\wedge e_z + (y_1z_2-z_2y_1)e_y\wedge e_z$$
眼熟吧,这就是我们熟知的叉乘公式。我们把叉乘搬给了“$\wedge$”运算,所以推出叉乘公式很正常。这个2-向量有三个独立分量$e_x\wedge e_y、e_y\wedge e_z、e_x\wedge e_z$,它们表示单位$xy、yz、xz$平面,刚好对应法向量$\vec e_z、\vec e_x、-\vec e_y$(注意这种对应都遵从右手定则,有时会差一个符号),给人感觉它们是同构(相同)的。但$\vec a\wedge\vec b$与$\vec a \times \vec b$有本质区别:前者代表平面,后者代表平面的法线,我们只是找到了一种特殊的对应它们的关系:$$a(e_x\wedge e_y)+b(e_y\wedge e_z)+c(e_x\wedge e_z)\to a\vec e_z+b\vec e_x+c\vec e_y$$这种对应我们叫霍奇对偶,后面会大量用到。
四维情形
而四维空间直线和平面(2-向量)不再有一一对应的关系了:
设$\vec m=(x_1,y_1,z_1,w_1),\vec n=(x_2,y_2,z_2,w_2)$ ,则$$\begin{align} \vec m\wedge\vec n&=(x_1\vec e_x+y_1\vec e_y+z_1\vec e_z+w_1\vec e_w)\wedge(x_2\vec e_x+y_2\vec e_y+z_2\vec e_z+w_2\vec e_w) \\ &=(x_1y_2-x_2y_1)e_x\wedge e_y+(x_1z_2-x_2z_1)e_x\wedge e_z+(x_1w_2-x_2w_1)e_x\wedge e_w+(y_1z_2-z_1y_2)e_y\wedge e_z+(y_1w_2-w_1y_2)e_y\wedge e_w+(z_1w_2-w_1z_2)e_z\wedge e_w\end{align}$$
我们看到四维空间2-向量有六个独立的分量,是各坐标的两两组合,分量大小是两坐标交叉相乘再相减。好了,总算能表示出平面了。
2-向量内积及意义
下一步规定2-向量之间的内积:最自然的定义是对应分量相乘再相加,即$$\begin{align} A&=a_1e_{xy}+b_1e_{xz}+c_1e_{xw}+d_1e_{yz}+e_1e_{yw}+f_1e_{zw} \\ B&=a_2e_{xy}+b_2e_{xz}+c_2e_{xw}+d_2e_{yz}+e_2e_{yw}+f_2e_{zw} \\ 则A\cdot B&=a_1a_2+b_1b_2+c_1c_2+d_1d_2+e_1e_2+f_1f_2 \end{align}$$
($e_{ij}$为$e_i\wedge e_j$的简略写法,下同)
我们不妨写出夹角公式:
$$\lvert \cos\langle A,B\rangle\rvert={\lvert A\cdot B\rvert\over \lVert A \rVert \lVert B \rVert}$$
这里的2-向量的范数(大小)当然是2-向量与自身的内积再开方。好像一切问题都解决了!但等等,还有点地方不对:这里只出现了一个角!我们前面还分析了半天平面之间要用两个角来表示。
比如我们先做下列简单的计算:
$e_{xy}$与$e_{xy}$、$e_{xy}$与$e_{xz}$、$e_{xy}$与$e_{zw}$角度分别为:0°、90°、90°。
嗯,$xy$平面自身的夹角余弦为肯定是0°,但后两者都是90°:我们求出来的这个角度有意义吗?它与衡量平面的那两个角有什么关系?
还记得上一篇文章最后射影面积定理的推广吗?我们大胆猜想:2-向量内积的本质是一个面量乘以另一个面量在它上面的投影,所以我们得到四维空间面量间的点乘的几何意义:
$$\lvert \cos\langle A,B\rangle_1\cos\langle A,B\rangle_2\rvert=\lvert \cos\theta_1\cos\theta_2\rvert={\lvert A\cdot B\rvert\over \lVert A \rVert \lVert B \rVert}$$
这个式子和射影面积定理的作用是一样的。一般情况下一个方程两个未知数是解出$\theta_1、\theta_2$的。没关系,至少我们得到了一种坐标解法,而射影面积定理是几何方法。
2-向量内积跟向量内积很相似,所以我们还能推出:只有两个二向量对应分量成比例($A=kB,k\in \mathbf R$)时,才有$\lvert \cos\theta_1\cos\theta_2\rvert=1$,即$\theta_1=\theta_2=0$。所以就像向量那样若两2-向量成比例“共线”,则它们代表同一张平面。其实反之也成立,我们先不证明。
叉乘推广
霍奇对偶
回想$\vec a \times \vec b$与$\vec a\wedge\vec b$之间的关系:它们相互垂直,互为正交补,且大小(范数)、分量都相同,但它们的几何维数、意义都不同。我们规定霍奇对偶映射:将一个k-向量映射成它的正交补$(N-k)$-向量。把$A$的霍奇对偶记作$*A$,这里N是空间维数,我们讨论的即N=4的情况。霍奇对偶还要求$(N-k)$-向量与k-向量的大小(范数)相同,且$(N-k)$-向量的方向遵循右手定则——我们无力用右手在高维空间比划,其实这是一个抽象的法则,我们用具体例子说明:
$*e_{xy}=e_{zw}$、$*e_{yz}=e_{wx}$、$*e_{zw}=e_{xy}$、$*e_{wx}=e_{yz}$
只要我们保证角标从左到右是xyzw yzwx zwxy wxyz这样轮换,等式就是成立的。否则任意交换顺序中两个字母的位置会反号。如$*e_{xy}=e_{zw}$,但$*e_{xz}=-e_{yw}$。在数学上这叫奇排列和偶排列。(和行列式的奇偶正负交错类似)
$$\begin{align}设F&=a_1e_{xy}+b_1e_{xz}+c_1e_{xw}+d_1e_{yz}+e_1e_{yw}+f_1e_{zw} \\ 则*F&=f_1e_{xy}-e_1e_{xz}+d_1e_{xw}+c_1e_{yz}-b_1e_{yw}+a_1e_{zw} \end{align}$$
2-向量外积
现在我们可以描述叉乘的实质了:m-向量和n-向量在N维空间中做叉乘,得到了一个(N-m-n)-向量:它是m-向量和n-向量张成的空间(一个(m+n)-向量)的正交补,方向遵循右手定则。(注:这只是向量叉乘的一种推广,仅在本小节使用,后面我们将用$\times$符号表示2-向量之间的另一种类似向量叉乘的叫混合积的运算)
比如2-向量$F\times G=*(F\wedge G)$。注意这里$F\wedge G$是个4-向量!这次我们还要假设运算$\wedge$有结合律,即$(A\wedge B)\wedge C=A\wedge (B\wedge C)$。
$$\begin{align} 设F&=a_1e_{xy}+b_1e_{xz}+c_1e_{xw}+d_1e_{yz}+e_1e_{yw}+f_1e_{zw} \\ G&=a_2e_{xy}+b_2e_{xz}+c_2e_{xw}+d_2e_{yz}+e_2e_{yw}+f_2e_{zw} \\ 合并&化简得到: \\ F\times G&= (a_1f_2-b_1e_2+c_1d_2+d_1c_2-e_1b_2+f_1a_2)e_{xyzw}\end{align}$$
$e_{xyzw}$的霍奇对偶是一个0-向量,即“标量”:“1”。此“标量”不是真正的标量,因为空间反射变换下会反号(右手定则在作怪),我们叫它伪(赝)标量。
注意:我们没有再规定2-向量$F\wedge G=-G\wedge F、F\wedge F=0$了。实际上$F\times G=G\times F$因为我们交换变量时角标从1234变成了3412,有偶数个发生了交换,负号被抵消了!所以我们又可以愉快地用交换律了。同样的结论有$**F=F$,但此结论对其他k-向量不一定成立。
最终我们得到:2-向量间叉乘也得到标量。我们发现它的形式很像两个向量的内积——都是一些相乘项相加,其实我们有:$F\times G=F\cdot (*G)=G\times F=G\cdot (*F)$。
几何意义
$A \times B$是个标量:它的绝对值等于它们张成平行八胞体(想想平行六面体)的超体积:两个平面怎么张成平行八胞体?如果$A=\vec a\wedge \vec b$,$B=\vec c\wedge \vec d $,则$A\wedge B=\vec a\wedge \vec b\wedge \vec c\wedge \vec d $——其实就是以这四个向量做出的平行八胞体。这个定义是良好的,因为若$\vec a_1\wedge\vec b_1=\vec a_2\wedge\vec b_2=A$,由$\vec a_1、\vec b_1、\vec c、\vec d$围成的平行八胞体与$\vec a_2、\vec b_2、\vec c、\vec d$围成的平行八胞体虽然形状不一样,但可以证明它们体积是相同的。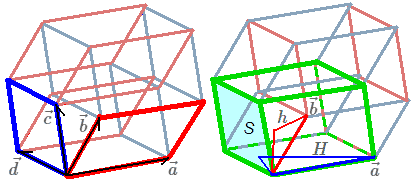
为了方便,我们先选一组特殊的$\vec a\wedge \vec b=A$:其中$\vec a、\vec b$为平行于两平面间最大角和最小角方向的向量(它们与$B$夹角为$\theta_1、\theta_2$)。平行八胞体四维体积$V_4=V_3h$。$V_3$指平行八胞体中任意一个平行六面体胞(如图中绿色)的三维体积,$h$为这个胞在平行八胞体中所对应的高。而$V_3=SH$。由几何关系:$h=\lVert\vec a\rVert \sin\theta_1$、$H=\lVert\vec b\rVert \sin\theta_2$得:$V_4=S\lVert\vec a\rVert\lVert\vec b\rVert \sin\theta_1 \sin\theta_2=\lVert A \rVert \lVert B \rVert \sin\theta_1 \sin\theta_2$
问题完美解决!
$$\lvert \cos\theta_1\cos\theta_2\rvert={\lvert A\cdot B\rvert \over \lVert A \rVert \lVert B \rVert} $$$$ \lvert \sin\theta_1\sin\theta_2\rvert={\lvert A\times B\rvert\over \lVert A \rVert \lVert B \rVert}$$
两个方程两个未知数,我们求得出两个角度了!N-维空间的所有角度问题是不是都能这样做呢?遗憾的是这种方法只在四、五维有效——六维时,两个胞需要三个角度参数才够描述,但内外积只有两个方程,所以老实用线性代数吧。
幸好我们暂不关心高维。再回到四维问题上:给出向量$\vec m$与2-向量$A$,它们之间的夹角(线面角)怎么算?我们希望前面的公式继续成立。但内积是对应项相乘,四维空间中向量有4个分量,2-向量却有6个分量,我们无法计算内积。所以只好用外积了——还是先算:$\vec m\wedge A$,我们化简得到了一个3-向量:$ ae_{xyz}+be_{yzw}+ce_{zwx}+de_{wxy}$,通过霍奇对偶映射到向量$ae_w+be_x+ce_y+de_z$。显然,它的大小(范数)代表$m$与$A$组成平行六面体体积,方向为此平行六面体所在胞的法向——就像混合积一样,它几何意义很明确:
$$\lvert \sin\theta\rvert={\lVert\vec m\times A\rVert\over \lVert \vec m \rVert \lVert A \rVert}$$
由于线面角只有一个角度要求,我们不需要再用内积了。现在我们有了看起来强有力的计算工具了,但这些结论对不对呢?大家可以自行用2-向量法求超立方体中的线面角、面面角等问题与用几何法得到的结果来比较一下。我验算了很多,这两种方法得到的结果都是一样。
乌云
前面都是几何走在代数前面,现在我们试着反过来想一些问题:
- 四维空间不直观,这些推出来的东西没有严格证明,正确性不能保证;
- 2-向量的“方向”概念模糊;
- 向量相加有直观意义:平行四边形的对角线;那2-向量相加后对应的平面有没有几何解释呢?如$e_{xy}+e_{zw}代表什么平面?e_{xy}+e_{xz}+e_{xw}呢?$
下面一条一条回答:
- 首先第一条证明不是问题:我们可以先抽象地定义一个满足一定性质的线性算子$\wedge$,再反过来说明它与平面之间有一一对应的关系,然后用线性代数证明后面的一切。
- 计算$A=\vec a\wedge\vec b$时,我们可以在A平面上标出一个从$\vec a$绕向$\vec b$的漩涡:这个漩涡就是一种“方向”。我们来看看$A\times B$和$A\cdot B$的符号:改变一个面的方向(如$A\to -A$)内外积同时反号,故只要给定了两平面,无论我们选了什么2-向量表示它们,它们内外积乘积的符号是确定的。这反映了四维空间两个平面组成的图形是有“手性”(向左右手那样无法旋转重合)的!这就是对四维空间手性定量描述的一个方法。
- 我们先求出平行于平面$e_{xy}+e_{zw}$的向量$m(x,y,z,w)$:解方程$\vec m\times (e_{xy}+e_{zw})=0$即可:
$$\begin{align}(xe_x+ye_y+ze_z+we_w)\wedge(e_{xy}+e_{zw})&=0 \\ (ze_z+we_w)\wedge e_{xy}+(xe_x+ye_y)e_{zw}&=0 \\ ze_{zxy}+we_{wxy}+xe_{xzw}+ye_{yzw}&=0 \\ 霍奇对偶得:ye_x-xe_y+we_z-ze_w&=0\end{align}$$注意这是一个向量方程,即要求左边是零向量,那么问题来了——我们得到唯一解$\vec m=\vec 0$!没有直线与面$e_{xy}+e_{zw}$平行?别慌,我们再来看看其它直线和它的夹角:$$\begin{align}\lvert \sin\theta\rvert &={\lVert\vec m\times A\rVert\over \lVert \vec m \rVert \lVert A \rVert} \\ &={\sqrt{y^2+(-x)^2+w^2+(-z)^2}\over\sqrt{x^2+y^2+z^2+w^2}\sqrt 2} \\ &={\sqrt 2\over 2} \end{align}$$这里$m$是任意的一个向量,它与面$e_{xy}+e_{zw}$夹角都是45°!面$e_{xy}+e_{zw}$到底怎么了?
那$e_{xy}+e_{xz}+e_{xw}$情况如何呢?我们同样列方程,化简得到:$(z-w)e_y+(w-y)e_z+(z-y)e_w=0$:令这些系数为0,得$y=z=w$,$x$取值无限制。这个平面看上去倒正常。我们这样理解共胞平面的加法运算:垂直于它们交线的向量做正常的向量加法运算,再与它们的交线张成平面。下图蓝色就是所有面的交线,可以看到垂直于交线的红色向量做加法得到绿色向量,最终张成了黄色平面:$e_{xy}+e_{xz}+e_{xw}$。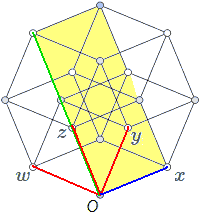
奇异(复合)2-向量
异胞怎么办?我们知道向量自身的叉乘为0,但$(e_{xy}+e_{zw})\wedge(e_{xy}+e_{zw})=2e_{xyzw}$,结果为2!所以我们只能认为根本不存在这样的平面与之对应!我们来看一般情况:$设F=ae_{xy}+be_{xz}+ce_{xw}+de_{yz}+ee_{yw}+fe_{zw},F\wedge F=2(af-be+cd)e_{xyzw}$。可以证明,只要满足$F\wedge F=0$的2-向量都是可以表示平面的,换句话即一定存在$\vec a、\vec b$,使$\vec a\wedge \vec b =F$。不满足$F\wedge F=0$的2-向量不对应平面!也不能写成$F=\vec a\wedge \vec b$
我们说满足$F\wedge F=0$(即能写成两向量”$\wedge$”形式)的2-向量是简单的,反之叫奇异或复合的。比如2-向量$e_{xy}+e_{zw}$就是复合的。向量(1-向量)可没这些情况,所以我们说向量(1-向量)都是简单的。
复合2-向量看起来是没用的。但2-向量不仅描述平面,还可以描述旋转。我们前面看到四维空间有简单旋转对应简单2-向量,三维没有的双旋转对应复合2-向量!
复合2-向量无非是普通2-向量通过加法得到的,所以我们要把它肢解成简单2-向量。
对偶分解
我们看2-向量$F=e_{xy}+e_{zw}$的霍奇对偶:$*F=*(e_{xy}+e_{zw})=e_{zw}+e_{xy}=F$它自己和自己对偶!再如$G=e_{xy}-e_{zw}$可以验证它是反自对偶:$G=-*G$。其实任意2-向量$A$都能分解成自对偶和反自对偶2-向量之和:$A={A+*A\over 2}+{A-*A\over 2}$。其中${A+*A\over 2}$是$A$的自对偶部分,我们以后为了方便记作$A^+$,${A-*A\over 2}$是反自对偶部分,记作$A^-$。(由霍奇对偶的线性和结论$**A=A$不难验证)
例如$A=e_{xy}$,分解得${(e_{xy}+e_{zw})/ 2}+{(e_{xy}-e_{zw})/ 2}$
这样我们有了一套新的基底表示2-向量:
自对偶三个分量:${\sqrt 2\over 2}(e_{xy}+e_{zw})、{\sqrt 2\over 2}(e_{xz}-e_{yw})、{\sqrt 2\over 2}(e_{xw}-e_{yz})$;
反自对偶三个分量:${\sqrt 2\over 2}(e_{xy}-e_{zw})、{\sqrt 2\over 2}(e_{xz}+e_{yw})、{\sqrt 2\over 2}(e_{xw}+e_{yz})$;
可以证明它们正交——两两内积为0——其实它们两两外积也为0!系数${\sqrt 2\over 2}$起归一化作用,保证它们为单位2-向量。
自对偶、反自对偶2-向量对应左、右手等角双旋转,所以我也把这个分解叫做“等角分解”。
正交分解
复合2-向量$A$一定能分解成表示两个绝对垂直的平面的2-向量之和。如果这个复合2-向量不是自对偶或反自对偶的,那么分解方式唯一:
$$A=({A^+\over\lVert A^+\rVert}+{A^-\over\lVert A^-\rVert}){\lVert A^+\rVert+\lVert A^-\rVert\over 2} + ({A^+\over\lVert A^+\rVert}-{A^-\over\lVert A^-\rVert}){\lVert A^+\rVert-\lVert A^-\rVert\over 2}$$
如果这个复合2-向量自对偶,则分解为:
$A=({A^+\over 2}+I^-) + ({A^+\over 2}-I^-)$,其中$I^-$可以是任意一个范数为${\lVert A^-\rVert\over 2}$的反自对偶2-向量。
如果这个复合2-向量反自对偶,则分解为:
$A=({A^-\over 2}+I^+) + ({A^-\over 2}-I^+)$,其中$I^+$可以是任意一个范数为${\lVert A^+\rVert\over 2}$的自对偶2-向量。
大家可以自行验证。正交分解的意义显著:一个双旋转可以看成两个绝对垂直的简单旋转的叠加!且若一个双旋转是等角的(即在两个绝对垂直平面上旋转速度相同),它能由任意与它等角的两个绝对垂直的简单旋转来合成。
与旋转矩阵的关系:生成元
下面我们要来看一下2-向量具体怎么表示旋转的。(以下资料均出自英文维基百科“四维欧几里得空间中的旋转”词条)物理上一般常用矩阵或张量形式表示2-向量。先介绍2-向量的矩阵形式:把$F=a\wedge b$写成 $F=ba^T-ab^T$(这里$a、b$是列向量),则我们得到反对称矩阵:$$F=\begin{pmatrix} 0 & F_{xy} & F_{xz} & F_{xw} \\ -F_{xy} & 0 & F_{yz} & F_{yw} \\ -F_{xz} & -F_{yz} & 0 & F_{zw} \\ -F_{xw} & -F_{yw} & F_{zw} & 0 \end{pmatrix}$$
我们知道四维空间中的旋转变换在代数上只不过是行列式为1的正交矩阵$M$,而我们的二向量$F$就是正交矩阵的生成元!先把2-向量单位化,再计算神奇的矩阵指数运算$M=e^{F\theta}$,其中$\theta$是标量:旋转角度。具体算法见wikipedia矩阵指数(Matrix exponential)中“Rotation case”一节。有了这个算法,我们用在四维空间中2-向量表示旋转就像用四元数表示三维旋转那么方便。(四元数也能表示四维空间中旋转,详情见这里)有了这些知识,写一个Jenn3d那样的鼠标控制在四维空间中滚动就没问题了。
更多2-向量的内容可参看维基百科:外代数。