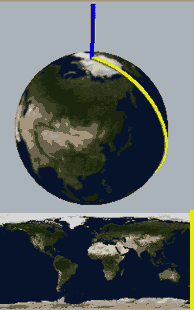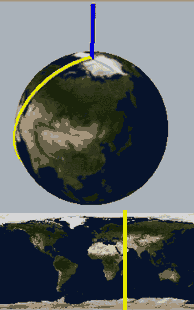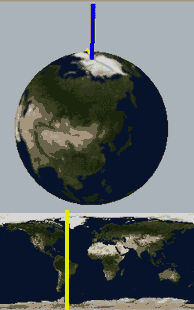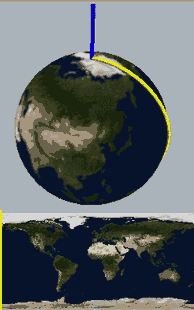
四维空间(十二):解开球面结
# 本文是《四维空间(十):扭结与环扣》的续集,本内容对空间想象力要求较高,可能有些地方难以理解,但全文没有任何公式,只涉及几何,不涉及代数,适合挑战空间想象力哦。
# 我发现不仅是我,网上“扭结”与“纽结”全都在混用,那我也懒得改了。
在本系列的上上篇文章中我们知道了四维空间中的二维曲面打结现象与各式各样的孔、环扣等,上次对二维曲面结的介绍其实也不算太详细,只给出了一些非平凡的管状结作为例子,今天我们要从另一个角度来分析扭结。本文的主要内容来自于这个Youtube视频与这篇论文,它介绍了通过旋转三叶结的方式来构造同胚于球面的结(即允许自相交的话能把这个结恢复成球面),并且证明了有些是真正无法解开的结,另一些是能够通过一些步骤解开成球面,下面我们也来试试解一解高维空间当中的结!
纽结旋转体
其实我们已经在上一篇文章中讲到过利用旋转来制造非平凡扭结。我们来复习一下:
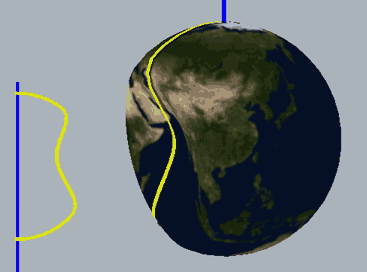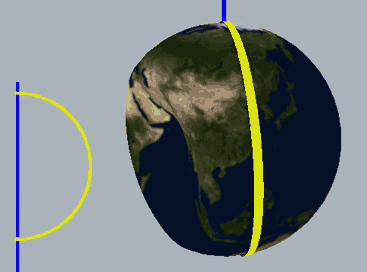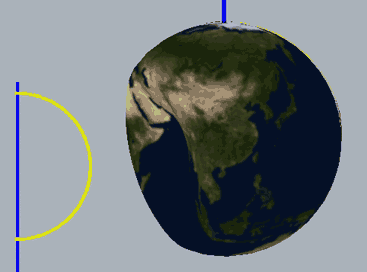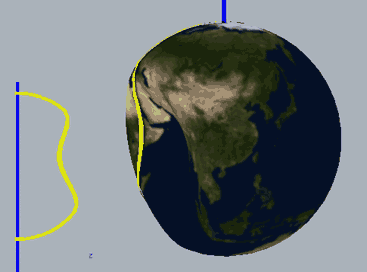
半圆旋转一周能得到球面,在半圆上打一个死结在四维空间中旋转一周能得到一种打了结的球面,注意在三维空间旋转中会得到自相交的曲面。那篇文章还提到,如果把旋转扭结叫公转,那么扭结在公转过程中还可以自转,得到一些更复杂的有额外“自转”的更复杂的扭结,这篇文章正是要做这样一件事:
三维扭结投影上的交点
按照我们的传统惯例,先研究一下三维空间中的结。比如以下是一个三叶结(最简单的死结)。如何向二维生物描述它呢?三叶结在拓扑上的本质是一个圆周(其实所有三维空间中的结都是!),我们找到一个点O直接将圆周剪开,(但注意拓扑学中不允许直接剪开物体,所以我们必须要能随时把两端粘回去),从点O出发,我们将经过投影的三个交点,为了尽可能保留一些信息,我们注明哪些交点对应哪些交点,并记录下每次经过交点是走的上面还是下面(从上面走就把字母写在线上方,下面走就写下方),最终得到下图右边这样一根线:
下面我给出一根线,你能复原出原本纽结的投影图吗?
先思考一下吧。。
复原方法很简单,我们画一条线,在上面标上对应的交点,如果遇到之前标注过的点,就将线从那个交点处穿过去,继续重复上述过程,直到走完一圈。我们发现除了第一次遇到之前标注过的点时可以有从左边穿过与从右边穿过这两种拓扑不等价的画法,其余的连接方式一定是固定的,这被Alexender证明了。注意投影的角度有很多,以上讨论都是在任意一个特定的投影上进行的。
现在我告诉你,上面的那个纽结可以被解开成一个圆周,你肯定不会惊讶,因为这很显然,但你现在要说服我们来自二维世界的朋友,你可以给他解释纽结投影的合法变形移动(Reidemeister移动),从而一步一步严谨地将上面的那个纽结解开,但他看到这些二维空间中复杂的自相交,感到很头痛(他视觉是一维的),这怎么办?我们可以让他只理解圆周上的那些交点发生的事就可以了,具体做法是,我们把每一种合法移动对应到圆周展开图上的一些交点的变动!(对!我们到时也用这种方法的升维版来处理球面结)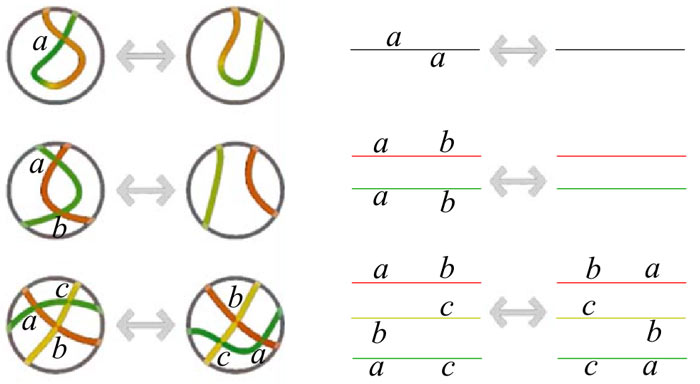
注意,这种方法只能证明两个结可以通过合法移动变得等价,但不能证明两个结不等价,幸好我们后面只是展开一个球面结证明它与球面等价。
或许你觉得这些线上的字母太抽象了,那么我们把时间轴作为另一根轴,这样就能把移动中交点的变化过程画出来。注意点动成线,所以原先的交点变成了一条轨迹,我们此时用红色代表从上面经过的交点轨迹,用蓝色代表从下面经过的交点轨迹,注意第三种合法移动涉及到三条线,因此就有并列的三张时间轨迹图:
注意这三种移动的中间位置都有一种“不好的”临界位置(比如第一幅图中投影有个尖点,两个交点在此处对消),一般我们会避免在纽结投影中出现,但移动时,这些状态是不可避免会出现的。
或许你已经注意到了,如果我们把时间轴看成空间,这些图形就是一些四维空间中二维纽结的交痕。但在正式讨论二维纽结的交痕前我们先来可视化一下我们的主角——旋转球面结。
新的四维图形可视化方法
我们得先知道“自转为360度的旋转球面扭结”是个啥东西,再说去解开它。本来就是抽象的四维空间,然后又有公转、自转,还要做形变,我们面对的是一个看似不可能完成的任务,但把这个任务一点点肢解后,我们将发现这也不太困难。首先我要介绍一种新的可视化四维图形的方法,它是一种截面法。但与以往的让四维物体从一个方向穿过三维面不同,这里用的是更适合于旋转体的旋转截面法:如果一个图形是完美的旋转体,则它的截面在不同角度都是一样的,但对于非旋转体来说,从不同角度截取得到的截面就不一定一样了。所以我们固定旋转面,通过旋转一周观察、描述旋转面上的图形的变化来观察、描述这个四维物体。这种方法其实也就相当于极坐标中沿着旋转方向的截面法。为了更好理解,我们只考虑三维空间中的二维球面的截线动画:我们把球面像世界地图那样展开成长方形,这时球面上的旋转截线(一些大半圆周)也跟着变成了世界地图上经度方向上的普通截线了。如果这个球体有一侧是瘪的,我们的旋转截线动画能够精确反映出这些形变。
|
|
|
我们知道,超球面可以由二维半球面绕平面旋转得到(对于能看到这的读者这应该是显然的吧),比如大家应该能够理解下面的旋转截面动画描述的是一个一侧凹一侧凸的超球面的旋转截面动画:
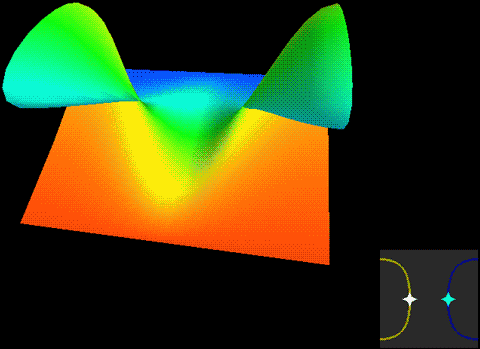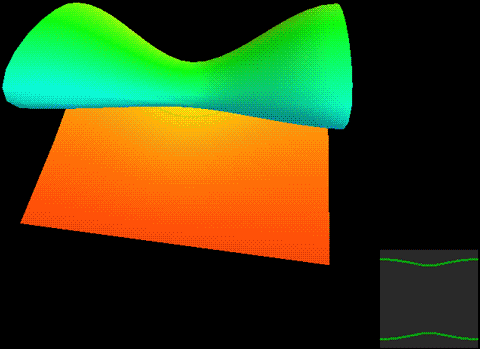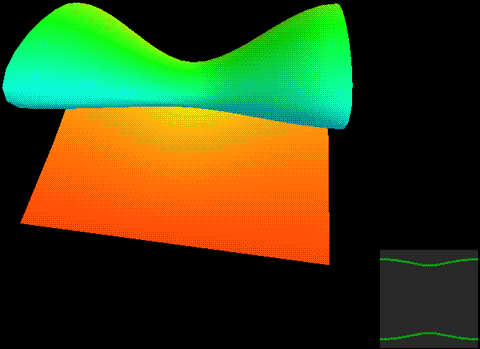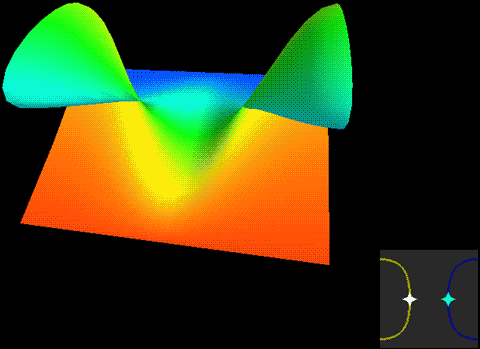
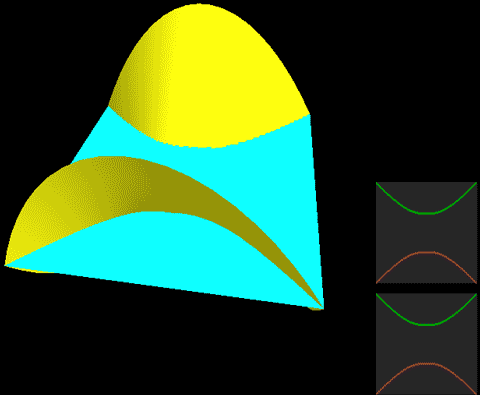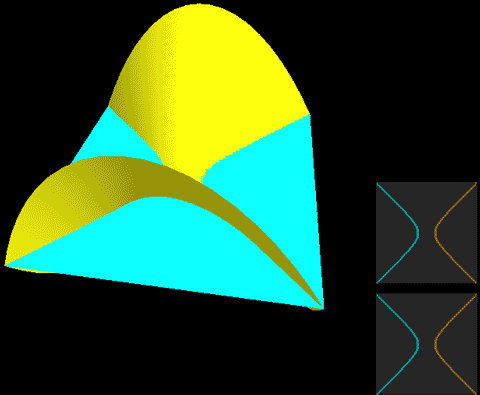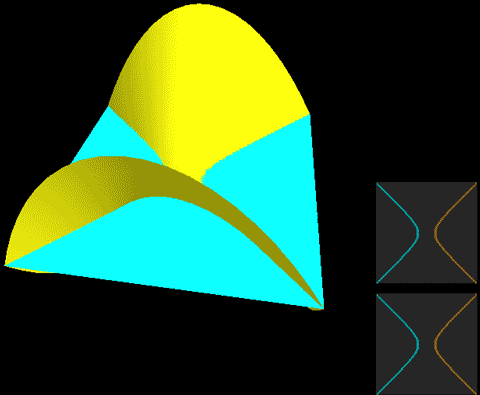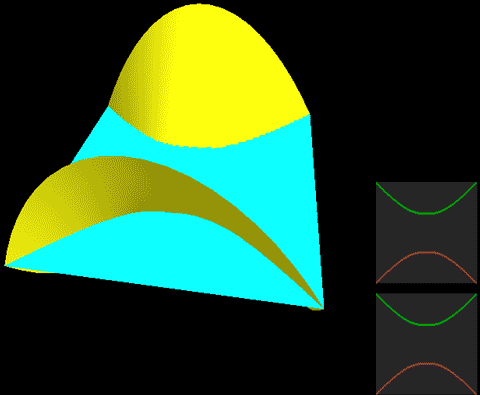
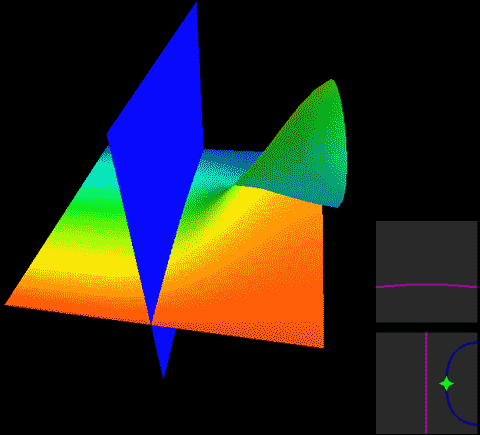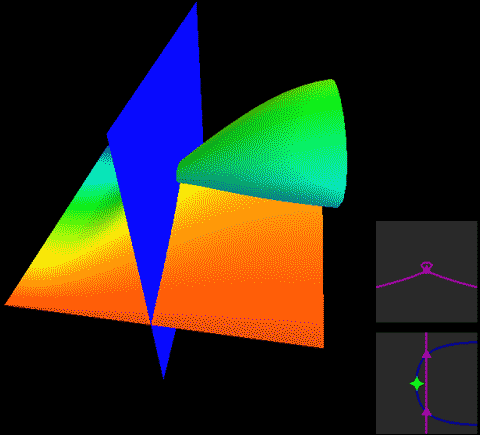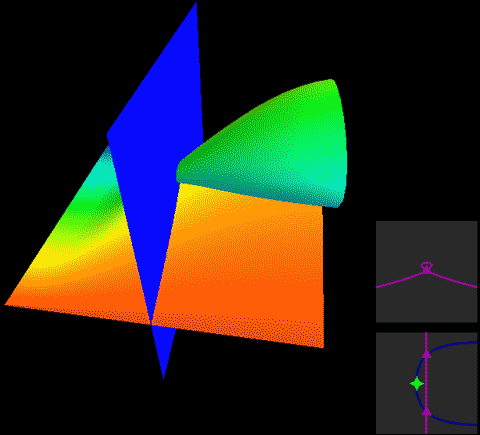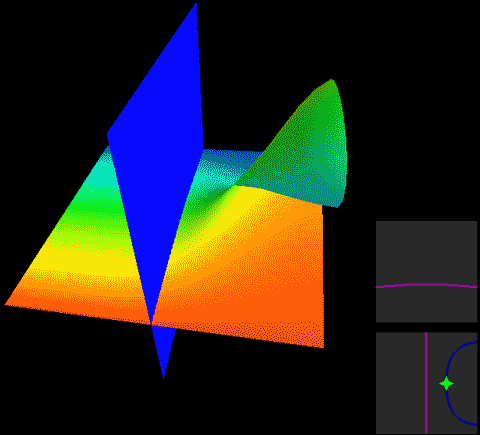
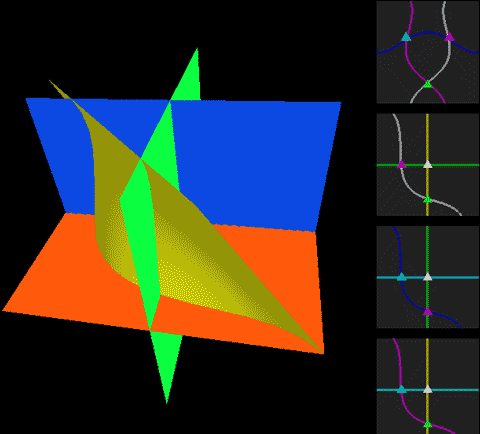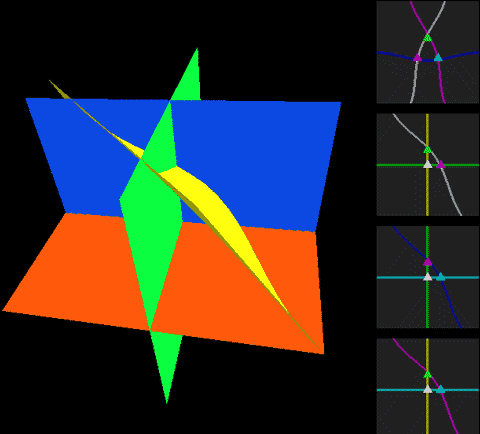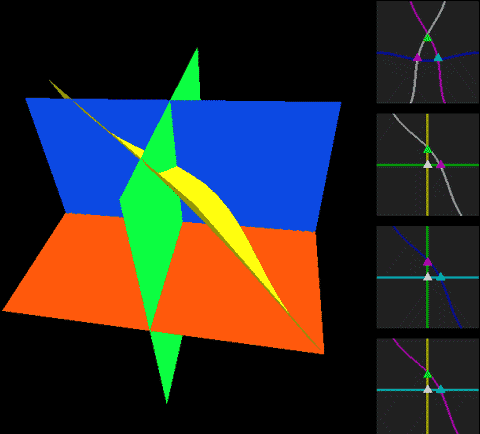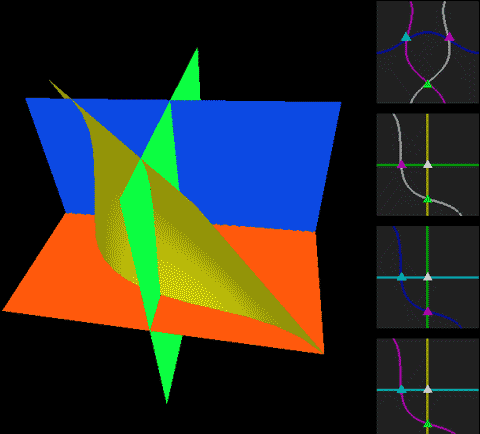
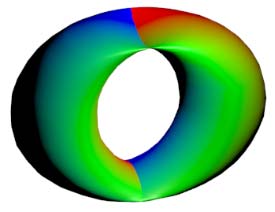
下面,我们把二维球面放到四维空间中,用这种方式来看看球面、无自转的旋转球面结与自转一周的旋转球面结,注意前两个是旋转对称图形,截面不会变化:

我们要证明的就是这个不断自转的公转截面动画的东西可以在不撕破的情况下连续变成一张球面!
两种球面结直接投影到三维空间的样子分别是:

这两幅图的右图将曲面镂空成一条一条的旋转截面切片以便观察曲面内部,而图中旋转截面切片上有一维被压缩了,我们采用上色表示这个方向,因此你会看到每一条切片带子在投影中是自相交的。注意这里的公转自转的关系与地球太阳(不考虑季节的简单系统)有点不同,地球太阳系统中公转自转均平面是绝对平行的,而这个纽结的自转与公转所在平面相差了90度,为半平行半垂直关系。而如果单独把某一点拎出来可以在三维空间中画出轨迹,可以看到地球太阳系统的轨迹有严重的自相交,但自转纽结没有。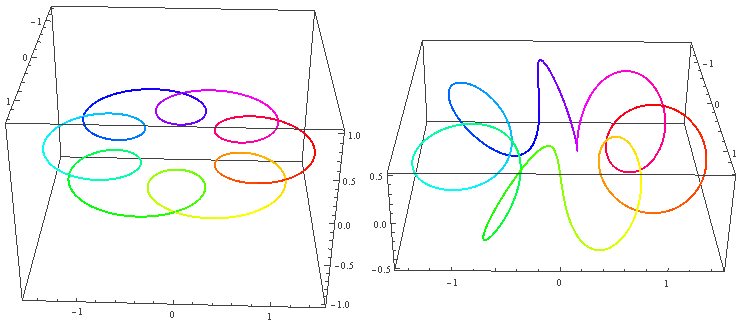
如果你的空间想象力还好的话你应该能想象出无自转的旋转球面结沿着对称轴的截面动画(普通平动),它是普通的死结的截面动画的旋转体(有个普适的结论:截面动画的旋转体是旋转体的截面动画!)。纽结的核心就是投影的交点,所以我们必须要搞清楚这个曲面是如何自相交的,但第二个的结构似乎非常难懂,几乎不可能凭空想象公转加自转的结的投影的重叠方式,所以我们急需一种降维的新方式。幸好我们研究的是拓扑学,研究对象就是个球面,与其在四维空间中研究一个球面结上投影的交痕,不如我们直接把球面像世界地图那样展开,把精力都放在二维空间中,就像给来自二维世界的朋友展示绳圈那样,看看这些交痕展开后会成啥样。
地图上的交线
我们先来看看没自转的旋转结的投影的重合线。还记得三叶结的投影的圆周展开图吗?由于没自转的旋转结的投影是一个完美的旋转体,三叶结始终保持不变,这些交点在旋转过程中也不变,所以我们将得到一些圆周形状的交线,它们展开后是一些纬线。注意标注投影重合时曲面在上方穿过交线还是在下方穿过交线,这里用红色与蓝色区分。
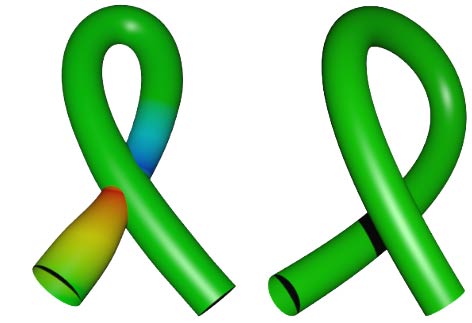
我们再来看一个上期文章中提到的管状球面结,我们接下来试着画这个投影的展开图上的交痕。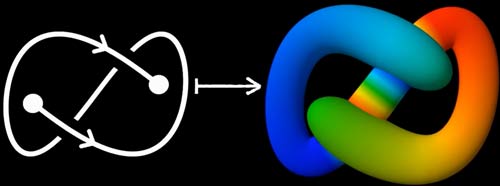
虽然这个管子没有旋转对称性,但我们发现可以按纬线分成一节一节的(下图中黑线),这样我们就可以直接在世界地图上找到对应关系开始画了。(拓扑学嘛,能建立映射关系就行,具体位置摆放不重要)首先我们从绿色的北极点出发,左右侧被管子从中间通过,形成了两个交圆,我们把交圆标注上a与b,并且注意交痕b绿色比蓝色高(红色海拔最高,蓝色最低),因此我们用红线标出,交痕a绿色比红色低,用蓝线标出。接着我们经过黄色、红色,穿过了青蓝色的南极,形成了两个交圆c与d。注意与刚出发被穿过得到的交圆不同,这里我们主动穿过南极,两个交圆是纬线圈,因此画世界地图时两个圈会被剪开变成直线。然后我们从d圆离开,颜色由蓝色快速爬升至红色,来到了之前的a、b交圆,它们现在也是能剪开的纬线圈了,过b圆后,到达南极点附近,该附近还有c、d两个交圆。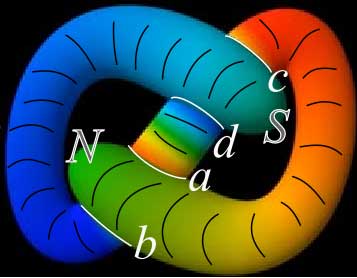
如果你理解了,你应该能画出这么一张地图(注意世界地图方向为上北下南)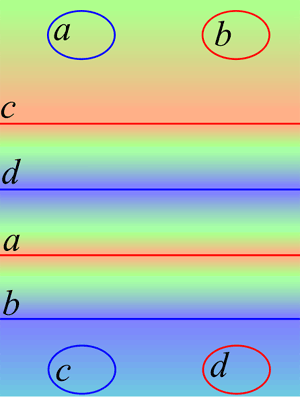
自转的三叶结
如果纽结在旋转中发生自转交痕会怎样变化?显然世界地图上的线条将会变得复杂。注意纽结在旋转时,它的投影一定在做一维纽结的3种合法移动,所以我们需要通过这些合法移动来重构出世界地图上的交线。这好比我们把经度方向作为时间轴,把自转纽结的一维展开图通过添加时间来升至二维。
我们先来照着之前的旋转截面动画把一维三叶结的自转投影过程画下来,可以像动画制作那样只绘制一些关键帧,但这里每一帧都是一个合法移动。绘制这些投影的过程工作量有点大,显得有些枯燥。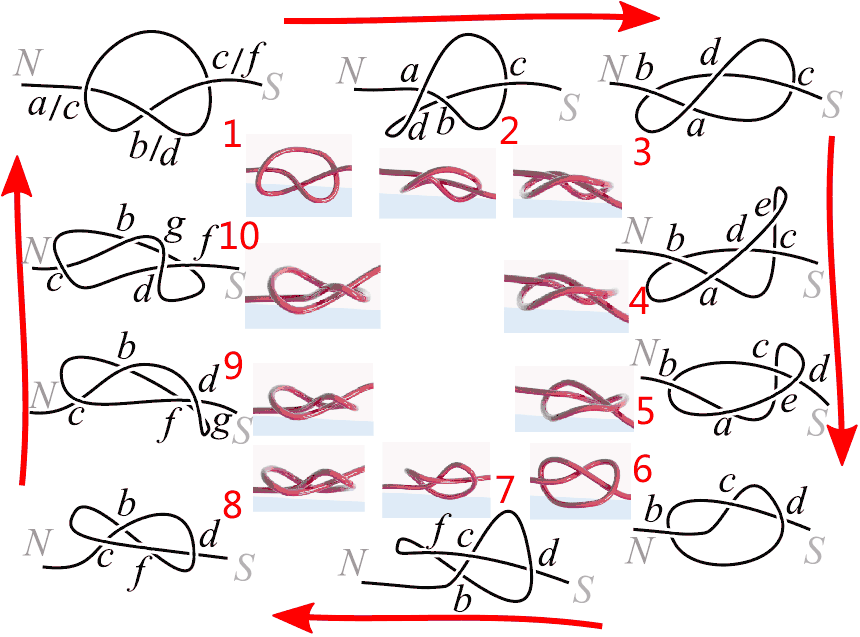
我们看到三叶结旋转一周后,交点的编号变了,但这没关系。先从左上角投影1看起,将交点分别设为a、b、c。投影2在a与b之间插入了一号合法移动,多了一个交点d,注意当交点d产生的瞬间,投影会产生一个“不好的”尖点。投影3对三角形区域a、b、d使用了三号合法移动将其位置“颠倒”,其中投影2变到投影3的某一瞬间三条线会在一点重合。把上面的投影画下来我们得到下图,注意需要标注好投影的三重点的位置与尖点的位置。
图中竖直方向是球面的经线方向,水平方向是纬线或时间轴(旋转的方向),因此垂直的虚线代表某一时刻的三叶结的展开图。比如时刻1对应投影1,它的交点从虚线上从北到南依次可读出,为a b c a b c。时刻2为a b c a d d b c。时刻3为b a c d a b d c。你可以沿着投影1、2、3走一遍验证一下这些字母的颜色与顺序对不对。
让我们从投影3继续旋转,来到投影6,其实中间过程与之前很相似,投影3至4用了一号合法移动产生交点e,投影4至5用了三号合法移动颠倒了三角形cde,投影5至6用了二号合法移动消灭了a与e两个交点,其中两点消灭的瞬间,投影中两条曲线产生了一个“不好的”相切点。我们不难继续画出这部分的地图:
我们现在可以摸清楚这三种合法移动的规律了,其实就是对各部分反复使用前面小节中的这幅旋转了90度的图,现在再来看看它是不是感觉不一样了:
我们把1-10全部画完,可以得到整个世界地图:
注意世界地图东西两侧的连接与投影1交点斜杠两边字母一致,且这些红、蓝曲线其实是画在球面上的。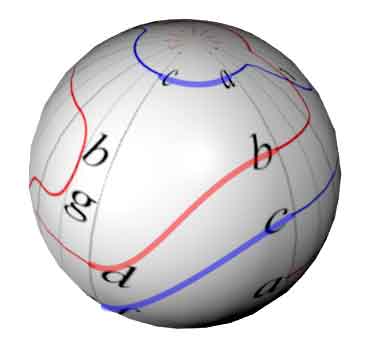
注意刚才我们是以时间轴的视角来看待这幅图的,如果以四维空间的角度看,一号合法移动中产生的尖点对于二维曲面上的分支点,三号合法移动中产生的三重点对应三个二维面两两相交,拥有一个共同的三重交点。而二号合法移动其实并没有产生奇异点,我们从地图中可以看到二号合法移动的交线上没有任何奇异性,只是由于我们选择的坐标不好(有点像黑洞的视界上的奇异性)。
四维空间是各向同性的,“时间轴”方向并不特殊,因此我们可以将上面的世界地图变形化简一下。注意以后我们不再标注投影交点(它必须选取时间轴后才有意义),而是通过三重交点(数字编号)来标注投影中的重合对应点。
七种Roseman合法移动
我们现在已经能够画这些交线了,但当对二维纽结变换视角或拉扯后,这些投影交线的重叠情况肯定就会有变化。之前提到过,类似一维纽结的3种Reidemeister移动,对于二维纽结数学家Roseman归纳了有7种合法移动,因此需要我们研究这7种合法移动对应的投影交线的变化规律。
直接上图吧:
Roseman移动1投影中有分支点,可能不是很直观,上一期文章说过可以利用截面法来理解这个Roseman移动。
Roseman移动2投影中有分支点,也是通过截面法来理解这个Roseman移动。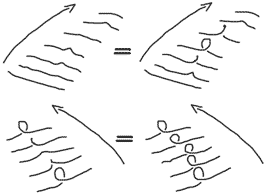

Roseman移动3是最好理解的了,因为两张曲面第四维颜色为常数,只需要关注三维投影上的截痕变化。
Roseman移动4中两张曲面第四维颜色也为常数,只需要看三维上的截痕,也很好理解。

Roseman移动5中所有曲面第四维颜色都为常数。
Roseman移动6中虽然有个曲面有分支点,但另一个平面为蓝色,说明在第四个维度的最后方,前方带分支点的曲面的移动当然不会影响后方的平面。
Roseman移动7虽然有四张曲面参与,但所有曲面第四维颜色都为常数。
利用Roseman移动解开它!
热身
我们先不着急,在正式解开旋转球面结之前,先解决其他一些简单的问题(或你可以先独立尝试解旋转球面结):
- 上期文章绘制过平圆环的投影图,我们用交线的Roseman合法移动来证明该投影能够在四维空间中拉扯为一般的轮胎环面。
圆环的展开图是一个矩形。该平圆环的三维投影有两处平行于经线的二重交线与四个分支点,展开后如图所示:
根据Roseman移动2,两个分支点可以在方向一致的情况下相互融合,我们得到两个圈;最后我们发现这两个圈可以用Roseman移动3移除,至此三维投影中所有的交痕都消失了,也就意味着该投影变成了没有任何自相交的轮胎环面。 - 克莱因瓶是无法嵌入进三维空间的,除非允许自相交,常见的自相交模型除了穿过自身的瓶子形还有下图这种,我们用克莱因瓶上交线的Roseman合法移动来证明两者拓扑等价。(其实我们还证明了它们在四维空间中同痕,即可连续地将一个变为另一个)

这个投影与平圆环的很像,区别就是它只有一条二重交线与两个分支点,比平圆环的少一半。我们直接用Roseman移动2把这两个分支点融合,得到两个封闭的圈,其中一个是正常的小圆圈(红色),另一个圈则跨越了整个经线无法缩小(蓝色)。红色对应克莱因瓶肚子上的交痕,蓝色对应克莱因瓶颈部上的交痕。 - 上期文章提到,即使固定死管子两端口,穿过自身的管状结是可以解开的,直接想象解开过程有点困难,我们不妨同样用交线的Roseman合法移动来证明。
首先我们观察到管状结上有两个交痕,我们从左至右标记为A与B,从管状结左边管口出发,穿入穿出自身,得到贯穿性交痕A与B,然后绕过来被自身穿过,得到两个非贯穿的圆形交痕。我们先使用Roseman合法移动2,将交痕B拆成一对分支点出来,然后再对A、B交痕使用Roseman移动4,将两个交痕连接起来,整理一下发现现在的交痕为有一对分支点的圈,与Roseman移动1一致,可以收缩消失。
下面我们就要解球面结了,强烈建议自己可以先试一试,解结步骤并不唯一,因此下面只是我给的参考。
解开球面结
根据上面三道题的经验,我们先直接尝试合并分支点。观察发现,下图中两边标有1与4的分支点可以碰面,而两边标有2与3的分支点也可以碰面,要记住这是球面的展开图,因此我们可以像跨过“国际日期变更线”那样去另一边。
我们先用Roseman移动2合并两边标有1与4的分支点。
再合并两边标有2与3的分支点,注意交线是如何跨越“国际日期变更线”的。
球体的展开图因“国际日期变更线”的存在确实看起来不方便,我们不妨把对应两边直接连起来,把它变成像球极投影图那样,只要交线不过极点地图就没有任何边缘了。注意选择从上面绕还是下面绕与球极投影北极点选择的位置有关。
我们稍加整理,可以得到下图中4个“8”字形的交线,它们首尾相交成环形,也就是说,现在所有交痕都只有二重交线与三重交点这两种了。
在我们继续找能用的Roseman移动前,我们先要明确一下这幅图是展开图,实际上交线上各点之间是有相互对应的关系的,让我们再观察一下一个有意义的交线展开图有哪些性质,免得错误使用Roseman移动后还不知道。
- 首先,我们已经用数字标出了一共有4个三重交点。虽然4个“8”字形的交点一共有12个,但带相同数字的位置在球面折叠起来后却对应三维投影空间中的同一个点。我们还可以观察到这些标有同样数字的三重点一定有一个是全红色线相交、一个是全蓝色线相交、一个是一红一蓝相交,因为它们必对应着第四个维度上最前面的曲面、最后面的曲面与夹在中间的曲面。
- 当我们离开一个三重点沿线走时,这条线是两张曲面的交线,因此展开图上将会存在成对的红色与蓝色交线。如果我们来到了下一个三重点,则展开图上的两条交线也会来到这个点。比如下面的红色八字形,它可能与上面或右边的蓝色八字形成对,但到底跟哪个配对呢?我们沿下面的红色八字形转一圈,经过的三重点是2-1-3-2-4-3,上面八字形从2出发,我们也能得到2-1-3-2-4-3,而右边八字形顺序不管什么方向绕都不能与2-1-3-2-4-3匹配,所以上下八字形成对,同理可验证左右八字形成对。
- 虽然现在分支点已被我们消去了,但从之前有分支点的图中可以看出,分支点是一个特殊的点,成对的红色与蓝色交线从这里发出,分支点与自己对应,这里开个脑洞:分支点有点像电影《信条》里面的时间逆转机器,红色线过去后就会变成蓝色,并且所有经过的三重点会像时间倒流那样以相反的顺序经过。
由于不涉及分支点,我们可以试着使用Roseman移动4、5、7来解。Roseman移动4可以将两条颜色相同的线段重新连接,但必须要同时改变成对的红色与蓝色。乍一看很容易实施Roseman移动4,但同时满足这两个条件的移动并不多,比如你如果想沿着黑色箭头方向对红色的1-4与3-4使用Roseman移动4,那么你还必须要对蓝色的1-4与3-4使用Roseman移动4,但可惜它们中间有其他交线,无法做移动。这里还要注意右边8字形上有两个蓝色的1-4线段,怎么知道哪个是要找的成对的线段呢?我们注意到其中一条线段从1继续延伸走到3,另一条从1继续延伸则走到2,而我们选择的红色线段从1继续延伸走到3,因此前者与选择的红色线段成对。
那有没有能够做Roseman移动4的选择呢?是有的,我这里标出了一些选择(其实应该还不止这些):
决定做哪个选择之前我们来看看Roseman移动5与7。Roseman移动5要么找三对平行线,让它们相交得到三个“二边形”区域,要么找三个符合对应关系的“二边形”区域把它们解开成三对平行线。而两个8字形连接出正好就有一个“二边形”区域,但遗憾的是,这些“二边形”区域对应不到另外的“二边形”区域,因此没有一个“二边形”能使用Roseman移动5解开,比如下图。那我们能不能选三条平行线用Roseman移动5让它们相交得到三个“二边形”区域呢?这样交点数变多了,与解结背道而驰,因此我们放弃Roseman移动5。
再来看Roseman移动7。Roseman移动7也很有特点,它需要找四个有对应关系的三角形结构,我们发现,画出左上角阴影三角形134的对应边后,对应边与2号三重点均能构成三角形,因此符合Roseman移动7。
现在摆在我们面前的是Roseman移动4与7。我们先看Roseman移动4。
我们先做A移动与B移动,发现好像没什么进展。
如果换做C移动,我们可以把两个8字形连在一起,并且我们发现,产生了可以使用Roseman移动5的三个对应的二边形。
那我们接着做Roseman移动5吧,看看能不能解开。我们发现移动后的图形已经变得很简单了,是两个打结的圈,为了解开,我们用Roseman移动4将圈一分为二,然后发现又可以用Roseman移动5,最后得到四个分离的圆圈,我们用Roseman移动3就把所有交线消灭掉,至此,我们完全解开了旋转球面结。
另一种解法
如果我们用之前提到的Roseman移动7,会把4个8字形套在一起,不会简化问题。那是不是上图就是唯一解开旋转球面结的方法步骤呢?当然不是,那只是我个人琢磨出的一种步骤。其实这个Youtube视频里展示的步骤是直接用Roseman移动4与Roseman移动5后,再用Roseman移动1消去分支点,而本文第一步就消去了所有分支点,步骤比Youtube视频中的要多一些。
注意由于我们是在球面上,那个大的带分支点的环可以经过北极点从而与内部的环分离,因此这是典型的Roseman移动1的情形,可以直接消掉所有交痕。
好了,本文就到这里了,至于怎样证明旋转两圈的结无法解开则是下一个话题了,虽然这篇文章中描述的拓扑形变都发生在四维欧几里得几何空间之中,但可能有人不喜欢拓扑学,以后可能的话,关于拓扑学我将新开一个系列的坑。