这篇文章是参观四维国的延续。在那篇文章里，我提到了四维的城市交通不需要修立交桥，因为地面是三维的，两个方向的车流只需要走异面直线就对了。现在我们先研究一下四维国的公路到底是怎么样的，汽车怎么在上面开，以及三轮车、自行车在四维空间中的类比。研究四维的一般物体不能用球极投影，因为球极投影本质是研究超球面，我们要把正多胞体投到超球面上。所以我们从截面法和投影法入手。先看看三维的一条笔直的带街沿的路：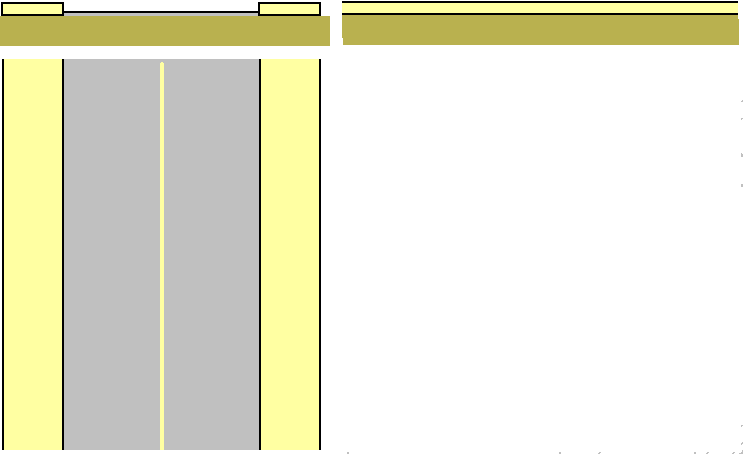
我们看到俯视图是最清晰的，除了看不出来街沿有高度。四维的道路呢？它的俯视图是立体的柱形，但底面该是正方形吗？或者圆形让路变成圆柱？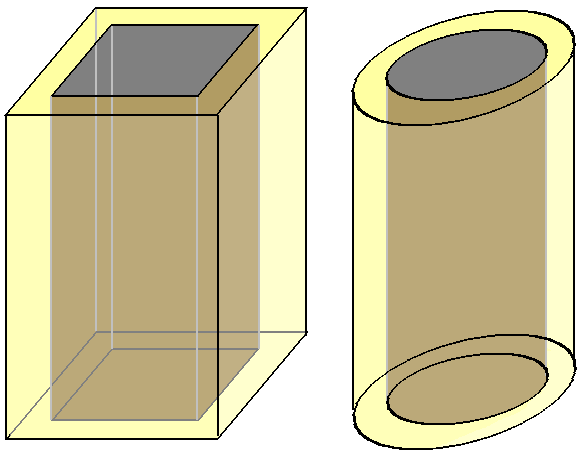
我们看到由于多了一维，道路的二维截面形状问题开始变得有意义（一维连通的图形只有一种：直线段）。注意我把路画成透明的只是为了观测方便，其实四维人能够直接看到三维的画面，不会被遮挡，它们会看到街沿上每点都是均匀的淡黄色，路面是均匀的灰色。四维人不用过马路，他们直接可以从街沿上绕过去！注意不是翻过去或修了天桥，因为这是俯视图，重力与投影中所有方向都垂直。那如果不修街沿呢？那是不是就得过马路了呢？其实也不用过。车辆都集中在柱形里，你只要从边上绕着走就没事（虽然有点风险）。那正方形和圆形截面的道路哪个比较好呢？车道（比如中间是否该有一条线）怎么划分呢？这两个问题其实是相关的，我们放在以后讨论。
四维车轮
在讨论这个问题之前，我们先看看汽车的形状和构造。二维世界中车两个轮子就够了（但似乎无法把轮子固定到车上），三维车得要四个轮子：（先暂不考虑其它轮子更少的交通工具）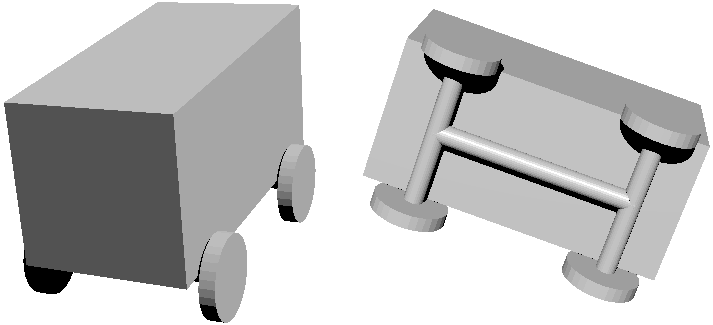
我们看到车体是放在连接了四个轮子的底盘上的。就像超立方体的类比，我们自然认为四维车需要八个轮子，分布在长方体的顶点上，而上面的车体则可以近似成超长方体。我们来看看四维小车的俯视图：但超长方体车体在上面会遮挡住下面底盘结构，我们先单独把底盘结构拿出来。但此时有个很严峻的问题：轮胎的形状。我在参观四维国中已经分析过，要想能控制住车的运动，轮胎只能有一个方向的滚动自由度（比如我们世界里从来没过车有球形轮子），这种图形便是圆柱（实际轮胎圆柱边沿是平滑的，应该算作圆环形了，我们先不考虑这些），但到了四维空间，圆柱形却是一个家族：常见的有方圆柱（圆柱柱：Cubinder）和双圆柱（两个圆的直积形：Duocylinder），我们又面临着像选道路截面那样的问题。将它们侧放在三维平面上，从俯视图来看一下它们是怎么滚动的：首先我们要明白怎样“侧放”才能让物体滚动。比如圆柱立着放（圆形面朝下）是滚不动的，所以柱形的圆形底面不能朝下，得侧着。再看圆柱的高，它是线段（比如下图左边灰线），到了四维，圆柱柱有两条高，围成正方形，但这种侧面的图形可以是任意的，如果取圆，就叫双圆柱。双圆柱的底面侧面是对称的，不管怎么放都可以滚动，但是原理和圆柱柱一样，只能在一个方向上滚动。
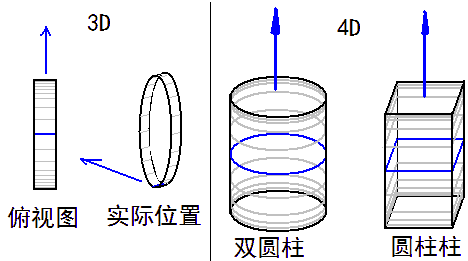到底那种轮胎好呢？其实侧面高的形状不参与滚动，选什么图形都无所谓，但联想到真实轮胎圆柱边沿都平滑得快成圆环形了，所以我认为选择棱角更少的双圆柱更好。
准备工作都做完了，下面开始构造四维车的底盘，它的俯视图是这样的：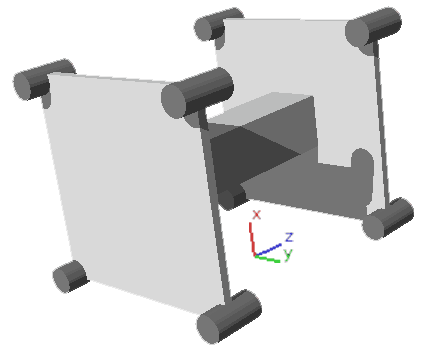
为了方便描述，我建了直角坐标系xyzw，其中w方向是竖直方向，俯视图画不出，剩下的xyz方向就是三维地面的方向了。由前面的准备工作可知，现在四维车可以运动的方向应该是侧面的高（投影里面的圆柱底面）垂直的z轴方向。这辆车有四个前轮四个后轮，分别由两个正方形的板子连接,然后中间有连接前后轮的轴。其实用板子还是用十字形连接这些不重要，只要能把八个轮子固定就行。你或许有疑问：怎么解释正方形的板子的角插进了圆柱里面？其实这跟三维轮子的轴一样，俯视图看到轴插进了长方形里面，而旋转发生在zw平面方向上，剩下的方向保持不动，即平行于侧面高的二维平面xy，相当于轴，正好是正方形的位置。当然，轴也得是圆的，所以你看到俯视图中正方形的薄板其实是一个直径很小的圆柱柱（其直径等于薄板厚度，两条互相垂直的高就是正方形的边长）
下一个问题来了：车辆不能一直走直线，得能控制转向。我们先来看看三维的小车如何转弯：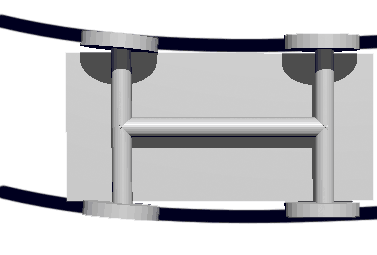
图中标出了两侧轮子的转弯路径。两个前轮起引导作用，两个后轮跟随。同样对于四维小车，我们只转动四个前轮，四个后轮不动。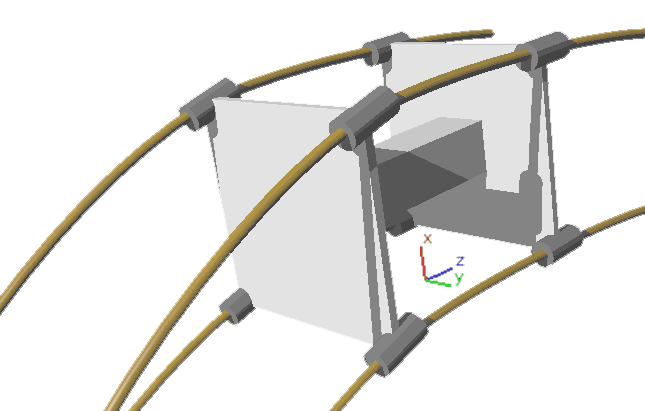
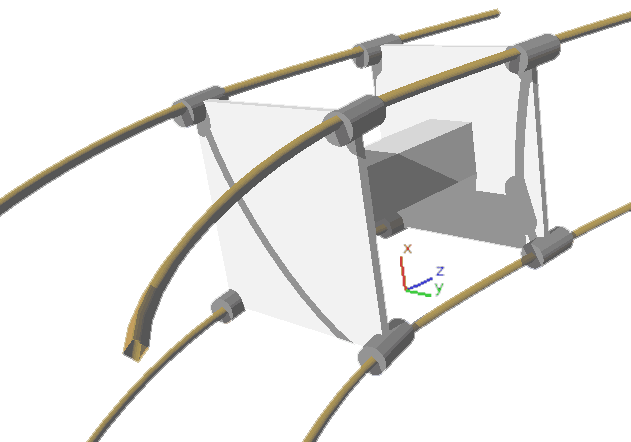
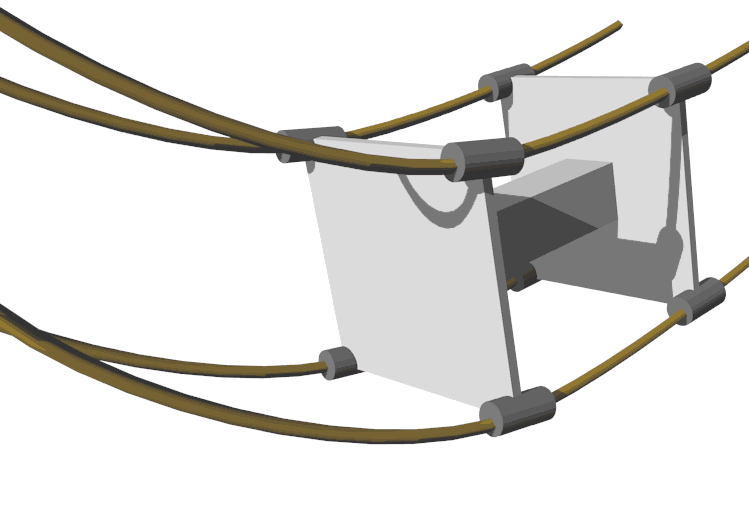
其它造型的四维车
其实小车不一定只能往x轴、y轴方向转弯，只要是地面上垂直于z轴的方向都能转。所以这启发我们其实可以造一种“六轮车”——车轮顶点分布在三棱柱的顶点上，它和八轮车的性能几乎是一样的，只是八轮车更加稳定。当然N轮车都是可以的，甚至你可以前轮N个，后轮M个搭配着设计，或是让N趋于无穷——把所有轮子连在一起——这也是可行的，因为这些都是侧面不参与旋转的高的方向的图形花样，不影响轮子转动，唯一不好的就是转向可能太笨重了，后轮使用这种轮子是没问题的。这些花样就像我们见到的有着很多并排着的轮子的卡车那样，要么增加稳定性要么增加负重能力。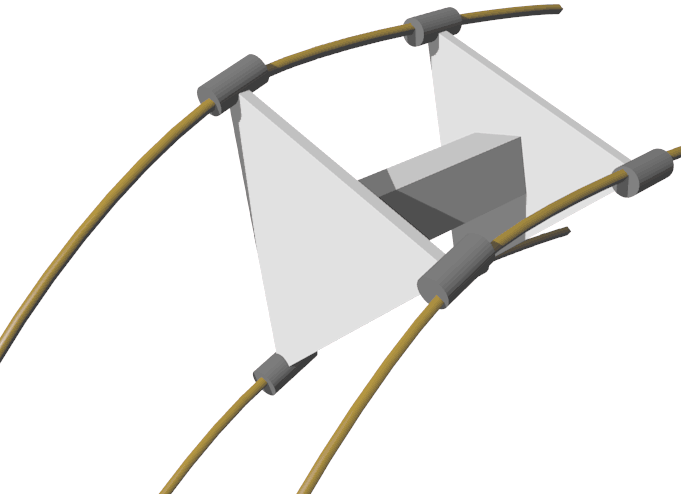
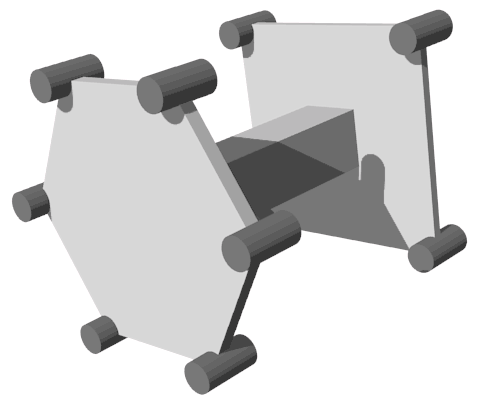
还有没有其他的运动方式？我们知到，三维车只能左转、右转，因为地面是二维的，平面上只允许顺时针逆时针两种转动方向。那四维车的转向模式就应该与三维空间的所有旋转方向都有对应：比如前面看到的两种转弯模式对应绕x轴旋转和绕y轴旋转，那么还剩一种旋转：绕z轴对应哪种模式？z轴是前进方向，所以这种旋转是一种自转，就像翻滚着往前飞的战斗机那样，轮子的轨迹是螺旋形。我们之前设计的小车能否胜任这种转向呢？答案是可以的，虽然不太好想，这里先留给读者思考，答案在文末。总结起来，四维小车的控制类似于飞船的控制——可以在三维地面空间中无重力自由翱翔，去四维世界旅游想自驾的话估计要飞行员的驾驶执照才能开他们的车。
四维自行车
至于自行车，我认为可以分为二轮和三轮的，它们静止时都不稳定，有倒的可能。但具体哪种好控制方向，哪个稳定性强等问题已经超出了我的无力认知水平，这里就不再讨论了。
我没有画出踏板结构了，这部分设计也太难了，它牵涉到四维人腿是怎么长的……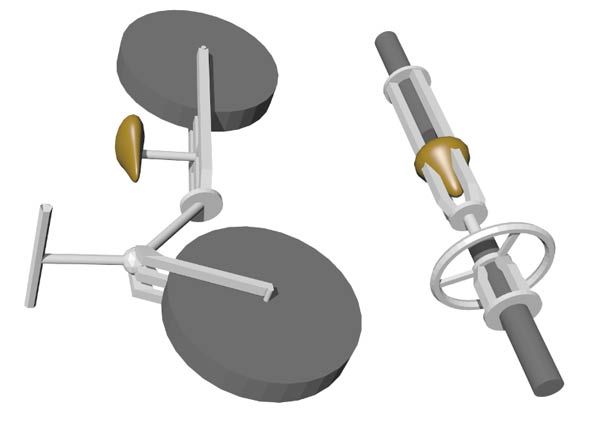
三维自行车的方向盘只是一个一维的龙头，是方向盘的简化版；同样四维自行车的龙头也是一种简化版，但它也是二维的，看上去像是我们轿车的方向盘，但实则不然：转弯时把它掰歪（如下如），而不是以侧视图中间的轴为中心转方向盘，这可能可以让自行车做自转的转向，但摩擦力很大，具体能不能实现我还不清楚，我暂且认为不能，因为你必须有一定速度转动方向盘车才有可能跟着动，而把方向盘打到任何位置不动车都会停止自转。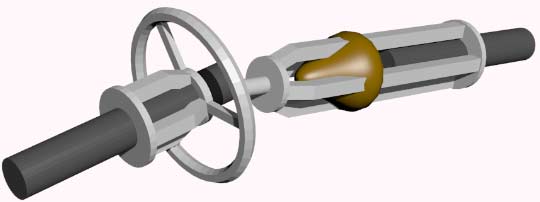
但三维三轮车直接放到四维空间却变成了会倒的三轮车：你可以把下面的侧视图看作三轮自行车倒在地上的俯视图。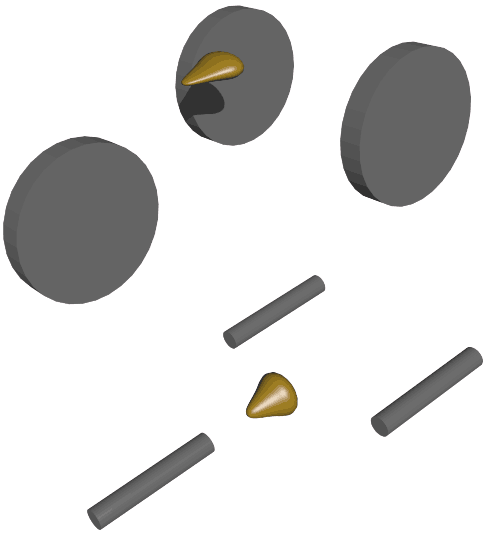
说到这里，想必稳定的三维三轮车类比也是显而易见的了。三轮车之所以要三个轮子，是因为三点确定一个平面，这样构成三角形车才能在地面上放稳；四维世界中的类似物是四轮车，轮子分布在四面体上。我们仍然固定后轮，只留一个前轮导向。但四轮车的缺点是可能无法方便地控制自转，原因和自行车一样。这是四维空间不会倒的所需轮子最少的车：如果强行翻倒四轮车，把下面的侧视图看作三轮自行车倒在地上的俯视图，中间的后轮就具有高度（与投影垂直，看不出来），所以要翻过来要花力气克服重力，就像你推翻三维世界的三轮车那样。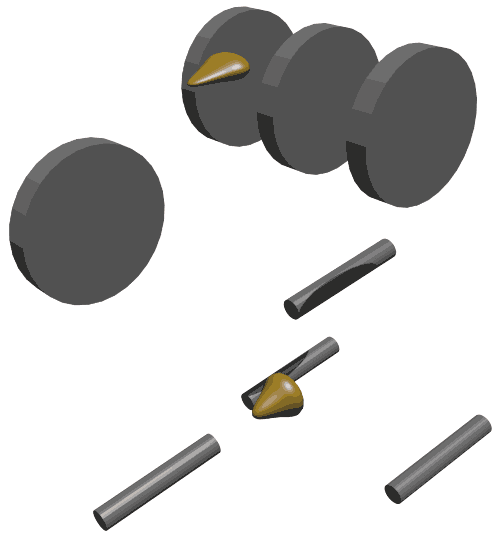
汽车转向系统
我们来讨论一下汽车方向盘的设计：根据类比，汽车方向盘应该是球形的，可以绕着一根轴旋转。原来《流浪地球》里面的重型运输车辆就是四维的！我们说过，四维空间中的旋转是绕着面为轴的（或双旋转那种找不到旋转轴），然而球体具有很高的对称性，在四维空间它有着垂直于它所在空间的旋转对称轴。我们可以这样做一个球柱形的杆子将方向盘的运动传送到底部。
我们先来看一看三维车最简单的转向系统：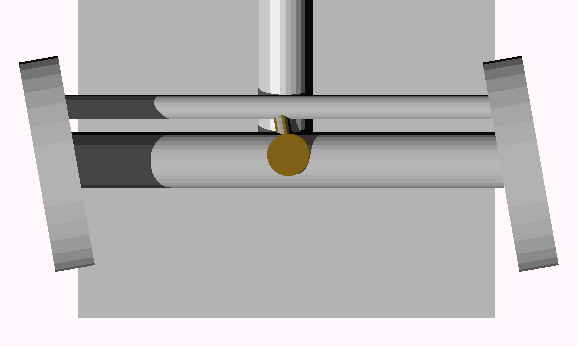
类比得到四维车最简单的转向系统：（我把中间的梁画成半透明的以便观察）
跟三维情况差不多，但还记得我们之前留给你思考的自转模式吗？只需自转方向盘（绕方向盘的竖直轴和前进方向张成的平面转动）就行了。其特点是每个轮子朝向不同，每个轨迹都是螺旋形，这就是前面提到的小车所有可能的转向和三维空间所有可能的旋转对应。二轮、三轮自行车和四轮车可能都没法很好地做自转，因为它们唯一的前轮只能处在转轴上。但注意，并不是只要前轮有两个或以上的轮子就可以做螺旋运动（比如两个轮子的轨迹对应DNA双螺旋结构的样子）自转不同于一般转向。当3D/4D汽车左转时，两个/四个前轮往左斜，后轮保持方向不动，这样前后就形成了角度差。但自转的螺旋运动是靠四个前轮的相互角度差实现的，自转的轨迹对于前后轮都是螺旋形，所以如果后轮保持方向不动则会导致轮子被撇住——如果你是在无法理解可以想象一下左转弯只有左前轮转向，但右前轮往前的情形。所以四维车的前后轮必须都要能活动，除非放弃自转转向这个功能。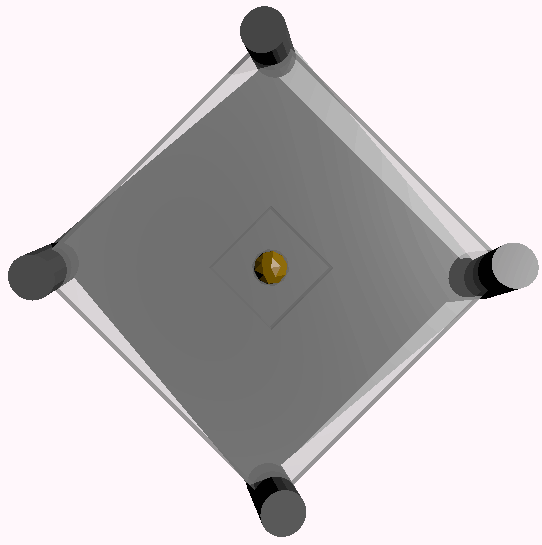
四维空间中的公路交通工具我们就说到这儿了。如果大家有什么新的想法或异议都欢迎来讨论！下一步我们将设计四维公路上的车道划分、道路设计和轨道交通系统。
更新
四维汽车模拟器已经完工啦！基于牛顿力学的物理引擎可以验证以上关于汽车转向的方式。你能把车开出隧道吗？
