四维世界（十三）：五维时空
（注意：如果你还在纠结疑惑第四维该是空间还是时间，强烈建议先不要阅读本文，否则会更晕）
这次我们来看看四维世界，或者说，应该是四维世界所在的宇宙的物理定律：五维时空(4维空间+1维时间)中的广义相对论和旋转黑洞的结构。我不是物理方面的专业人士，本文仅将相关文献汇总来大至勾勒出对五维时空的认识。按照惯例，我们先来简单过一下现实世界四维时空中的相对论。
四维时空相对论简介
相对论与黑洞这些内容确实有点晦涩难懂，这个简介估计都要占全文的一半篇幅……我尽量说说核心“设定”。不想了解相对论可以直接空降到五维黑洞章节，后面有很多渲染图，这里还有Tesserxel上的黑洞体素渲染链接，点击右上角Black Hole跟Black Ring场景即可。
狭义相对论
现实世界中的相对论分为狭义和广义两种。狭义相对论最核心的设定就是：光速在任何参考系下测量都一样：你追着光跑，光还是比你快同样的速度；迎着光跑，光向你逼近的速度也不会更快。这怎么可能呢？那只能是高速运动下，空间会收缩、时间会变慢，从而保证光速不变。这些时空缩放变换很难以理解，更自然的描述方式是数学中的闵可夫斯基空间（简称闵氏空间）几何：在这个空间里的长度度量很奇怪，勾股定理变成了直角边平方差等于斜边，最对称的圆形变成了双曲线，详见之前的文章《闵氏空间与常曲率空间的几何》。相对论中，运动物体的速度在时空中不直接叠加，而是叠加类似旋转角度那样的双曲角（叫做快度）。结合闵氏几何来理解狭义相对论并不难，网上关于狭义相对论可视化的资料也很多，就不赘述了。
引力就是时空弯曲
狭义相对论描述的是没有引力、平直的时空，所有的物理定律都在闵氏空间中描述，具有闵氏空间中的“洛伦兹”对称性。但爱因斯坦发现，引力并不是一种在闵氏空间中能描述的“力”，而是一种时空几何效应：物体让闵氏时空弯曲，而弯曲的时空又引导物体的运动轨迹。在数学语言里，物质与能量（包括电磁场）由能量-动量张量来刻画，时空的弯曲由 黎曼曲率张量来描述。通过比较牛顿引力的形式和能动张量的结构，爱因斯坦提出了著名的爱因斯坦场方程，把物质分布与曲率分布相关物理量用等号连接在了一起。
时空弯曲简介
狭义研究平直时空，广义研究弯曲时空：弯曲体现在影响物体之间的距离、角度之上。最简单的纯空间的弯曲例子就是平面和球面了，平面是平的、球面是弯曲的，很形象直观，但广义相对论的时空弯曲不是这样的。广义相对论把三维空间加一维时间作为一个整体的四维时空看待，如果把宇宙比喻成一张纸，那么这张纸就是四维的，纸上的一个个点代表时空中的一个个事件。在大质量天体的附近时空（纸）会弯曲，远离的地方这张纸就是接近平直的，即在“纸面上”沿时间与沿空间方向都是平的。
内/外曲率的区别
按照我们的经验，低维的物体一定要在更高维的空间中才能弯曲，这种看法下，我们的四维时空宇宙都要处在至少五维空间中才能实现弯曲。然而曲率分内外曲率两种，按外曲率理解是这样的，但广义相对论的曲率是内曲率，结论不一样，下面解释两者的区别：
- 想象你拿着一个高科技的柔性屏手机，上面正在运行一款2D射击游戏，不妨把游戏世界当成一个宇宙，这是个二维空间+一维时间的三维时空，为了好理解，我们先忽略时间只考虑空间曲率。注意屏幕只是显示设备，屏幕卷成一个圆筒后，并不影响游戏世界的运行逻辑（即这个世界的物理学），但我们会看到整个二维游戏世界在三维世界里确实弯曲了，且世界的物理定律好像都变了：游戏子弹的轨迹不再是真正的直线，这些直线随着屏幕的卷曲变成了曲线，（废话子弹不可能飞出柔性屏），但游戏里的人物（如NPC）丝毫不知道屏幕卷起来了，它们发现不了这种外曲率。再狠一点，我们把屏幕戳烂一个洞，也不影响游戏的内在逻辑！我们所在的宇宙会不会也被卷曲了但我们也不知道呢？其实这些外曲率是没有任何意义的，宇宙外的空间与拿手机的人更像是一种独立于宇宙假设出的“上帝”的感觉，我们没必要相信存在一位荒唐的上帝正在折叠我们的宇宙。
- 然而，如果游戏里的NPC测出三角形的内角和大于180度，就暗示着他们不可能生活在平面上，可能生活在球面上，或是其它东西上，注意这是一种在他们看来“活生生”的内部曲率效应，跟显示设备无关，里面的NPC能够在游戏世界的逻辑上测算到这样的曲率效应。想象你在一个三角形内角和大于180度的宇宙中生活（曲率带来的局部度量不同），且你无论朝那个方向走远了会发现又会回来（整体的拓扑结构不同），这大概率就是一个球面，这个宇宙是封闭的、体积有限的球面，但球心对于你来说是没意义的，球体的“内部”空间也没意义，那为什么我们要说它是球面呢？因为这个宇宙的内曲率恰好跟真的球面的内曲率效应一样罢了。由于外曲率的无意义，内曲率才有绝对意义，数学上干脆把内曲率效应一样的空间视为同一种空间，因此干脆就叫它球面宇宙了。
回到四维时空的弯曲上来，宇宙的意思就代表着全部的最大空间（时空），它应该无所不包，黑洞对时空的影响就是改变时间流速（距离），改变对空间时间方向的感知（夹角），这些效应是妥妥的内曲率效应，如果无法去到也无法观察到宇宙之外的东西，高维空间是一种没有用的假设，因为你无法证明它存在也无法证明它不存在，根据“奥卡姆剃刀原理”，我们最好去掉不必要的假设，相信不存在第五维空间（注：这是在没考虑弦论的前提下，弦论认为还有更多的微观“卷曲维度”，这里暂不讨论）。科普中的虫洞空间折叠的折纸比喻只是利用空间的内曲率以及空间之间的连接关系与折纸模型的相同，这样才利于向听众解释。
四维黑洞简介
爱因斯坦方程是高度非线性的，解起来非常困难。但物理学家们还是在二十世纪逐步找到了几个经典解：
施瓦西(Schwarzschild)解：这是第一个黑洞解，描述了一个没有电荷、没有自转的球对称黑洞。它的结构简单，只有一个球形的事件视界（即黑洞的边界，进去了就出不来）和一个中心奇点（飞船/任何物体碰到它将会从时空中消失）。
Reissner-Nordström解：考虑了黑洞带电的情况。虽然整体还是球形，但跟施瓦西黑洞不同的是，它有内外两个视界，只有在两个视界之间才是只进不出单向的，进入内视界里面后反而能自由移动了。
选读：裸奇点与宇宙监督假设
当黑洞带电足够多时，内外两个视界的半径会互相接近，直到最后消失。这样只进不出的单向区域也消失了，里面的奇点直接暴露在了我们的宇宙中。奇点的性质是很糟糕的，这种没有视界包裹的裸奇点会导致物理规律失去预测能力，因为奇点附近的因果结构完全破坏。貌似我们可通过往黑洞里大量投电荷来制造裸奇点黑洞，但电荷增多后斥力越来越大，可以证明到一定程度后就无法再克服斥力往里面扔电荷了，因此造不出裸奇点。物理学家彭罗斯提出了著名的宇宙监督假设：自然界中不会允许裸奇点的出现。克尔(Kerr)解：描述了旋转黑洞。与静态黑洞不同，旋转黑洞的结构更为复杂：它同样有外视界和内视界，外面还有无限红移面（也叫静界）这样的特殊区域。在外视界与无限红移面之间的区域叫能层。虽然能层中的飞船有逃离黑洞的可能，但不能悬停保持静止，必须随着黑洞方向一起旋转，即黑洞把空间带转了。能层体积反映了黑洞的旋转动能：不旋转的黑洞的视界跟无限红移面完全重合，能层体积为零。克尔黑洞的内部并不是一个奇点，而是一整个奇环。由于奇环的存在，时空可以继续穿过圆环进行延拓，即出现虫洞结构来连接到别的宇宙。事实上这些延拓属于最理想化的数学推演，在真实的物理环境下，任何微小扰动（例如量子效应）都可能使这些“虫洞”不稳定而崩塌。但至少在方程层面，它展示了广义相对论所允许的丰富而离奇的几何结构。Hadroncfy很久前写的《黑洞之旅》，以观光者与导游的视角介绍了从外面进入克尔黑洞全过程将会看到的景象，对于不想看任何公式的读者来说值得一读。
克尔–纽曼(Kerr-Newman)解：带电又旋转的最一般的黑洞情形，同样有上面的视界、奇环等结构。黑洞无毛定理表明，黑洞只有质量、角动量以及电荷三个守恒量，其他的信息全都丧失了，几乎没有形成它的物质所具有的任何复杂性质，黑洞不存在如菱角、纹路山脉或其他有凸起的形态。
这些黑洞解不仅在理论上重要，也在天体物理学中有着对应意义。例如，人们相信大多数星系中心的超大质量黑洞都是旋转的（接近Kerr解的情形）。
度规：描述弯曲的手段
黑洞有些性质非常神奇又难以理解，如当你从远处观察一个物体掉入黑洞时，它似乎永远也掉不进黑洞！你会发现靠近视界的物体的时间流速会越来越慢，但实际上，从物体自身的视角，它会在有限时间内落入黑洞，且落进去的瞬间不会感到任何异常。然而一旦穿过黑洞的事件视界，常规的空间和时间的概念就被颠倒了：时间方向开始像空间一样受限，而原本空间的径向方向变得不可避免地“向内”流动。换句话说，你再也无法停留或向外逃跑，因为“向外”已经变成了一种不可能的空间方向。我们很难用日常经验去理解黑洞内部的运动规律，要想清楚就必须学习描述时空的语言——度规。
度规用于确定时空中如何度量各点的距离。这里会介绍一些技术细节，要求会求导和全微分就行，不需要懂微分几何。由于弯曲的时空局部是平直的，所以我们只用描述其微小长度的计算方式，通过积分就能得到所有曲线的长度。举几个例子：
- 平面：这是我们熟悉的欧几里得几何，勾股定理就是平面的度规：$$ds^2=dx^2+dy^2$$
- 球面：单位球面上一小段斜边长的平方不是经度（$\phi$）的平方加纬度（$\theta$）的平方，而是：$$ds^2 = d\theta^2+\sin^2\theta d\phi^2$$
- 平直时空：时间方向长度的平方是负的(取光速$c=1$，下同)：$$ds^2=dx^2+dy^2+dz^2-dt^2$$
度规具体能说明什么信息呢？有了度规我们能计算出某个向量的长度平方的正负，如果大于0，说明该方向类空，即纯空间方向，小于零则类时，即时间方向（有质量的物体的时空轨迹都类时），等于0则是光子的轨迹。时空轨迹的标准术语叫世界线。当引力把时空弯曲后，物体不受外力时也会因为弯曲效应而不得不偏离直线运动。这种特殊的轨迹（世界线）叫做测地线。测地线可理解为弯曲空间中直得不能再直的曲线了。比如球面上的测地线就是过球心的大圆。
探究黑洞内部
要想真正理解黑洞内部的时空，就必须得理解里面的度规。放心我们不会真正介绍相关的运算，只是简单看下施瓦西时空度规的表达式(取光速$c=1$、引力常数$G=1$，下同)：$$f(r)=1-{2M\over r}$$$$ds^2=-f(r)dt^2+ f(r)^{-1} dr^2 + r^2(d\theta^2+\sin^2\theta d\phi^2)$$施瓦西度规，前两项反映了时间$t$流逝跟半径$r$的关系，即反映了径向上的时空扭曲，后面$r^2$项则是正常的半径为$r$的球面的度规，可见球面方向上没有任何扭曲。其中有两个地方很奇怪：一是$r$位于分母，$r=0$时会导致无穷发散，二是当$r=2M$时，$dt^2$和$dr^2$前面的系数也会变成0和无穷大。如果我们先忽略时间，只计算黑洞周围的空间曲率，然后再压缩一维空间维，就会发现它跟下面的这种在科普书中描述黑洞周围时空形状的曲面的内曲率一致：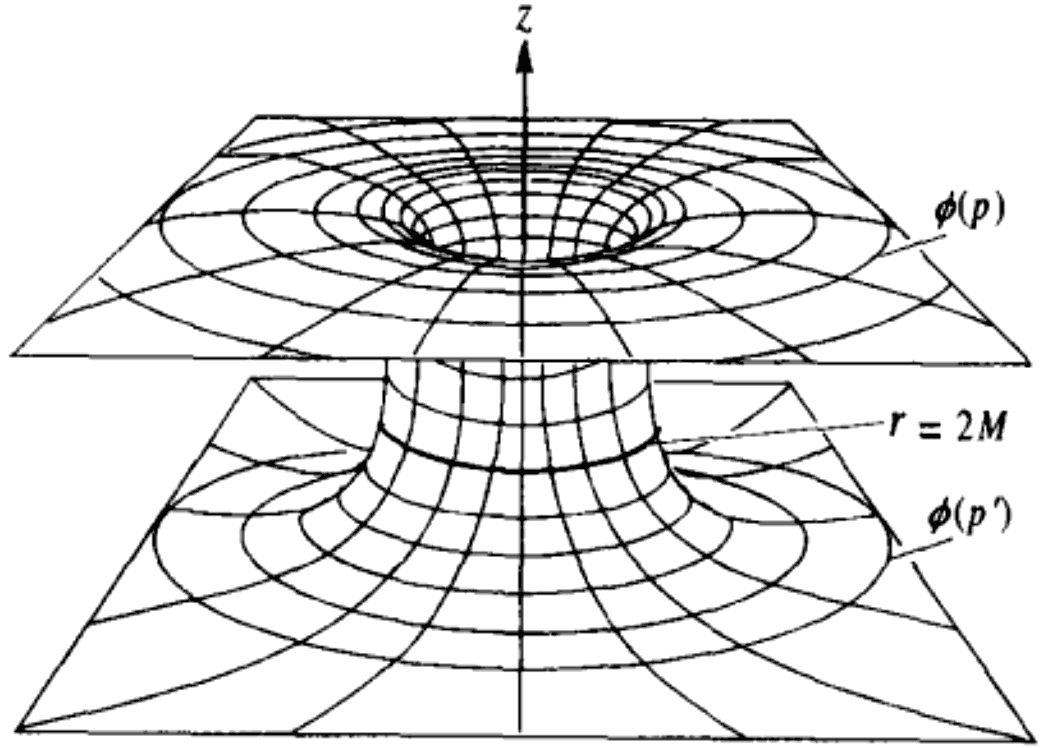
这里的最细的“喉部”的半径就是$r=2M$的地方，似乎我们不能向黑洞内部前进了，然而事实并不是这样的。通过合适的坐标变换，可以找到一套坐标系覆盖整个包括$r=2M$的黑洞内外的时空，除了$r=0$。我们说$r=2M$的地方只是坐标奇性。
你可能会问：明明刚才的图中$r<2M$的区域是个空洞，怎么能通过坐标变换凭空变进去呢？答案是：刚才的图形我们忽略了时间坐标。当加入时间坐标后是可以进去的。下面介绍是施瓦西黑洞的最大延拓：Kruskal延拓——通过坐标变换将$(r,t)$变换成$(X,T)$，球面上的$\phi$、$\theta$不动：$$({r\over 2M}-1)e^{r/2M}=X^2-T^2$$$$\tanh(t/4M)=T/X$$不用理会上面复杂的坐标变换，直接看新坐标下的X-T时空图：（我们只画了前两个坐标，球面上的两个角度在此省略了）刚才的像虫洞一样的图形其实就对应X-T时空图中的$X$轴：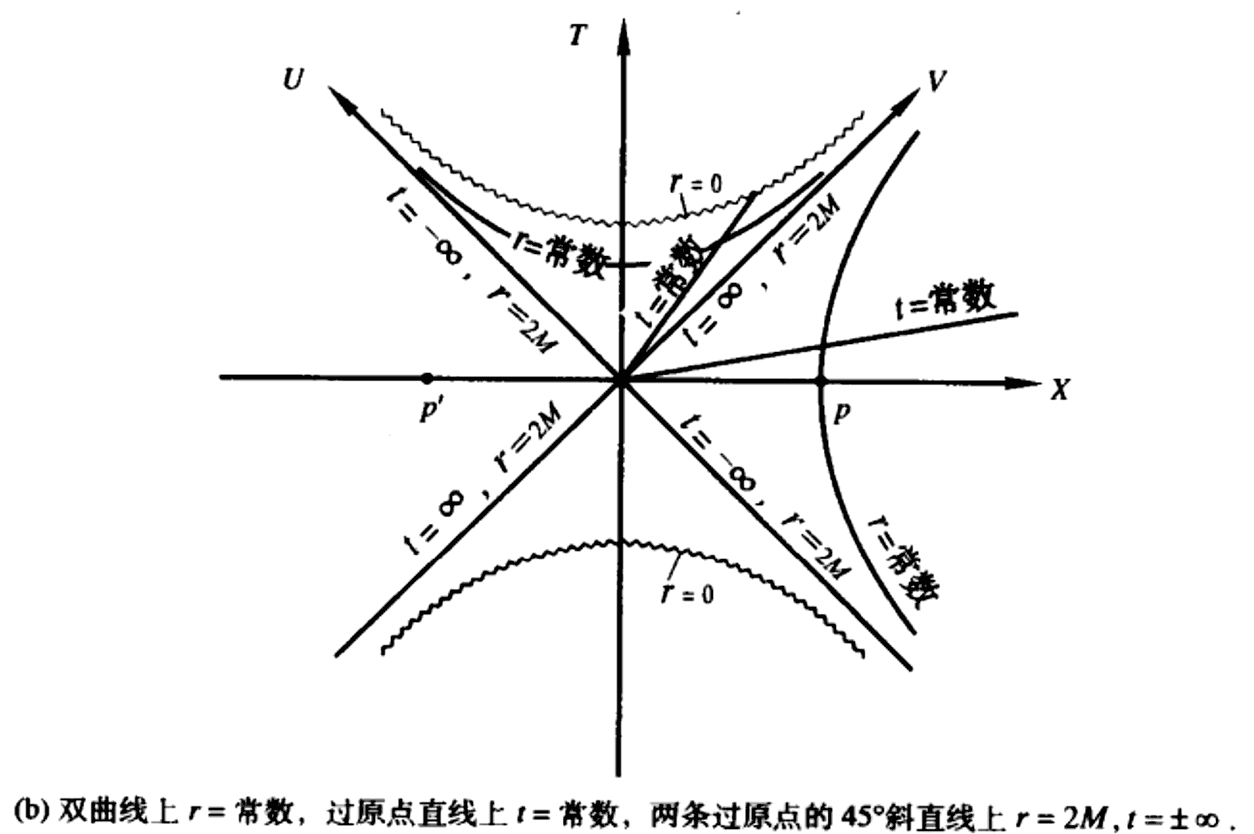
$X$轴上的$r$值的确都是大于等于$2M$的，那个最窄的喉部对应坐标原点。所以这并不是链接两个宇宙的虫洞，因为两边代表了两个没有任何因果联系的宇宙：X-T坐标的一个好处是，45°斜线就是类光测地线，虽然除类光测地线是直线外，其它测地线不一定是直的了，但我们很容易区分光线、类时、类空线。X轴一定是类空的，T轴是类时的。从X轴两边宇宙各自出发的类时世界线，最多只能各自穿过斜着的U/V轴（对应视界）进入同一个黑洞内部会面，不可能在外部的正常时空中会面。注意斜着的U/V轴把时空分成了4个区域，其中T轴负半轴的$r<2M$的那个区域里面$r=0$也是奇点，叫做白洞区：里面的光线只出不进，跟黑洞区是相反的。虽然这里把黑洞白洞上下画在了一起，但跟左右两个宇宙一样，也不存在因果关联，因此没有黑洞一定会有相伴的白洞的说法，这个延拓的时空只代表有数学上的可能性。一般认为白洞违背了热力学定律，是不可能存在的。
我们再来看看具体的时空坐标：原来的时间t参数在X-T坐标中对应一种像双曲角一样的东西，半径r则对应等双曲线的距离（但没正比关系）。为什么说进了黑洞时间跟空间会互换呢？因为当$0 < r < 2M$时，$dt$、$dr$前面的系数的符号正好颠倒过来了。其实这也没那么玄乎：只是我们选取的坐标系不好罢了。这幅图确实表明了$r<2M$后，$r$方向就变到时间方向了。我们可以这样理解空间时间互换：其实并没有规定字母$r$、$t$一定要是半径和时间，它们只不过是特定选择的一套坐标罢了。原来的$t$坐标可认为是无穷远处的观察者看到的时间流逝，由于黑洞内部不再与外界有因果联系，因此理论上可任意选线性独立的任何向量做坐标基底，我们不需要死磕去想时空互换是怎么回事。但是，从另一方面来说$r$方向确实跟半径有关：刚才忽略了的球面上的$\phi$、$\theta$坐标的度规表明，哪怕$r$方向变成类时的了，这个球面的半径也还是r，也就是说，随着沿着r方向的时间流逝，会发现等时面($r$为常数)在不断缩小，直到到了奇点缩小成0。然而奇点在空间方向（原来的$t$坐标，现已类空）上却在无限延伸。其实还有种内向Eddinton坐标能够更直观看到光逃不出黑洞：图中标出了光锥，可见进入黑洞内部，整个光锥都将收缩到$r=0$的奇点。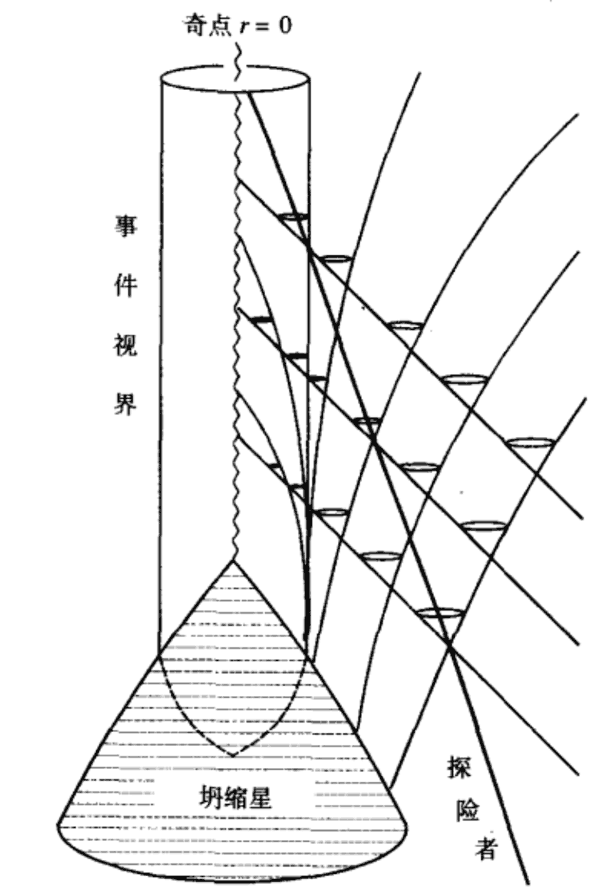
Kerr度规简介
这里介绍旋转黑洞克尔度规的一些性质，为后面的五维旋转黑洞做铺垫。克尔度规表达式有点复杂，这里就不给出了。令克尔度规中的质量M等于0，按理说我们得到的该是平直的时空。但对比平直时空的球坐标表达式能够发现，此时的克尔度规的空间部分并不是三维球坐标的度规表达式，而是一种椭球坐标的度规，准确说叫扁球面坐标系。它可以由二维的椭圆坐标旋转而来。二维的椭圆坐标系由一系列共焦点的椭圆与双曲线组成，其中有个参数$r$可从$0$取到正无穷，等$r$线都是椭圆，即$r$大概对应椭圆的大小，另一个参数$\theta$可取$0$到$2\pi$，类似极坐标。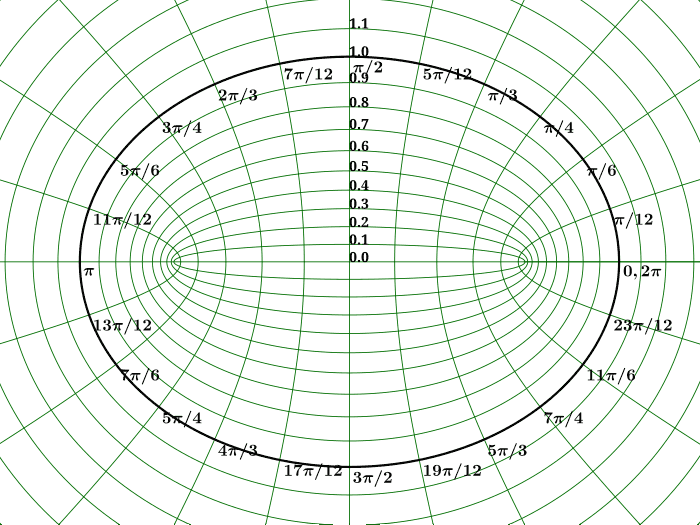
下面我们对椭圆坐标旋转升维：绕椭圆短轴旋转后，就得到了扁球面坐标：引入第三个参数$\phi$表示这个类似于经度的旋转角，原来的$\theta$角现在类似于纬度，可只用在$0$到$\pi$之间取值。原来的双曲线旋转后变成了单叶双曲面。第三个参数$\phi$的坐标面则是绕旋转轴的半平面。此时要注意的是，当$r=0$时，原来的椭圆收缩成了连接两焦点的线段，旋转后则变成了圆盘。Kerr度规计算表明，在有质量的情况下，同时满足$r=0$且$\theta=0$的点的曲率才是无穷大，即焦圆盘的边缘才有奇性，构成了黑洞的奇环。顺便一说：分析度规可知两个视界的形状并不是球面，而是等$r$面，即椭球形的。外面的能层的边界——无限红移面位置的$r$的大小跟$\theta$有关，赤道处$r$最大，转轴处最小，且切于外视界。
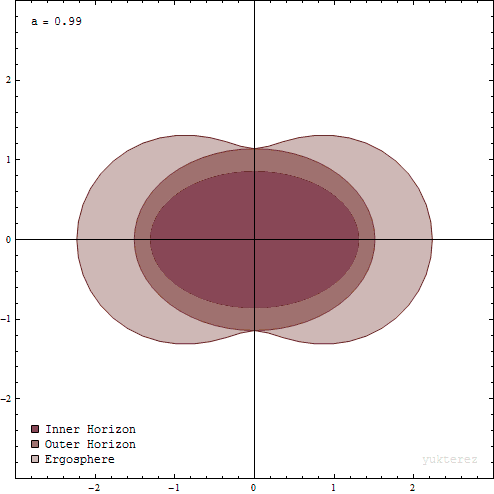
很多Kerr黑洞的结构插图误把$r$理解成了球坐标里的半径，从而把里面的两个视界画成正球面，无限红移面画成椭球，这是错误的。真正的无限红移面的形状在扁球坐标中画出来有点不规则，是类似红细胞那样凹进去的。
(选读) 为了后面能顺利理解五维旋转黑洞和高维的椭球坐标系列，我们来看看各种椭球坐标系：
- 已介绍过的绕椭圆短轴旋转后，得到的扁球面坐标系，具体形式如下（其中$a$为常数，代表焦距）：$$\begin{align} x&=\sqrt{r^2+a^2}\sin{\theta}\cos{\phi} \\ y&=\sqrt{r^2+a^2}\sin{\theta}\sin{\phi} \\ z&=r\cos{\theta}\end{align} $$
- 绕椭圆长轴旋转后，得到了另一种长球面坐标系：与扁球面坐标系不同的是，原来的双曲线变成了双叶双曲面，具体形式如下：$$\begin{align} x&=r\sin{\theta}\cos{\phi} \\ y&=r\sin{\theta}\sin{\phi} \\ z&=\sqrt{r^2+a^2}\cos{\theta}\end{align} $$
- 还有种最一般的三个轴都不相等的椭球面坐标：它的三个坐标面分别是三轴椭球、单叶双曲面和双叶双曲面。椭球面坐标不能靠二维坐标旋转而来，但球坐标系、长球面坐标系与扁球面坐标系都可看作该坐标系的极限形式，详见维基百科。
五维施瓦西黑洞
我们直接给四维时空再加一维空间维就能得到五维时空。当黑洞不旋转时，其结构跟四维的施瓦西黑洞差不多，只是度规中的关于$r$的反比项变成了平方反比，且五维广义相对论在低速近似下是跟牛顿力学相容的，这个文献论证了N维空间中的广义相对论预测星球外部引力的衰减指数跟用通量不变的假设计算得到的是一致的，即在广义相对论的弱场近似下，四维空间物体的引力还是会按三次方反比衰减。
五维施瓦西黑洞的公式还不算复杂，我用WebGPU写了一个光线跟踪的小程序，用于比较四维黑洞与五维黑洞在视觉上的差异。以下图片中，摄像机均位于$r=3$处，吸积盘的内外半径范围为$r=1$到$r=2$之间。我先绘制了施瓦西半径都为0.3时的四维与五维黑洞的情况，发现四维黑洞比五维黑洞看起来要大一些：
我理解为五维的引力衰减得更快，无法控制更远的区域，就显得小一些。下面的对比更明显：我绘制了半径只有0.2的四维黑洞，还是跟半径0.3的五维黑洞比较，发现图中的黑色区域五维比四维的大，但黑洞对光线偏折后吸积盘上半圆的粗细却是四维比五维的大，这或许也是个黑洞外围偏折光线的能力体现。
除此之外，五维黑洞在视觉上并没有比四维黑洞更特别的地方。然而四维空间中是有双旋转的，可想而知，五维黑洞的结构应该会比四维Kerr黑洞更丰富。
注1：五维黑洞理论上是没有稳定的吸积盘的，且星空也非常稀疏，因此“真实”的4+1维宇宙中星星寥寥无几，黑洞周围也是漆黑的，接近隐形。这里为了好看才使用了类似我们宇宙星空的背景（3D/4D星空均由我魔改shadertoy上的Star Nest程序化生成），且加入了球盘形的吸积盘。
注2：这里我采用的是ChatGPT推荐的哈密顿方程来计算四维和五维施瓦西黑洞的光线的弯曲，AI也帮我完成了关键的公式推导。这里有个缺陷：球坐标的极轴附近有坐标奇性，数值不稳定，所以产生的图像会有条瑕疵线，要消除就必须降低步长增加渲染时间，变得非常卡，为了得到一张质量比较高的图片，需要卡10秒左右才能出图，没什么实时交互性。
后来我听CFY说，渲染施瓦西黑洞有个作弊的方法：可以引入“等效势”，把光子当成在类似牛顿力学的中心势场中运动的粒子，跟用微分几何繁琐的计算结果是一样的。于是我们有机会实时体素渲染五维黑洞了！下面是我用Tesserxel引擎渲染的五维黑洞，这个截图中黑洞把黑洞正背面的一颗星的图像扭曲成了一个球壳形升维版爱因斯坦环。这里我添加了更接近“真实”的圆周状吸积盘（忽略了其不稳定性），导致在截面显示中看来黑洞的吸积盘环带只有像棒状的一小截。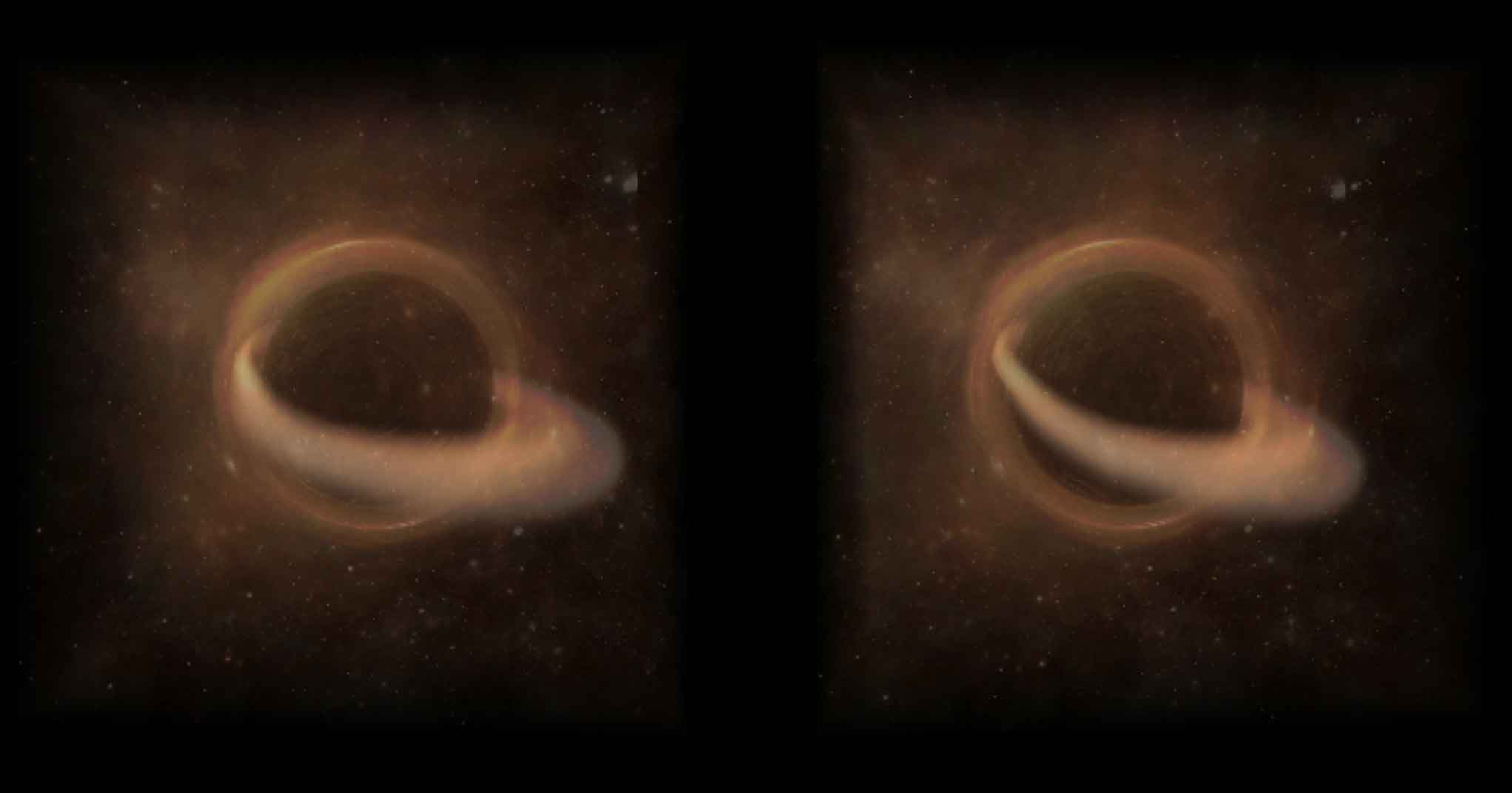
链接在这里，点击右上角Black Hole场景即可。
Myers-Perry黑洞
四维Kerr旋转黑洞解可以类比到任意n维，这种旋转黑洞解叫做Myers-Perry黑洞度规，这里有论文链接。下面我们着重来看看五维旋转黑洞的结构。
我最先没有仔细看那个论文，但可初步猜测单旋转的情况跟四维Kerr黑洞应该也会很像，就是外面有能层/静界，中间有内外视界，最里面有个顺着旋转方向的一维的奇环。双旋转下的黑洞是什么情况呢？其中最特殊的等角双旋转情况呢？
从单旋转黑洞出发，如果此时在其绝对垂直的方向上开始慢慢叠加旋转角速度，则黑洞的结构会怎么变呢？我起初做了一些错误的猜测，有兴趣的读者可以点此处展开查看我的思路。
要真正分析清这个问题，我们应该像Kerr黑洞那样分析出Myers-Perry黑洞度规中质量为0时的平直坐标系是什么样的。计算验证可以发现，给定跟两个角动量大小相关的尺寸参数$a$、$b$后，Myers-Perry度规其实是平直空间做了如下的坐标变换：$$\begin{align} x&=\sqrt{r^2+a^2}\sin{\theta}\cos{\phi_1} \\ y&=\sqrt{r^2+a^2}\sin{\theta}\sin{\phi_1} \\ z&=\sqrt{r^2+b^2}\cos{\theta}\cos{\phi_2}\\ w&=\sqrt{r^2+b^2}\cos{\theta}\sin{\phi_2}\end{align} $$很明显$r=0$时对应着四轴分别为$a$、$a$、$b$、$b$的超椭球面。只要$r$不取0，则前面的系数都更大，说明这种超椭球坐标只覆盖了$r=0$的四轴超椭球外部。这暗示了我们选取的坐标不太好：虽然$r^2$不能为负，但没任何理由限制我们做变量代换$\rho=r^2$，让$\rho<0$，进而可以表示超椭球内部的所有点。$\rho$最小能取到多小呢？可以想象这些共焦超椭球可继续向里缩小，直到短轴缩成0：不妨设$a<b$，则$\rho=-a^2$时，$x$、$y$坐标就缩成了一点不能再缩了（不然$\sqrt{r^2+a^2}$要变成虚数了），整个曲面变成了$zw$坐标面上的半径为$\sqrt{b^2-a^2}$的实心圆盘。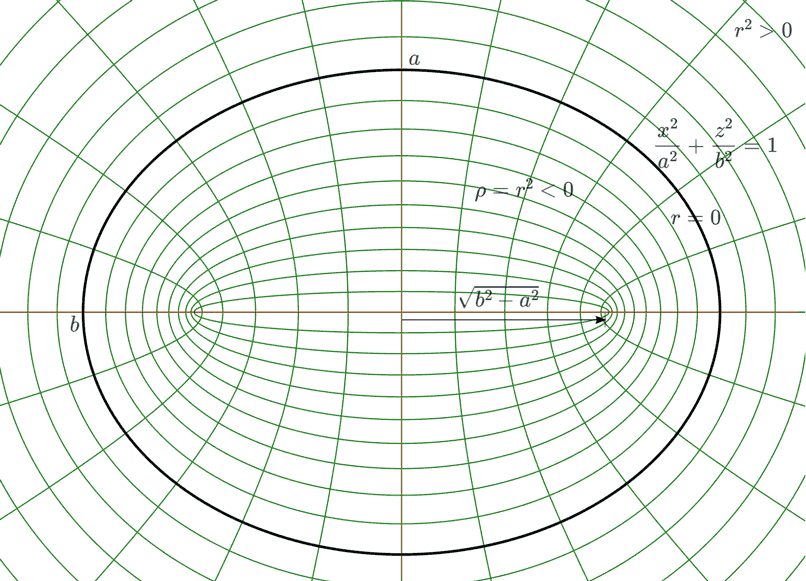
可以证明，Myers-Perry黑洞度规中质量不为0时，只要参数$a$、$b$不同时为0，则在整个$r=0$的坐标面上虽然某些度规的项的系数发散，但曲率都是有限值，没有奇性，说明了刚才我们将$r^2$的值延拓到负数在有质量时也是对的。然而延拓到$\rho=-a^2$时计算发现半径为$\sqrt{b^2-a^2}$的实心圆盘上只有边缘才有奇性，因此也是奇环。
MP黑洞照片
我使用的是CFY推荐的类似直角坐标系的Kerr-Schild坐标计算MP黑洞。然而这种坐标系下光线完全无法进入前面分析的$r^2<0$的区域，这会让GPU计算负数的平方根，直接炸成NaN（不是合法的数值），会强行渲染成黑色。
黑洞转速较小时看起来跟四维Kerr黑洞区别不大：吸积盘一边宽一点，另一遍窄一点，旋转打破了两边的对称性。
你可能会觉得这两边的宽度差别不太明显，其实我只要再调大一点转速，黑色的需要坐标延拓的区域就会从视界中冲出来：可以看到，左侧伸出了一块黑色区域，周围的星光没有沿着边界方向扭曲，说明这里是硬生生被抠去的。不过还有一点跟Kerr黑洞也不同，那就是左边的圆盘环带出现了断裂，这跟Kerr的情况不太一样，这里对光线是否落入视界的判断也有问题，没准已经是裸奇性了，也不知道是不是我的计算有误。
至于传统四维Kerr黑洞的模拟，我推荐这个网站（建议把浏览器窗口弄小一点，不然有直接卡死机的风险）。
虫洞结构？
之前说过$r=0$处可以把共焦超椭球面继续向内收缩成一个圆盘，论文中指出这种收缩还可以再向内部进行，因为计算表明，继续延拓经过的大多数区域的曲率都是有限的，即不会存在奇性阻碍你穿过去，然而这里有些拓扑上的问题。为了能够说清楚，我们先看看四维的Kerr黑洞的虫洞结构是怎么回事。
Kerr黑洞的黑洞区/白洞区的连接结构其实不是令$r^2<0$得到的，而是选取$r<0$(还是满足$r^2>0$)的另一支。为什么科学家会认为穿过这个环会到达新的世界呢？因为计算Kerr黑洞处轴向坐标对$r$坐标的导数，会发现在环面上不为0，按照对称性，向上跟向下接近环面就会产生相反的导数梯度，如果直接认为两侧空间连通，空间在此会形成一个尖角，我们不妨直接从尖角出发把两边各自延长出去，就构造出了另一边的白洞区域——那边是个负质量的、没有视界的、有裸奇性的时空。到了4+1维情况又不同了。我们没法再对圆周内部的空间进行延拓了，这种尖角很可能无法消除。之前我们分析过空间的单连通性，它让我们不管采用什么方式延拓都会有拓扑上的阻碍：要把两块$n$维流形粘在一起，它们的“接缝”的边界一定都得是$n-1$维的，否则在“接缝”处不再是流形。如果不好理解可以先想想一个二维情形：想象一个建立了极坐标的二维平面空间，它可以通过从$r>0$向原点r=0靠近然后进入$r<0$的全新区域，整个空间在拓扑上变成了像一个双锥面的东西。说它是锥也不确切：整个平面没有任何曲率，绕极点一周也还是360°，因此它可以看作压得无限扁、几乎接近平面的双锥。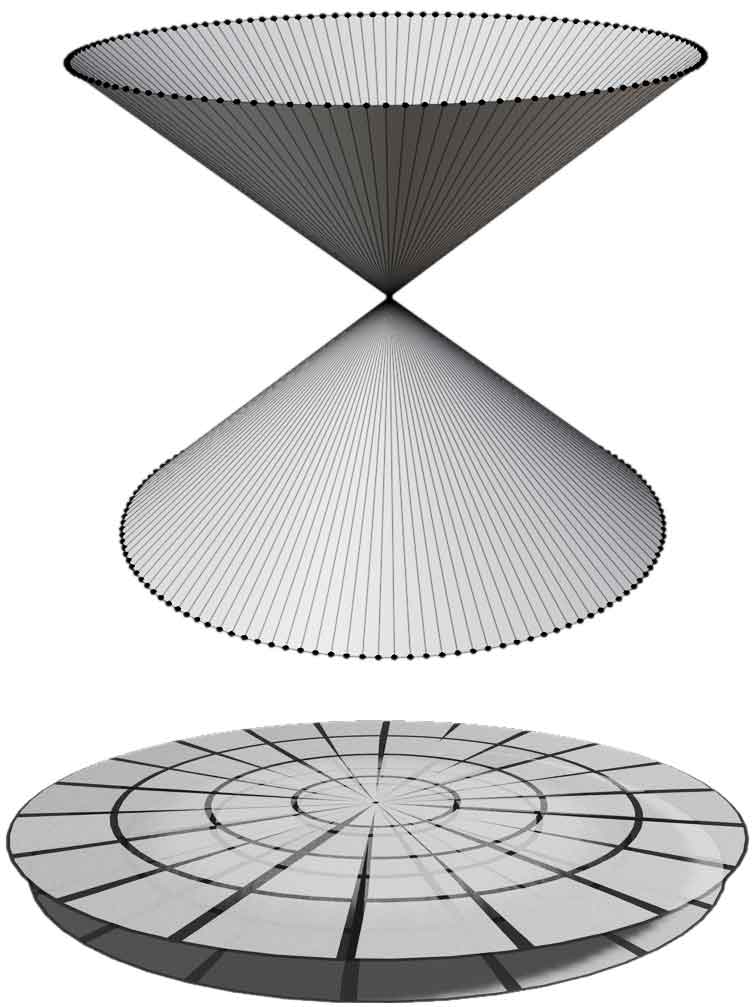
然而除了质点，任何一个有大小的物体都无法通过极点完全到达另一边$r<0$的宇宙：其实没有任何物体能过去，除非它的基本粒子精准不差通过原点，这在量子不确定性中完全不可能。注意整个空间，包括极点处的曲率都是0，也就是说虽然没有曲率发散等奇性障碍，但有空间拓扑上的障碍让这个延拓变得不可能。
以上的例子说明了二维的物体不能穿过点状的传送门，必须要的有宽度的一维传送门才能支持二维物体通过。同理，三维物体无法整个穿过无限细的一根线段，传送门必须要有二维的面积；同理四维物体则需要穿过至少三维的传送门。
论文里说到，对于奇数维时空（偶数维空间）中的旋转黑洞，如果有一个旋转平面是静止的，那个剩下垂直的子空间中会出现一个超球，且曲率奇性只在边缘，但超球内部会存在着弱于曲率奇性的“锥形奇性”（conical singularity），也就是那种尖角情况。我们这里说的情况是平直时空，当加上质量项后，那个锥形不再扁平，就算不延拓我们也会发现锥点周围的时空绕一圈的角度不再是360°，时空流形在此变成了性质不良好的“轨形”（Orbifold）。之前也提到过这种现象在传统的四维Kerr黑洞中也有，只不过Kerr黑洞的奇环圆盘两侧的三维空间在这里像是二胞角，只要让胞继续延伸（即延拓出虫洞），奇性就消失了。可惜这篇论文里完全没有分析过更一般的情况——即所有旋转平面上角动量都不为0时延拓后空间的非流形性，只是机械地分析坐标取到多少后曲率会不会发散。我倾向于认为就像极坐标系的延拓一样，Myers-Perry黑洞最多只能延拓到$\rho=-a^2$的地方，中间的二维圆盘区域的三维体积为0，无法再继续支持有四维体积的任何物体完全穿过它前进至可能的虫洞中去，但是有质量项的MP黑洞的度规不再是平直空间，这里的时空结构是什么样的还需进一步分析，不排除进入黑洞的可能。比如另一篇论文中还画出了黑洞内部的奇性形状，但他的这种坐标系对应质量为零时把平直时空坐标原点强行撑破出一个空洞，然后在这个洞里面填东西，虽然平直的时候是不可能的，但说不定在有质量的弯曲时空中就变得真的有意义了。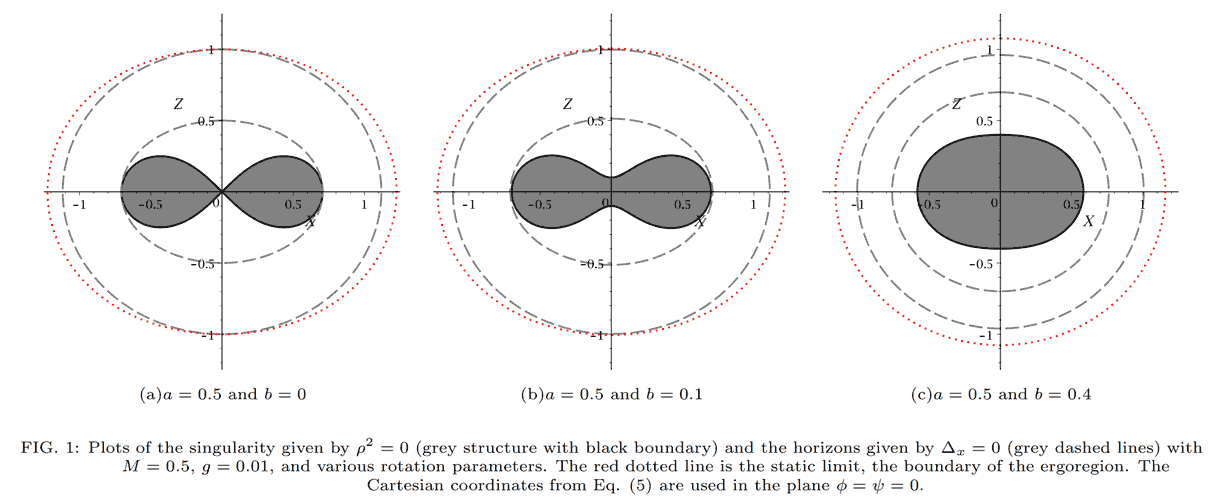
我也问了这方面专业的CFY，他说按理说能否延拓只用看是否有曲率发散的障碍，但这样延拓出来的东西肯定不是虫洞了，他也不知道会得到的是什么，如果大家有不同看法欢迎留言讨论。
小结
现在我们终于可以描述五维Myers-Perry度规的任意双旋转黑洞的奇性了：
- 当黑洞单旋转时，类似Kerr黑洞，奇性是一个圆盘，其边缘有着曲率奇性，内部则是锥形奇性，它被包裹在内外两层视界之中，且无限红移面在转轴处切于外视界。
- 当另一个绝对垂直的平面上也开始增加角动量时，奇环会慢慢缩小，在转轴处的无限红移面也会慢慢脱离外视界，没有地方相切。奇环在四维空间里面是撑不开虫洞的，四维生物要进行虫洞旅行不能靠黑洞，还得想其它更复杂的方法。
- 等角双旋转时奇环退化成奇点。之前说的任何拓扑突变都不会发生，整个黑洞由从外到内三层超球面构成：无限红移面、外视界、内视界，奇点位于超球心。
高维MP黑洞结构
在高维时空中，要想在旋转黑洞内部撑开虫洞，就必须让奇点的维度比较大，破坏时空的单连通性。奇性的形状来源于旋转速度的不均匀性：看似Myers-Perry度规的奇性是个正比于各点角速度的超椭球面，然而只要该超椭球面可以做“共焦收缩”，它都可以继续通过收缩向内部延拓，直到碰到超椭球的某些轴的长度变成0才遇到真正的曲率奇性。比如不旋转的黑洞和完全对称的双旋转黑洞的任何地方的线速度都相同，它们的奇性都是一个点，只有角速度不同的双旋转或单旋转才会将奇性撕裂成一个环状。在六维时空（五维空间世界）中，我们可以构造一个双旋转黑洞，但其在第五维上存在一根没参与旋转的轴，可想而知，这个星球的奇性位于垂直于该轴的四维子空间中，根据双旋转是否等角，奇性可能为正超球面或椭超球面。挖去这个超球面，五维空间不再单连通，我们可以在第五维垂直的方向上穿过去，没准可以从白洞出来到达一片新的宇宙。下面我列了一张表总结一下前几个维度的MP黑洞结构。这里我暂时认为对空间单连通的共焦圆周再进行延拓都有锥形奇性，并对这些拿不准的情况标注了问号（很可能还可以继续向内延拓一段距离，但不会有虫洞），若有不同看法欢迎指出：
| 旋转类型 | 4维情况 | 5维情况 | 6维情况 | 7维情况 | 8维情况 |
|---|---|---|---|---|---|
| 单旋转 | S1曲率奇性，有虫洞 | S1曲率奇性，D2锥奇性，无虫洞 | D2曲率奇性，无虫洞 | D2曲率奇性，无虫洞 | D2曲率奇性，无虫洞 |
| 双旋转 | - | S1曲率奇性，D2锥奇性？无虫洞 | S3曲率奇性，有虫洞 | S3曲率奇性，D4锥奇性，无虫洞 | D4曲率奇性，无虫洞 |
| 等角双旋转 | - | 点状奇性，无虫洞 | S3曲率奇性，有虫洞 | S3曲率奇性，D4锥奇性，无虫洞 | D4曲率奇性，无虫洞 |
| 三旋转 | - | - | - | S3曲率奇性，D4锥奇性？无虫洞 | S5曲率奇性，有虫洞 |
| 三旋转/$a=b$ $<c$ | - | - | - | D2曲率奇性，无虫洞 | S5曲率奇性，有虫洞 |
| 三旋转/$a=b$ $>c$ | - | - | - | S3曲率奇性，D4锥奇性？无虫洞 | S5曲率奇性，有虫洞 |
| 等角三旋转 | - | - | - | 点状奇性，无虫洞 | S5曲率奇性，有虫洞 |
新天体：黑环
通过研究解爱因斯坦方程可发现，五维时空中还存在着一种不同于Myers-Perry度规，叫做“黑环”(Black Ring)的黑洞解。它的视界是球环的表面（$\mathbb{S}^1\times\mathbb{S}^2$），由于黑环的形状中间是空的，会自发在引力作用下坍缩。要让黑环稳定，就必须要让它转起来，在离心力的作用下保持平衡。因此黑环的角动量、质量、半径、胖瘦参数会有个约束关系。值得一提的是，在某些条件下，黑环可以跟刚才介绍的MP黑洞拥有相同的参数，这意味着我们找到了黑洞无毛定理的反例：黑洞无毛定理仅在四维时空中成立，在五维及更高情况下它失效了！
理解黑环的度规表达式就更难了。下面我只大概挑些结论罗列出来：
- 黑环视界的拓扑结构是球环面，MP黑洞视界的拓扑则是超球面（超椭球跟正超球在拓扑上是一样的哦）
- 黑环的结构其实类似于直接把四维时空（就是我们宇宙）中的施瓦西黑洞在第五维上柱化得到的“黑弦”（Black String），然后再把黑弦弯曲成环形。
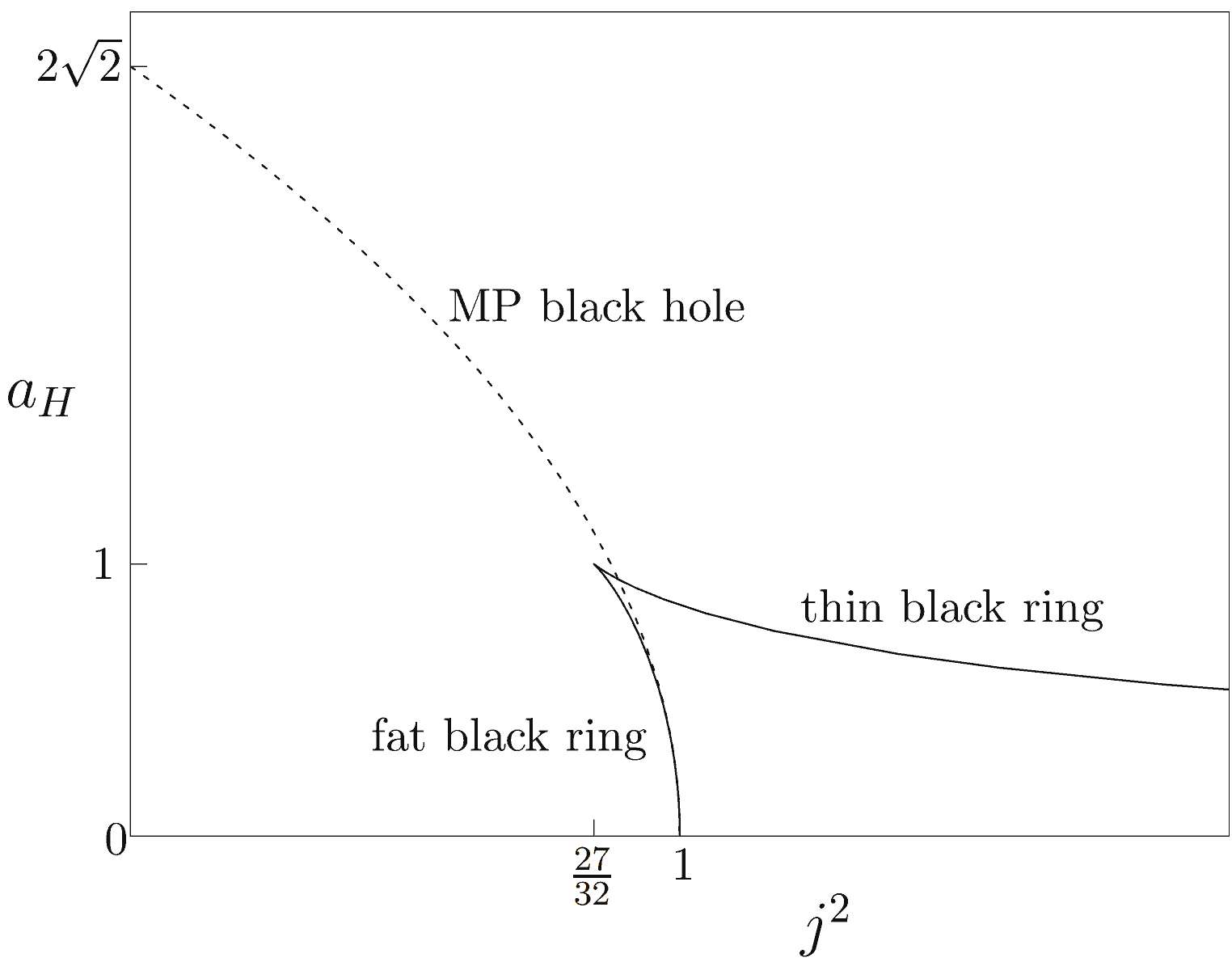
- 同一参数下，除了可能有MP黑洞解，黑环自身也可能有两组解，一组叫瘦黑环，一组叫胖黑环。如下图中角动量参数$j^2$取${27\over 32}$至$1$之间时共有三种解。
- 黑环也可以有双旋转解：一个方向是绕$\mathbb{S}^1$的方向，另一个是绝对垂直的在$\mathbb{S}^2$中的旋转方向。可能你会直观想成那种烟圈的从里向外翻的非刚性旋转，但球环的双旋转完全是刚性的，不会像烟圈那样里外翻。
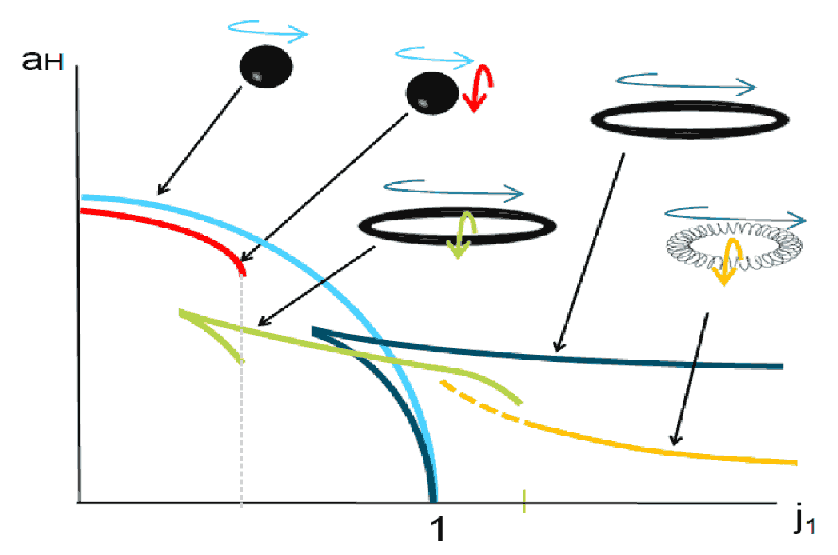
- 还存在一个黑洞加一个黑环的类似于“黑土星”（下图(d)）的结构，以及多层黑环等更复杂的嵌套结构。
- 对于高维黑洞，其稳定性可能会随着角动量参数的增大而“分叉”，变成更复杂的形状，这跟旋转星球的形状的稳定性有些类似。
黑环的可视化
MP黑洞与黑环的可视化早就有人研究过了。我找到了一篇论文，作者把球环的两个典型截面拉了出来：一种是两个球，另一种是一个圆环。论文作者指出，单看截出两个球的黑环渲染截面会发现跟传统四维时空中的包含两个黑洞的时空看起来非常像，比如如果从视线方向看过去，一个黑洞在另一个黑洞正后方时，其黑洞阴影会被扭曲成一个环形。垂直与两黑洞连线方向看过去时，由于光线可以在两边黑洞周围绕圈，会导致黑洞两侧有着像眉毛那样的对方黑洞阴影的扭曲像。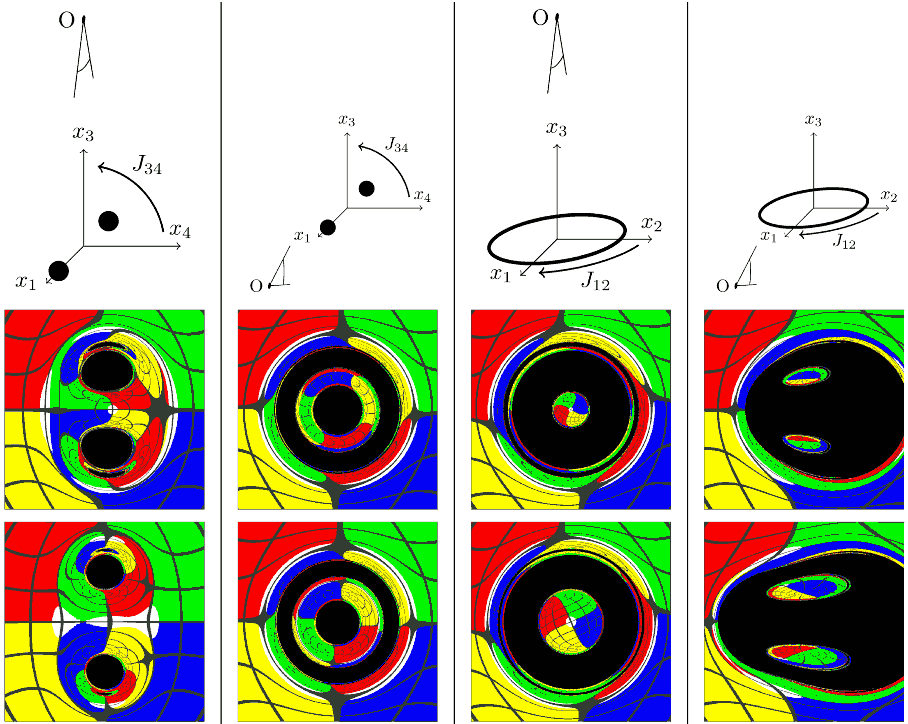
黑环的度规表达式太复杂了，我直接放弃了自己计算的想法。不过之前施瓦西黑洞的等效势提醒我，或许可以建立一个带电圆环的电场势模型来直接扭曲光线，看看能不能得到跟上面论文中相似的图像。结果我得到的图像跟论文里的黑环真的非常像！除了有一点：黑环旋转的两个方向上的光线本来该有像Kerr黑洞那样的不对称，导致黑环一边粗一边细，我的带电圆环则只能模拟静态的吸引力，无法模拟旋转带来的参考系拖拽效应，两头都是一样粗的。我试着在模型中加入了磁场项，把光子看成带电粒子，加上了在磁场中受洛伦兹力偏转的贡献，发现无论是Kerr黑洞还是黑环都完全跟真实情况不像，于是我只能放弃了加旋转。不过，这些静止的伪黑环看起来还挺漂亮的。（注：我没有在黑环周围添加任何吸积盘，链接在这里，点击右上角Black Ring
）
下面是一些特定角度的体素截面照片，可以看出确实跟论文里的黑环图像很像：
此外，我还抓取到了圆环的一个经典双圆截面的类似有趣的黑东西：
黑环才是太阳？
最后我想单独提的一点是，人们已经论证过，MP旋转黑洞周围也不会存在稳定的行星轨道，而黑环可能才是四维文明所在行星的“太阳”的唯一候选者，因为这篇论文指出，黑环周围有可能拥有稳定的轨道，且黑环时空本身在微扰下也是稳定的。我是这样理解的：姑且忽略相对论的部分，远处看来黑环就是普通的四维恒星，行星要么坠落要么逃逸，但当行星靠近后“放大看”坠落的行星不是直接撞了上去，而是穿过了中间的洞；近处看来，黑环的线状质量周围的场相当于普通三维空间中点状质量周围的场近似“柱化”升维得到，有稳定的轨道也就显得不足为怪了。这里我也在Tesserxel中对环状的天体周围的行星轨道进行了非相对论的模拟（使用RK4积分器），发现确实是有稳定的轨道！如果太阳是环形的，之前介绍的行星上的日期、历法、季节全都会变完，但行星一会在太阳环外侧一会又钻进太阳环内侧，气温变化跨度可能非常大，行星的轨道能否完全落在星系的宜居带内可能是件困难的事情。
参考文献
- arXiv:1111.1903 [gr-qc] Myers-Perry black holes MP黑洞度规与结构介绍。
- arXiv:1711.02933 [gr-qc] Geodesic motion in the five-dimensional Myers-Perry-AdS spacetime 主要讲负常曲率时空中的MP黑洞，里面绘制了MP黑洞向$r^2<-a^2$内部继续延拓的奇性。
- arXiv:1903.05125 [hep-th] Imaging Higher Dimensional Black Objects 绘制了MP黑洞与黑环的体素图像的截面。
- arXiv:2411.02511 [gr-qc] Darkness cannot bind them: a no-bound theorem for d=5 Myers-Perry null & timelike geodesics 分析了MP旋转黑洞周围类时与类光轨道稳定性。
- arXiv:1302.0291 [hep-th] Stable Bound Orbits of Massless Particles around a Black Ring 黑环周围可以拥有有界的类时和类光测地线，即稳定轨道。