四维世界(六):牛顿力学
这个系列一直都在设想一个虚构的四维世界。无论我们怎样用语言描述它的样子,缺乏物理学的世界都是静态的不能交互的。所以今天我们来学习一下这个世界里的牛顿力学。这个世界的构建理念就是要尽可能接近我们的真实世界,只是在维度上不同,所以我们全盘照搬三维世界中的理论就行了。仿照三维的游戏物理引擎我们也能写一个四维物理引擎。比如Marc ten Bosch的4D Toys就相当不错,但游戏里只能固定移动截胞(2024更新:貌似后面作者加入了旋转截面功能),且不能自定义场景,所以我又自己造轮子写了一个。
先睹为快
如果你还不知道什么是3D视野的话,请先看教程再回来哦:
这里有很多四维物理场景(以后可能还会增加),你可以自由旋转角度观察场景。但遗憾的是除了可以按鼠标右键发射超球炮弹之外,我没想出更好的与物体交互的方法。(最好看后面的讲解获得更好的体验哦)
|

|

|

|
| 
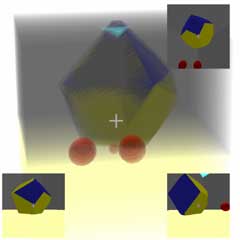
四维齿轮(控制面板可调转速) |
四维汽车
操作方法
使用W S前进后退,J L I K 左右、侧前侧后转向,U O自转。相机固定在车上,按大键盘1 2 3可以在三个视角上切换。
解释说明
这是一个有着8个双圆柱轮子的超长方体后驱小车。物理引擎中直接给四个后轮施加转矩,转弯时对前轮施加转矩。汽车都靠物理引擎计算摩擦力自然前进或转向。这个四维汽车主要是为了验证文章《四维世界(二):公路交通》中对四维车的构想。建议与此文章一起食用。
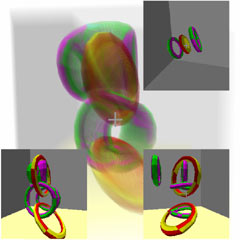
四维陀螺
我们在文章《四维空间(八):参观四维国》中提到过不同物体的滚动,下面我们就来看各种球体、柱体、锥体的滚动,锥体倒过来能否当成陀螺,稳定性如何。这里来就不从数学上证明了,我们直接像做实验一样(或玩玩具一样)来得出定性结论。通过右边的控制栏来切换不同的场景。可以点击鼠标右键发射超球与物体交互。(注意发射太多会使场景解算变慢,严重时会降低解算精度导致穿模,物理引擎太难优化了。。)
滚动
这里列出了常见四维物体在三维地面上的滚动:(没说自由度的默认为1)
- 超球:可以任意滚动;(自由度:3)
- 球柱:平放可以在垂直母线方向上移动(自由度:2)
- 圆柱柱与双圆柱:均只能朝一个方向滚,且圆柱柱必须横放与地面,但双圆柱底面与侧面都是圆,横竖没区别,都能滚动。
- 圆锥锥:横放在地面时(注意底胞与地面有倾斜夹角,下同)与地面接触图形为三角形,其中有两个顶点是两个锥角,另一个顶点是立起来的圆与地面的切点。圆锥锥在三维地面中可以绕着两个锥角确定的轴打转,就好比三维的圆锥滚动时绕着顶点转圈一样。
- 圆锥柱:与圆锥锥类似。横放在地面时与地面接触图形为矩形,一组平行边为柱体母线方向,另一组为圆锥底胞与地面的切线。可绕着过锥角的柱体母线方向作为轴旋转,也就是说柱体方向不变,感觉完全是圆锥底胞在垂直于母线方向的三维空间内滚动。
- 球锥:与三维地面切于一条线段,其中一端为锥角,另一端为球胞与地面的切点。可饶锥角自由旋转。(自由度:2)
- 双圆锥:与三维地面切于一条线段。线段的两端点对应两个绝对垂直的圆与地面的切点。两个圆在切点处的切线与线段三者互相垂直。双圆锥可以绕任意一个端点并以此端点圆切线为轴旋转,此时另个一端点向着那个端点的切线方向前进。但绝对垂直旋转的不相干性可以让两端的旋转互不干扰,也就是存在每个端点都朝自己切线方向的双滚动。双圆锥的旋转可以说是最奇怪也最不好理解的了,因为我们没有任何三维空间中的相似经验。
陀螺
- 圆锥锥:把两个锥角放到地面上,在圆的平面内转动。这个陀螺具有稳定性:陀螺的角动量守恒保证了圆所在的旋转平面不会倾斜,而与之绝对垂直的旋转方向上角动量为零,但两个锥角放到地面上阻碍了这个方向上转动。
- 圆锥柱:把锥线(过圆锥锥角的母线)放到地上,圆柱胞翻过来平行于地面,在圆的平面内转动。相当于直接把三维的圆锥场景整个柱化。与圆锥锥类似,旋转起来后锥线放在地上阻碍转动,也具有稳定性。
- 球锥:锥点朝下放在地面上,把球胞翻过来朝上平行于地面。旋转可以是球胞内任意的简单旋转(即旋转平行于地面)。但球锥陀螺没有稳定性,因为有平行于地面的一个方向上有角动量,会保持这个平面不会倾斜,但与这个平面垂直的平面可以转动,即球胞内旋转的转轴可以网竖直方向旋转,这个方向上的一点扰动就会让陀螺直接倒下。有意思的是,就算陀螺倒了也不会乱滚,因为平行于地面的方向上的那个角动量会继续维持旋转稳定,也就是说陀螺倒下后还会继续旋转,与地面接触与一条线,这条线连接着球胞的转轴,线上的点都是不动的,所以不会乱滚。
- 双圆锥:让一个圆平行于地面,另一个垂直地放在地上。在平行于地面的圆所在平面内旋转。由于垂直地放在地上的圆所在平面没有角动量,稍微有点扰动这个圆都会倒下,所以没有稳定性。如果是双旋转的话双圆锥上就找不到不动点,垂直方向上的圆会充当轮子使双圆锥滚走。
- 圆柱锥:跟之前的锥体一样,在垂直于旋转方向上没有稳定性,且地面上只有一个锥点,不像圆锥锥与圆锥柱那样有支撑,所以易倾倒,不稳定。
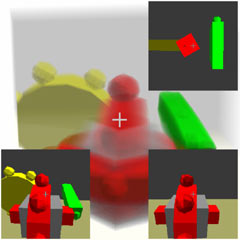
四维齿轮
操作方法
展开右边控制面板,可以调节转矩参数来控制齿轮马达的转速。
解释说明
四维齿轮一是一个绝对垂直齿轮传动机构。可以控制绿色齿轮的转速来驱动绝对垂直的黄色齿轮。绝对垂直齿轮传动的原理是通过两次半平行半垂直齿轮传动实现的。
四维齿轮二是一个双旋转合成器。其中色齿轮是两个绝对垂直的单片齿轮连在一起的,它可以分别被不同垂直方向上的齿轮带动且不相互干扰。
四维锁链
点击右键可以发射超球与物体交互。(别发射太多啦,会崩。。)
里面具体几何体如何串起来请参考这篇文章:《四维空间(十):扭结与环扣》。
刚体力学
四维空间中的平动性质其实跟三维区别不大,我们这里主要关注与旋转相关的内容。
旋转的表示
下面我们来谈谈背后的物理公式。四维空间中的质点的位置向量用四个坐标表示:$(x,y,z,w)$,速度就是坐标对时间求导,也是个四维向量$(v_x,v_y,v_z,v_w)$,加速度同理,所以牛顿三定律在四维是没有任何问题的。但对于刚体力学,我们除了要计算物体的位置、速度、加速度,好需要计算物体的朝向、角速度甚至角加速度。四维空间的旋转跟三维差别还是挺大的。表示物体的朝向就是表示一个特定的旋转。表示旋转的方法有很多,如:
- $4\times 4$正交矩阵
$$Ox=\left(\begin{matrix} a & b & c & d \\ e & f & g & h \\ i & j & k & l \\ m & n & o & p\end{matrix}\right)\left(\begin{matrix} x \\ y\\ z\\ w \end{matrix}\right)$$ - 欧拉角的四维类比:使用一些固定平面上的固定先后顺序的复合旋转来表示任意旋转。(可能会出现Gimble Lock等不好的现象)
- 几何代数中的旋量
$$RxR^\dagger$$
其中$R = (a+be_{xy}+ce_{xz}+de_{xw}+ee_{yz}+fe_{yw}+ge_{xw}+he_{xyzw})$,$x=(xe_x+ye_y+ze_z+we_w)$,$R^\dagger=(a-be_{xy}-ce_{xz}-de_{xw}-ee_{yz}-fe_{yw}-ge_{xw}+he_{xyzw})$ - 四元数
$$pxq=(a+bi+cj+dk)(x+yi+zj+wk)(e+fi+gj+hk)$$
其中前两个方式是较好理解的,但真正计算的复杂度以及精度可能并不理想,因此一般用后两种方法。这里的细节就不展开了。
角速度
然后就是角速度:角速度到底是什么?它反映的是旋转的方向与速度。在四维,角速度是一个2-向量,这也是我们之前提到过的。知道了角速度$\omega$我们就能够确定刚体上每一点因转动带来的线速度:
$$v = r\cdot \omega = (r \wedge \omega^*)^*$$
注意由于现在的$\omega$表示旋转平面而不是转轴,所以从三维推广过来求线速度本来该用外积但定义变成垂直方向后就变成了内积。举个例子:绕zw平面旋转的单位角速度是$e_{xy}$,$e_x=(1,0,0,0)$处的速度为$e_xe_{xy}=e_y=(0,1,0,0)$,而$e_y=(0,1,0,0)$处的速度为$e_ye_{xy}=e_ye_xe_y=-e_xe_ye_y=-e_x=(-1,0,0,0)$(相同字母像内积那样乘起来得到数,不同字母相乘交换会变号,具体请参阅几何代数相关内容)
转动惯量张量
如果你觉得四维空间的旋转与角速度已经够难以理解了,那么转动惯量才是更恶心的。我们知道质量反映的是力改变物体速度的难易程度:
$$F=ma=mdv/dt$$
转动惯量则反映力矩改变物体角速度的难易程度:
$$M=Id\omega/dt$$
但转动惯量比平动惯性更复杂,它跟空间朝向有关,而且力矩$M$的方向不一定与角速度$\omega$的方向一致,所以一般来说转动惯量$I$是一个矩阵。在三维空间,由于$M,\omega$只有三个自由度$e_{xy},e_{yz},e_{zx}$(等价于垂直的向量$e_{z},e_{x},e_{y}$),所以$I$就是三阶矩阵。注意,盲目将$I$是三阶矩阵类推到四维是四阶矩阵的想法是错的,因为四维中的$M,\omega$是有六个分量的2-向量,转动惯量矩阵$I$是六阶矩阵!如果你把2-向量看成是$4\times 4$的张量的话,转动惯量就是一个有很多重复分量的$4\times 4\times 4\times 4$阶张量。还有一个例子也能说明直接类比不成立:二维空间的转动惯量只需要一个数,并不是二阶矩阵。
好了,四维牛顿刚体力学中与三维不一样的就主要是这些了,有了理论基础就可以写物理引擎了。
物理引擎是如何工作的?
在打算做四维物理引擎之前,我也很好奇。很久前我只做过平面上打台球的小游戏,涉及到刚体旋转、碰撞都是懵的,总不至于一来就写四维吧。我先自己写了一个基于弹力的二维物理引擎,虽然勉强能用,但稳定性很不好。后来我找到了一本书,叫《Game Physics Engine Development》,它非常仔细地从零基础的向量讲起,一步一步教你写一个3D游戏引擎,于是我也依葫芦画瓢,照着直接改成四维版的。(原书用的C++,我改成了Javascript)
物理引擎主要做两件事:物体受力运动与物体碰撞。按理说物体碰撞也是受力,但碰撞过程太快,瞬时力是很大且持续时间短的脉冲形式,计算很不稳定,所以一般单独处理。牛顿第二定理告诉了物体受力怎样运动,计算机通过一些数值算法就能搞定。(我直接用的欧拉法)
碰撞检测
要处理碰撞,首先就要知道两个物体是不是要碰上了,这一步叫碰撞检测。碰撞检测就是一个几何问题,它可以给出两个物体是否相交,若相交则还能给出交点位置、分离方向与距离。这一部不涉及任何物理,但计算繁琐。比如判断两个任意多胞体是否相碰很麻烦,因为有不同的情况要分类讨论。(顶点与胞碰、面与棱碰等)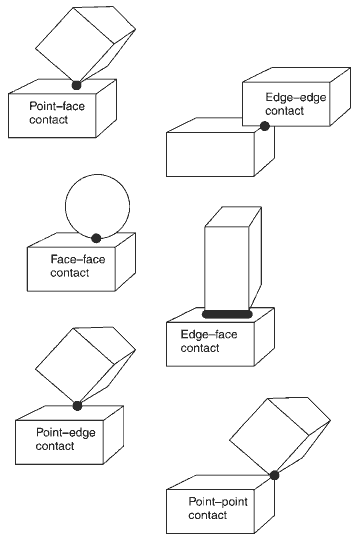
碰撞处理
碰撞处理的方法特别多,这里只简述一下我看的那本书里的方法:如果碰撞检测发现两个物体相交了,引擎需要把物体在分离方向上分开。如果发现两个物体相交并有相互靠近的速度,则把分离方向上两者的相对速度反向来得到弹开的效果。如果是不完全弹性碰撞则反向后还要乘以一个因子。如果不考虑物体转动的话,这样就够了,如果考虑物体转动,角速度与线速度的改变都对分离方向上两者的相对速度改变有贡献,而角速度与线速度的改变都是由一个可以用冲量来表示的大且持续时间短的脉冲力导致的。我们已知的是分离方向上两者的相对速度,所以通过解方程的方法即可反推出冲量的值。得到冲量后我们就能算出具体角速度与线速度因碰撞的改变量了。值得一提的是,对摩擦力的模拟同样也可以通过已知相对速度的方式解方程得到,且可以与碰撞同时求解。
说了这么多,我们只处理了两个物体之间的碰撞。但场景中往往有非常多的物体,比如堆起来的积木等。不同碰撞之间的求解可能是冲突的。简单的方法是根据严重程度先后解决,然后不停迭代,高级的方法是将多个相关联的碰撞求解联立得到更精确的结果。反正我就用的最简单的那种方式,效果也还行。
一个成熟的物理引擎不止我说的这些,这里就不展开介绍约束解算、接触解算、提高精度性能等更多内容了。以这个标准,这个四维物理引擎只能算是可以用而已,需要改进的地方太多了。
