类型论与机器证明简介

上篇文章介绍了命题逻辑、一阶逻辑再到ZFC集合论，本文来看一种新的宣称想要取代集合论在数学中地位的新东西——类型论。事实上它已经广泛运用在机器证明当中，其中最著名的就是四色定理的证明了，同时它跟程序代码很类似。把类型论稍加改造成同伦类型论，它还能比集合论更加“直接”地处理拓扑学中的许多问题。

类型论的动机

“类型”这一概念广泛被用于编程语言中，具体来说用于编译前的类型检查，比如下面这段C语言代码

int i = 0;       // 定义整数变量i，并将其设为0
string j ="oma"; // 定义字符串变量j，并将其设为"oma"
int k = i * j;   // 定义整数变量k，并将其设为 i * j

编译时会报错，因为这段程序声明i是整数类型的变量，而j是字符串类型的变量，它们无法相乘，或者说，乘法运算是一个接受两个数作为输入参数，输出返回一个数的函数，这里输入的i、j的类型显然与之不匹配。从上面的例子可以看出，类型检查其实就是编译器帮助我们检查代码有没有明显的低级错误导致执行一些像把数字与字符串相乘的这种无意义的命令。虽然检查一个表达式的类型也是机械化的（可定义成形式系统），但这似乎跟数学逻辑没有一点关系，它居然能用来构建公理化体系？yugu233做过一期视频《论码农与数学家的相似性【数学地图】》非常通俗形象地解释了类型跟证明之间的联系。

题外话选读:
不知道有没有熟悉typescript(即带类型检查的JavaScript)的读者，它里面的类型推导机制功能很强大，已经达到了图灵完备，只要知道原理就很容易用纯类型推导定义出自然数，并可以进行四则运算，可参考这里。这些计算完全在编译器检查代码时完成，这些代码只包含一堆类型声明，编译出的执行文件是空的。注意这其实跟我们要说的类型论没什么关系。

方便起见，我们将“变量a的类型为A”记作“a : A”。类型论的推理能力主要来源于关于函数的事实: 设A和B为类型，假设存在某个函数f : A → B，则f能实现这个功能：给定一个变量a : A，就能得到一个类型为B的变量f(a) : B。

跟所有形式系统一样，这些函数、变量都只是一些无意义的符号。如果你把它们理解为一段计算机代码，则它们对应着物理上存在内存中的变量和函数跳转等指令。下面我们用一种全新的视角理解它们：把“a : A”翻译成“a见证了命题A为真”。即，把类型翻译成命题，把相应的变量翻译为命题为真的证据。让我们想想下面类型论的规则在新视角下代表什么。

已知“a : A”与“f : A → B”，就能构造出“f(a) : B”

上面这句话在说如果命题A与命题A → B都成立，则能推出命题B成立，等价于命题逻辑的推理规则mp！而且这里函数类型中的箭头符号恰好能解释为推理中的逻辑蕴含箭头符号！而且类型论其实根本不止这点能耐，它不仅能处理命题逻辑，稍加改造就能处理一阶逻辑和更高阶的逻辑，但在这之前让我们再熟悉一下这个形式系统。比如，如何用类型论证明下面的定理呢？

如果命题A → B与命题B → C都成立，则能推出命题A → C成立

类型论中，命题成立代表着这个类型下面一定有某个值存在，叫做该类型是居留（inhabitated）的。于是我们可以假设存在两个函数f与g，有f : A → B, g : B → C 。只要能构造出新的函数h : A → C我们就算证明了原命题。显然函数复合就能实现，定义h(x) = g(f(x))，很容易验证h的类型就是A → C。

可是类型论是个形式系统，目前还没具体给出推理规则，否则能否允许定义h(x) = g(f(x))都不清楚。下面我们就来简单介绍一下类型论的基础——$\lambda$演算。

无类型Lambda演算

Lambda演算有很多种。其中无类型$\lambda$演算是一个所有东西都是函数的形式系统，这跟集合论的那种所有东西都是集合的观点相似。但它不基于一阶逻辑，它有自己的符号构建语法和推理规则：

• 所有合法的字符串都叫“$\lambda$项”，只能使用以下3条规则构造“$\lambda$项”：
  1. 变量是$\lambda$项，一般用小写字母表示，如x、y、z、a、b、c、f、g、h等；
  2. 若x是变量，M是$\lambda$项，则(λx.M)是$\lambda$项，它可以解释为函数f(x)=M；
  3. 若M、N都是$\lambda$项，则(M N)是$\lambda$项，它可以解释为函数作用M(N)。
• $\lambda$项只是一个表达式，并不是一个断言或命题，因此还有一种包含等词的字符串断言两个项相等：
  • 若M、N都是$\lambda$项，则M = N是一个命题
• $\lambda$项的推理规则有三个：
  1. (α-变换) 定义函数时自变量的名称并不重要。比如说λx.x和λy.y是同一个函数。α-变换就是说这两者相等，即(λx.M) = (λy.M[x/y])，其中M[x/y]意思是把自由出现的x替换成y。跟一阶逻辑量词的替换规则一模一样，例如：λx.(λx.x) x = λy.(λx.x) y；
  2. (β-归约) 定义了函数的作用：(λx.M) N = M[x/N]；
  3. (η-变换) 明确了函数何时相等，有点像集合论中的外延公理：λx.f x = f。
• 由于等词的存在，其实还有两个隐含的推理规则：
  1. (eq1) M = M是公理；
  2. (eq2) 如果有M = N成立，则可以在任意$\lambda$项中将它们互相替换。

提下关于括号的简写。如果没有括号，则“λx.”后面的管辖范围尽可能长，比如λx.M N代表(λx.(M N))而不是((λx.M) N)。

为什么要用“λ”表示函数呢？“f(x)”不挺好吗？那是因为当我们写下“f(x)”时，已经默认给函数起了名字“f”了。“λ”给了一种表达匿名函数的方法，现在很多程序语言都在使用，不过为了输入方便，一般不用符号“λ”而是“function”这类固定的单词了。注意λ演算中的函数都只有一个参数，然而由于多元函数能够看作返回函数的函数，因此这并不是个问题。

基本的$\lambda$演算可用于建构布尔值，算术，数据结构和递归的模型。这些东西本质上全都是函数，比如定义TRUE为λx.λy.x，可理解为一个永远返回第一个参数的二元函数f(x,y)=x；定义FALSE为λx.λy.y，可理解为一个永远返回第二个参数的二元函数f(x,y)=y。读者可以自行使用形式系统的规则验证下面定义的函数确实能实现相应的布尔逻辑运算：
AND := λp.λq.p q FALSE
OR := λp.λq.p TRUE q
NOT := λp.p FALSE TRUE
更多无类型$\lambda$演算内容见维基百科。

带类型的Lambda演算

无类型$\lambda$演算有时会产生一些问题，比如β-归约看似是化简函数，但有时却会让函数变得更复杂，比如尝试使用β-归约化简表达式“(λx:x x)(λx:x x)”会发现化简前后完全一样，而表达式“(λx:(x x) x)(λx:(x x) x)”会“化简”为“((λx:x x x) (λx:x x x)) (λx:x x x)”，继续β-归约得到“(((λx:x x x) (λx:x x x)) (λx:x x x)) (λx:x x x)”……反而变得越来越长且永远停不下来。这也导致致不存在一个通用的算法判定两个lambda项是否相等。类型论使用的就是带类型的Lambda演算，它通过引入类型，限制了上面那种无休止的循环自身作用，其规则大致如下：

• 除了等词符号“=”可断言两项相等构成命题，还引入了类型断言符号“:”断言值的类型，它也构成命题
• 定义λ函数时必须说明参数的类型，类型本身也是项。比如(λx:A.M)不能只写成(λx.M)
• 引入两个类型推导规则：
  1. (函数构造) 若假设x : A成立能在系统中推出y : B成立，则“(λx:A.y) : A → B”成立；
  2. (函数应用) 若f : A → B且x : A成立，则“f x : B”成立。这个规则的意思是，如果函数f的类型是A → B，且x的类型是A，则函数作用的结果f(x)的类型就是B；

注：如果函数参数与作用对象类型不同，则没有推理规则能够推出该表达式的类型，即发生了类似编译器检查到类型不匹配的错误。

下面我们重新来写一遍A → B与B → C推出A → C的证明：

• 1）f : A → B (已知条件)
• 2）g : B → C (已知条件)
• 3）引入假设 x : A
  • 4）f x : B (函数应用1,3)
  • 5）g (f x) : C (函数应用2,4)
• 6）(λx:A.g (f x)) : A → C (函数构造3,5)

注意由于推理规则中有假设的存在，所以每一步推导都要指明当前的假设上下文：缩进的4、5拥有假设3，而其余的假设上下文为空。类型论在函数内部把函数的参数与假设的概念统一了，相当于演绎元定理的作用，因此我们也可以证明下面这个类型是居留的，即存在某个值是该类型：
? : (A → B) → ((B → C) → (A → C))
推导过程其实都是把上面本来已知的f、g变成假设而已：

• 1）引入假设 f : A → B
  • 2）引入假设 g : B → C
    • 3）引入假设 x : A
      • 4）f x : B (函数应用1,3)
      • 5）g (f x) : C (函数应用2,4)
    • 6）(λx:A.g (f x)) : A → C (函数构造3,5)
  • 7）(λg:B → C.λx:A.g (f x)) : (B → C) → (A → C) (函数构造2,6)
• 8）(λf:A → B.λg:B → C.λx:A.g (f x)) : (A → B) → ((B → C) → (A → C)) (函数构造1,7)

是不是看起来有些复杂？如果我们熟悉了类型论的形式系统，可以这样从要证明的目标倒着往回写：

1. • 假设上下文：空
   • 待构造的证据：? : (A → B) → ((B → C) → (A → C))
   • 证明目标：? : (A → B) → ((B → C) → (A → C))

引入假设 f : A → B

2. • 假设上下文：f : A → B
   • 待构造的证据：λf:A → B.? : (A → B) → ((B → C) → (A → C))
   • 证明目标：? : ((B → C) → (A → C))

引入假设 g : B → C

3. • 假设上下文：f : A → B、g : B → C
   • 待构造的证据：λf:A → B.λg:B → C.? : (A → B) → ((B → C) → (A → C))
   • 证明目标：? : (A → C)

引入假设 x : A

4. • 假设上下文：f : A → B、g : B → C、x : A
   • 待构造的证据：λf:A → B.λg:B → C.λx:A.? : (A → B) → ((B → C) → (A → C))
   • 证明目标：? : C

? 处填入值 g (f x)，满足证明目标。

5. 证毕，得到完整的证据(λf:A → B.λg:B → C.λx:A.g (f x)) : (A → B) → ((B → C) → (A → C))

每次引入假设时其实就在构建函数，只不过还不知道函数体内“?”处该填入什么值，于是我们将证明目标转移到构造这个值上来，直到最后所有留空的值都填完，整个值就构造完毕，命题也就有了证明。以上这种格式步骤其实是目前计算机证明辅助工具（如Coq、LEAN等）几乎都在用的书写证明的方法。一般将引入假设写作“intro”，填入值写作“apply”或“exact”。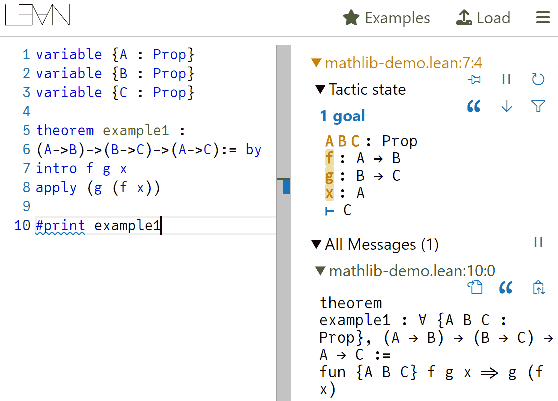
或许你觉得不如直接一口气写出表达式来得痛快，并不习惯用证明助手，后面将看到随着要证明的命题越来越复杂，这种能帮我们倒推目标的证明助手是刚需的，因为实际使用证明助手时其实只需要不断完成证明目标就行，目前构造出的证据长什么样这些细节都由计算机自动把关检查，可以少操不少心。比如上面证明命题(A → B) → ((B → C) → (A → C))，你只需要告诉证明助手以下三件事即可：

1. 依次引入假设f、g、x； (LEAN中写作intro f g x)
2. 填入值g (f x)。 (LEAN中写作apply f (g x))
   剩下的都是计算机自动去完成类型检查与生成证据。

依赖值类型、相等类型与定义相等

个人认为理解带类型的Lambda演算并不困难。下一个东西很可能是开始不太好理解的一个拦路虎：依赖值类型。它是由这个需求产生的：既然所有命题都是类型，那么“1=1”、“2=2”当然也该是类型。注意不要跟Lambda演算里面的相等混淆：涉及相等的命题仅仅只是一个类型而已，那种通过(α-变换)、(β-归约)定义的相等叫做“定义相等”的，它们在形式系统里永远视为无条件相等。为了区别两者，我把命题相等暂时写作(1 eq 1)和(2 eq 2)。在一阶逻辑里“1=1”、“2=2”是从等词公理里面直接得到的，因此类型论中也要引入一个“相等公理”的规则，即直接给出一个类型为a eq a的值：

• 对任意的项$a$，都存在项“$\mathrm{refl}_a $”，且有类型断言“$\mathrm{refl}_a : a\ \mathrm {eq}\ a$”成立。

注意类型论不再是简单的Lambda演算，因为Lambda演算中的“原子项”只能是变量或Lambda表达式，而类型论中还允许常量符号的存在，比如refl就是个常量符号。这个refl是反射（relexivity）的缩写，代表等式的自反性。设$\mathrm A$是某给定的类型，我们要证明对任意的$x:\mathrm A$，都有$x\ \mathrm {eq}\ x$”成立，这就意味着，我们需要构造一个函数，它随便接收一个变量$x:\mathrm A$，就能输出一个类型为“$x\ \mathrm {eq}\ x$”的变量。这个函数很好构造：它就是：$\lambda x : \mathrm A. \mathrm{refl}_x$。然而这个函数的类型是什么呢？可以想象，假设$A$代表自然数类型，如果输入1，则输出$\mathrm{refl}_1$，它的类型是1 eq 1；输入2则输出$\mathrm{refl}_2$，它的类型是2 eq 2，确实函数的输出类型依赖与输入。我们直接写成“$\mathrm A → x \ \mathrm {eq}\ x$”会让人困惑：箭头右边的x凭空就冒出来了，因此我们要先声明参数x，并引入符号$\prod$专门表示依赖函数：$\prod_{x:A} (x\ \mathrm {eq}\ x)$，在LEAN中则是这样表示依赖函数类型：“$(x:\mathrm A) → (x \ \mathrm {eq}\ x)$”。

非依赖的普通函数(→)其实是依赖函数($\Pi$)的特殊情况，我们约定，箭头符号其实就只是依赖函数$\Pi$的简写，即引入一个定义相等的断言：

$\prod_{x:A}$ B = A → B，若x不在B中自由出现。

比如函数类型(A → B) → ((B → C) → (A → C))也可以写作$\prod_{f:A → B} \prod_{g:B → C} \prod_{x:A} C$，更进一步，改写f与g的函数类型最终变成这样：$\prod_{f:\Pi_{x:A} B} \prod_{g:\Pi_{x:B} C} \prod_{x:A} C$。

为什么要用连乘符号表示依赖函数的确是个很让初学者困惑的地方，这里面虽然有一定的道理，但更多是历史遗留问题没必要去深究。我最先遇到这个类型时一直卡在去想那个连乘是什么含义，其实把连乘符号换成“$\forall$”还更方便理解（LEAN里面就是这么写的）。

选读：
我们看到命题相等类型与系统内的定义相等是两个概念，它们最大的区别是命题相等可以作为假设出现在函数参数中，而两个表达式是否定义相等则是固定的，无法在系统中表示“假设x与y定义相等”的概念。其实我们也可以强行加入一条规则让两种相等不再有本质区别：

• 若存在某个项x使得类型断言“x : a eq b”成立，则定义相等断言“a = b”成立。

然而事实上是没必要，且不应该的。因为判定一个项的类型往往是靠计算机系统自动完成的，如果把命题相等与定义相等等同，这就要求计算机在类型检查时有猜出“a = b”的证明步骤的能力。类型论中最复杂精妙的地方就是对相等的处理上，我们后面再来细说。

宇宙类型

有了依赖函数类型，我们不但能表达一阶逻辑，甚至还能表达二阶逻辑。比如“对任意命题A，都有A → A成立”这句话的量词作用在任意命题上，而一阶逻辑中量词只允许作用在项（代表集合、自然数等）的概念上，因此是妥妥的二阶逻辑中的命题。如果翻译成类型论，我们需要定义一个接受类型的函数，就会遇到类型的类型。类型论规定所有的类型的类型叫做全类，或宇宙（Universe），记作“U”（LEAN中记作“Type”）。但为了避免悖论，U自己的类型必须是更大的宇宙，记作U₁、然后U₁ : U₂ : U₃ : ……这样构成了无穷的类型宇宙层级，这些角标甚至可以拓展到序数，然而一般我们只用得到前一两个层级。
除了引入类型的类型规则，我们还将更新一下规则来确保系统的一致性：

• 只有A的类型是某个宇宙才能引入假设x : A。
• 若A:U_m，B:U_n，则$\prod_{x:A}$ B : U_max(m,n)，即函数类型所在的宇宙一定不比输入、输出的类型宇宙层级低。
• 若A:U_m，B:U_n，则A → B : U_max(m,n)（箭头类型是$\Pi$类型的特殊情况）

对任意命题A，都有A → A成立可以翻译成这个依赖函数类型是居留的：$$\prod_{A:\mathrm U} A → A$$下面直接给出构造的函数，读者可自行根据形式系统的规则对其类型进行验证：$$\lambda A:\mathrm U. \lambda x: A.x$$

简单归纳类型

类型论几乎没有公理，只有规则。刚才我们看到了普通函数与依赖函数类型、全类（宇宙）类型。其实类型论最基础的东西已经说完了，其它的类型（包括上面提到的命题相等类型eq）都是我们将要提到的归纳类型的特例。

归纳类型很简单，定义归纳类型，就是单纯将其可能的值全部列出来。比如只包含一个值的类型，记为True（游戏deductrium中的记法）或$\mathbb{1}$（同伦类型论（HoTT）书中的记法），向系统加入以下规则后就能愉快地使用该类型了：

• True : U
• * : True
  这里的星号代表True类型唯一的元素值，称之为类型True的构造子（constructor），来自同伦类型论书中的记法，游戏deductrium中用小写的“true”表示True的构造子。

我们也可以定义只包含两个值（构造子）的类型，记为Bool或$\mathbb{2}$，需要向系统加入以下规则：

• Bool : U
• 0b : Bool
• 1b : Bool

甚至可以构造不包含任何值的空类型，记为False或$\mathbb{0}$，由于没有值，因此目前仅需加入一条规则：

• False : U

看得出来True类型与Bool类型都代表恒为真的命题，而False类型则是恒为假的命题。读者可以自行验证下面的命题的证据：

• λx:True.x : True → True
• λx:False.x : False → False
• λx:False.* : False → True

然而我们无法证明True → False，这跟命题逻辑是保持一致的，事实上我们能够证明True → False为假命题，因为假设True → False成立我们就能推出False成立：

• λx:True → False. x * : (True → False) → False

在类型论中，我们将命题A的否定直接定义成“A → False”，而不是像命题逻辑把否定看作基本的逻辑符号。

归纳法则

虽然刚才我们定义出来的类型感觉很好用，但遇到稍微复杂的情况却难以应对，比如我们没有证据表明True类型中只有“*”这个唯一元素的事实，于是暂时无法构造出下面这个真命题的证据：

对任意的x:True，都有x 等于 *

解决方法很简单：把该事实作为公理加入进系统即可。但关于任意x:True的命题太多了，我们不可能全都作为形式系统的规则加入进去，于是可以制定这样的规则：要想定义一个对任意x:True都能输出指定类型C的函数，我们只需定义当x等于*时函数的值即可。将这句话翻译成公理“rec_True”，它是有两个参数的依赖函数，即：rec_True(C,val) : True → C，且rec_True(C,y) (*) = val。这可能是除依赖值函数外的第二个类型论学习之路上的“拦路虎”，它的困难之处在于符号复杂，经常容易被绕晕，但其中的原理却并不复杂，如果你看不太懂可以往后跳过。

我们向系统加入两条规则来描述它：

• rec_True : $\prod_{\mathrm C:\mathrm U}$ C → (True → C)
• 对任意的项C、y，都有定义相等断言“rec_True C y * = y”成立

第二个规则表示我们用rec_True C y定义出来的函数在x为*时值就是y，因此直接是定义相等。可惜这样定义出来的只是普通函数，并不依赖值，还是无法构造“x eq *”这样的命题证据。下面我们把C换成依赖x的类型，即一个输入一个x:True就输出一个类型的函数“C: True → U”（把这里理解了就成功一半了）。

引入rec_True函数的依赖函数版本ind_True，同样向系统加入两条规则来描述它：

• ind_True : $\prod_{\mathrm C:\mathrm{True} → \mathrm U}$ ((C *) → $\prod_{x:\mathrm{True}}$C x)
• 对任意的项C、y，都有断言“ind_True C y * = y”成立

如果把C(x):U看作关于x的命题，则“ind_True”在说：随便给定关于x:True的命题C(x)，如果命题C(*)成立，则对任何x:True，C(x)都成立。

读者可以验证下面的类型断言确实证明了我们的命题：

ind_True (λx:True → x eq *) refl_* : $\prod_{x:\mathrm{True}}$x eq *

如果你觉得这些依赖函数表达式看上去很晕，大概知道它们就是表达“True类型只有唯一值*”的公理即可，或者也可以试着玩玩Deductrium中的类型论形式系统，把鼠标悬停在每一项上都会显示它的类型，应该对理解有很大帮助。Deductrium中要在比较后期才能解锁类型论，没有精力的读者可以去Deductrium的创造模式直接体验：点击类型层，在定理列表中输入表达式，系统就会自动计算它的类型，也可以输入A : B、A === B这种类型断言和定义相等断言表达式，系统会自动判断输入的断言是否正确，你也可以使用xxx := XXX的形式将XXX简写为xxx，定义后即可在位于其后面的定理中（按加号按钮添加）使用。

下面回归正题。每一种类型都有相应的归纳法则，比如“ind_Bool”、“ind_False”、甚至“ind_eq”等等。
我们大概说说它们代表的含义，不再写出其类型与运算法则。

• ind_Bool：对任意依赖类型C(x)，只要给出了C(0b)与C(1b)的值，就能构造出依赖函数$\prod_{x:\mathrm{Bool}}$C(x)；
• ind_False：对任意依赖类型C(x)，什么值都不用给，就能构造出依赖函数$\prod_{x:\mathrm{False}}$C(x)；
• ind_eq：给定类型A，对任意依赖类型C(x:A,y:A,m: x eq y)，只要给出了C(x,x,refl_x)，就能构造出依赖函数$\prod_{x,y:\mathrm{A}}\prod_{m:\mathrm{x eq y}}$C(x,y,m)；

说明1. 这里的ind_False其实暗含了“否定爆炸”原理：对于任何命题，我们都能构造出一个接收False类型变量的函数来输出它，因此只要有了False类型的值，我们就能证明一切。
说明2. eq类型其实不是一个简单的类型，它是带有A、x、y三个参数的复杂类型，然而它只有一种构造方法，那就是refl_a : a eq a，因此要想构造关于eq类型的函数，就只需考虑x=y(即定义相等)这种情况即可。

同样我们可以归纳定义这些带参数的复杂类型：

• 有序数对，也叫积类型： (a,b) : A x B，它由一个带两个参数（a:A与b:B）的的构造子构成。要构造类型A x B必须同时给出A与B的元素，因此 A x B 可翻译为命题“A且B”。
• 依赖积类型，若a:A且b:B(a)，则(a,b) : $\sum_{x:A}$ B(x)，它的构造子类型从简单函数变成了依赖函数。由于只要给出任意一组a:A且b:B(a)就能构造依赖积类型，因此$\sum_{x:A}$ B(x)可翻译为“存在x:A使得B(x)成立”。
• 和类型A + B，它类似布尔类型，有两个构造子：要么由第一个带参数a:A的构造子构造，要么由另一个带参数的b:B构造子构造。要构造类型A + B要么给出A的元素要么给出B的元素，因此 A + B 可翻译为命题“A或B”。

由于它们都是归纳类型，因此无一例外都有相应的“ind_xxxx”函数，它们都在断言，给定一个带参数的命题C(x)，只要把这些归纳类型的所有构造子的所有情况都分类讨论了，则可以证明对任意的x，命题C(x)都成立。这里就不展开介绍具体细节了。

自然数与数学归纳法

我们最后再来看自然数类型nat : U，它有两个构造子“0”和“succ”：

• 0 : nat
• succ : nat → nat

这个succ是什么意思呢？它说明如果n是自然数，则succ n也是。也就是说归纳类型中的参数是可以递归的，甚至两个归纳类型的构造子还可以“交叉”构造等等。因此构造子的数量并不等于该类型中真正元素的数量。ind_nat函数正好就等价于数学归纳法：要证明一个命题C(n)对所有自然数n都成立，则需要证明它对0（即C(0)）和succ也成立。succ是带参数的，因此要证对所有的x: nat，都有命题对succ x成立（$\prod_{x:nat}$ C(succ x)）。然而自然数的递归性还没体现出来：所有元素都只能由0或succ生成出来，因此succ x中的x肯定早就是满足命题的自然数，即其实还有个递归给我们的已知条件C(x)，加上后就变成$\prod_{x:nat}$C(x) → C(succ x)。现在它已经跟数学归纳法一模一样了：首先要证明C(0)成立，然后是证明对任意自然数x，都有“从对x成立推出对x+1 (即succ x)成立”。

以上是用命题的思考角度来理解ind_nat函数。现在以函数求值的方式重新审视一遍它：要定义一个关于自然数的函数f，首先要定义其在0处的值f(0)，然后，对于任意x，其在succ x处的值f(succ x)不仅可以依赖于x，还可以依赖于之前的f(x)的值，这就允许我们定义递归函数。其实加法、乘法、指数等原始递归运算全都可以用ind_nat函数写出来。有兴趣可以参考维基百科。

类型论与经典逻辑的区别

下面我们来总结对比一下类型论与集合论：

项目	类型论	集合论
假设推演	普通函数	逻辑蕴含符号
否定	命题推出False	否定符号
任意	依赖函数	一阶逻辑量词“任意”
存在	依赖积类型	量词“任意”与否定的组合
与	积类型	否定与逻辑蕴含组合实现
或	和类型	否定与逻辑蕴含组合实现

我们发现一阶逻辑中对待任意与存在、对待与和或是差不多的，而类型论中却差异很大。一阶逻辑属于“经典逻辑”，即承认同一律（$a=a$）、排中律($A\lor\lnot A$)、无矛盾律($\lnot(A\land\lnot A)$)。然而类型论并不承认排中律。排中律在说：一个命题要么是真的要么就是假的。这显然是正确的。类型论是为了计算数学而设计的，它的每个“证据”都是可计算的。哥德尔不完备性定理说不是所有命题都是可证明的，也就是说存在命题不能证明也不能证伪。类型论构造“或”的证据时，必须指明选择哪一边的构造子来构造，这是有额外信息的，对于哥德尔命题显然选哪边都构造不出来。其实减少否定符号的很多命题都与排中律等价，它们都不能在类型论中证明，比如双重否定消去律：

• (¬¬A → A)

相反，类型论证明双重否定介入则没问题：
(λA:U. λx:A. λy:A → False. y x) : (A → ((A → False) → False)) = (A → ¬¬A)

注意不代表必须要出现否定符号才可能蕴含排中律，这个看似人畜无害的“皮尔士定律”也蕴含排中律，从而不可证：((P → Q) → P) → P。

我们完全可以向类型论中引入公理来解决这个问题，但这样可计算性遇到公理后就进行不下去了。其实很多时候并不需要排中律也能证明绝大多数命题了。后面我们将看到同伦类型论将把排中律证伪。

常见否定问题的判定

不知大家有没有想过类型论中如何证明0不等于1呢？我们只能用间接的方法来证明：先通过“ind_nat”定义一个函数f : nat → U，把0映射到True，把1映射到False，再利用0与1相等的假设，通过ind_eq得到若f(0)成立则f(1)就成立，因而得到命题False成立。其实所有的构造子都可以用类似的方法附上不同的真假值来推出矛盾，这叫做归纳类型构造子的普遍性质——“不交性”。

同伦类型论简介

粗略来说同伦类型论就是专门研究相等类型的理论。它指出类型可按相等类型的性质大至分为以下几类：

1. 像纯命题的类型A：类似True类型，A中只有一个元素，对于任意的a, b : A，都有a eq b成立。
2. 像集合的类型A：对于任意的a : A，类型a eq a的元素都是唯一的。
3. 其它高阶同伦类型：对于对于任意的a : A，类型a eq a的元素不只有refl_a，还可能存在与其不相等的东西。

下面是解释：

1. 对于命题来说，无论证据是什么，都仅代表它成立了，不需要其它额外的信息，因此，一个“纯粹”的命题的类型应该满足内部所有元素都相等。
2. 对于集合来说，不再要求只能有唯一的元素，但每个元素都相当于一个个孤立的点，没有其它额外的结构。
3. 高阶同伦类型可以看作是一种拓扑空间：每个值就是空间中的点，定义相等的值视为同一点，命题相等但不定义相等的两点视为有一条路径将它们连接在了一起，命题相等的证据就是这一条条的路径。路径之间也可以判断是否相等，相等的路径在拓扑空间中是同伦的——即存在更高维的路径链接它们——存在一个二维面能让一条路径在其上面连续变形到另一条路径。如果存在不同于refl_a的路径，说明从点a出发的一个圈不能够连续收缩到一点。

为什么能把相等类型看成路径？很容易通过“ind_eq”函数构造等式的自反性、传递性的证明，即构造出函数：

• (x eq y) → (y eq x)
• (x eq y) → ((y eq z) → (x eq z))

这些函数对应着同伦路径的逆与连接操作。如果读者不太清楚什么是同伦，可以参考《代数拓扑简介（上）：同伦论》。

“同构即相等”公理

可除了等式自反性的唯一证据refl之外，这些其它东西到底是什么呢？同伦类型论加入了 “同构即相等”公理——Univalence Axiom，简称ua，有人翻译为“一价公理”或“单价公理”。首先定义两个类型之间如果能定义出双射函数，则称这两个类型等价，记作“A ≃ B”，具体定义表达式是一些依赖的有序对（前面介绍过的依赖积类型），里面装了双射函数与其确实是双射的证据等等，写出来有些复杂，请参考《HoTT》（同伦类型论）这本书。ua公理断言以下命题成立：

(A ≃ B) ≃ (A eq B)

注意等价符号代表着双射，它有两个方向，一个方向是说存在某个值有类型：

• idtoeqv : (A eq B) → (A ≃ B)

这很显然，任意类型都可以定义出自己到自己的双射，这里规定选最简单的恒等映射，即输入一个$refl_A$（A eq A的证据），idtoeqv函数就能给出A到自身的恒等映射，即A ≃ A的证据。
另一个方向不加入公理就无法证明，于是需要向系统中加入以下公理：

1. ua : (A ≃ B) → (A eq B)
2. ua与idtoeqv互为逆映射

这代表类型A与B之间每种不同的双射都对应着类型A与类型B相等的不同证据。特别地，恒等映射对应refl。

同伦类型论除了引入“同构即相等”公理外，还引入了高阶相等类型构造子的归纳类型。下面我们给出圆周$S^1$这个归纳类型的构造子：

• base : $S^1$
• loop : base eq base

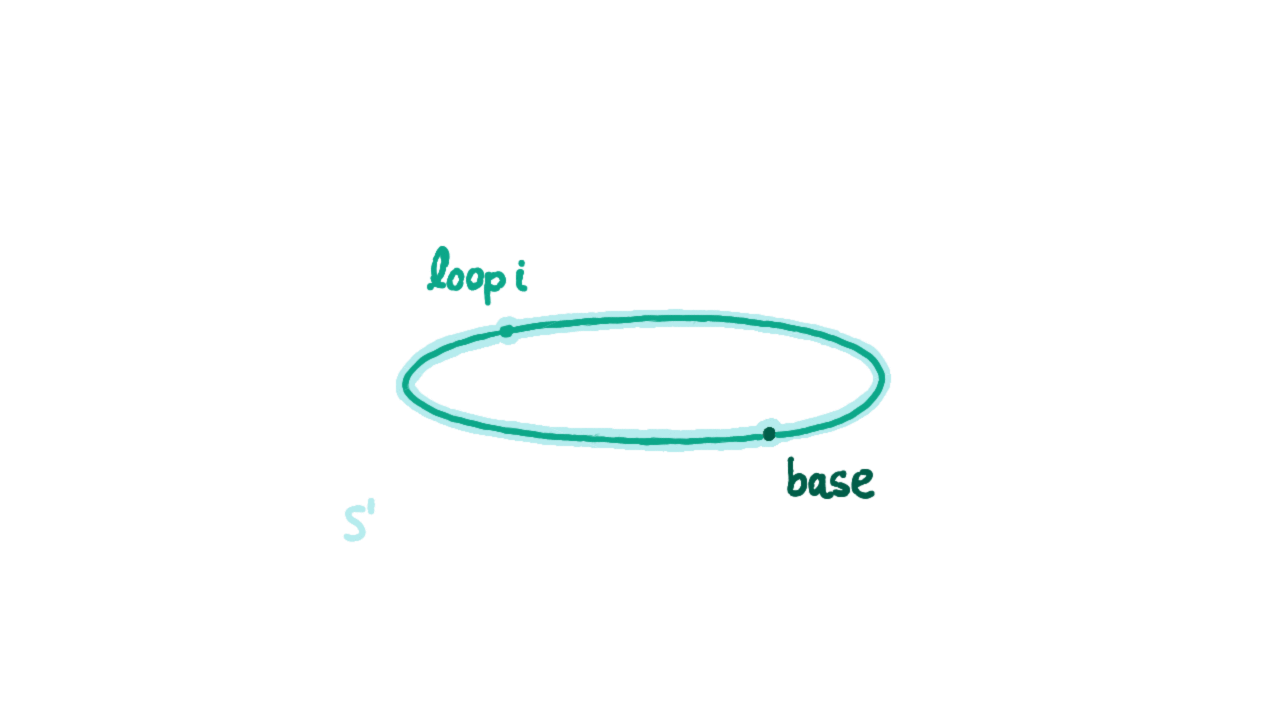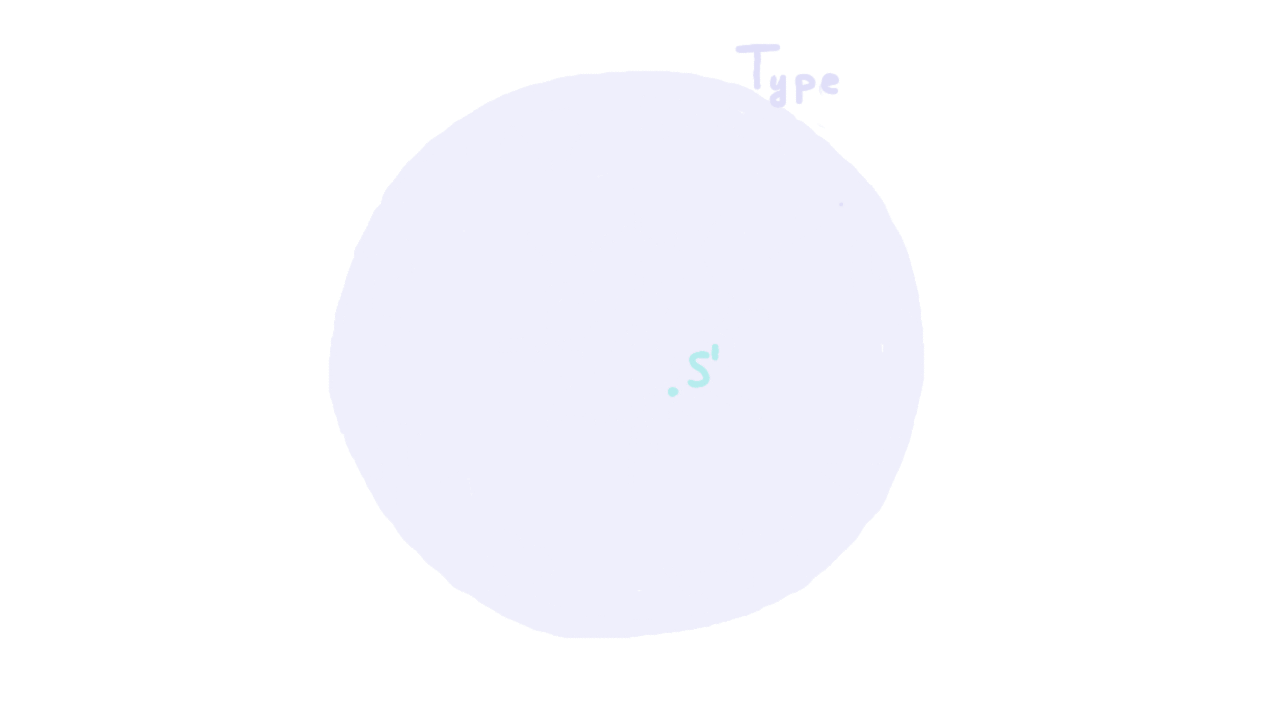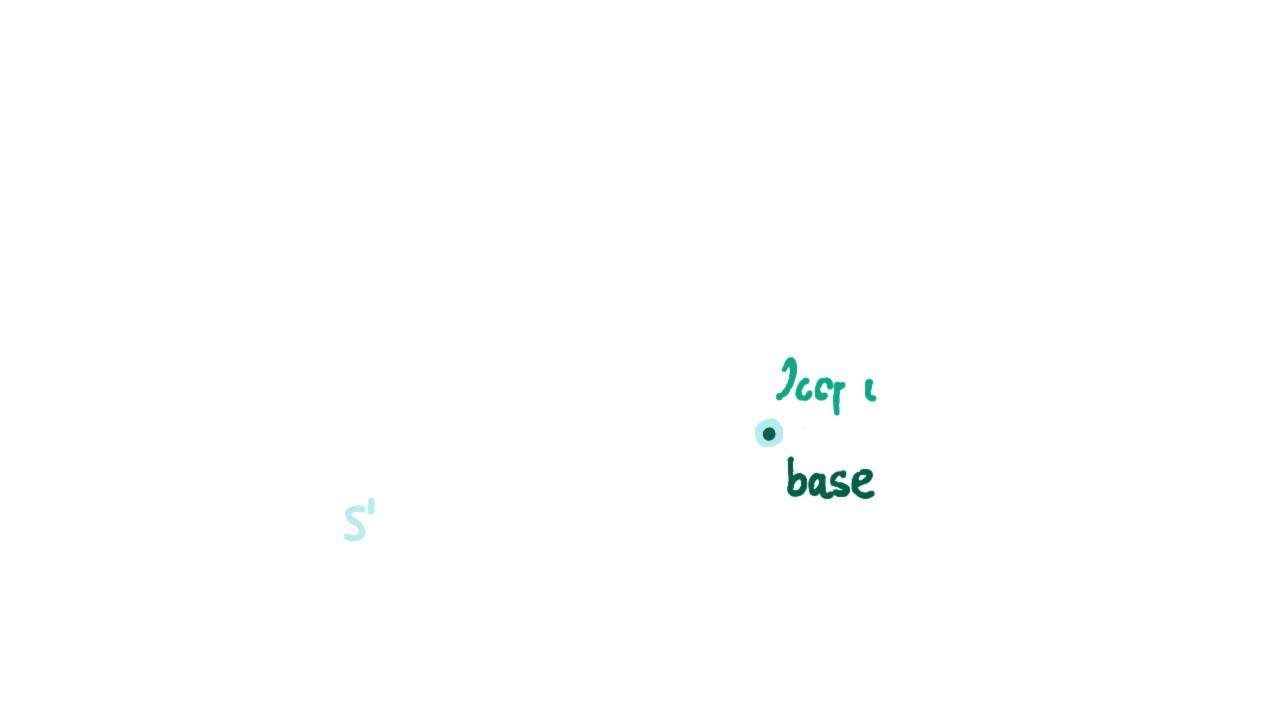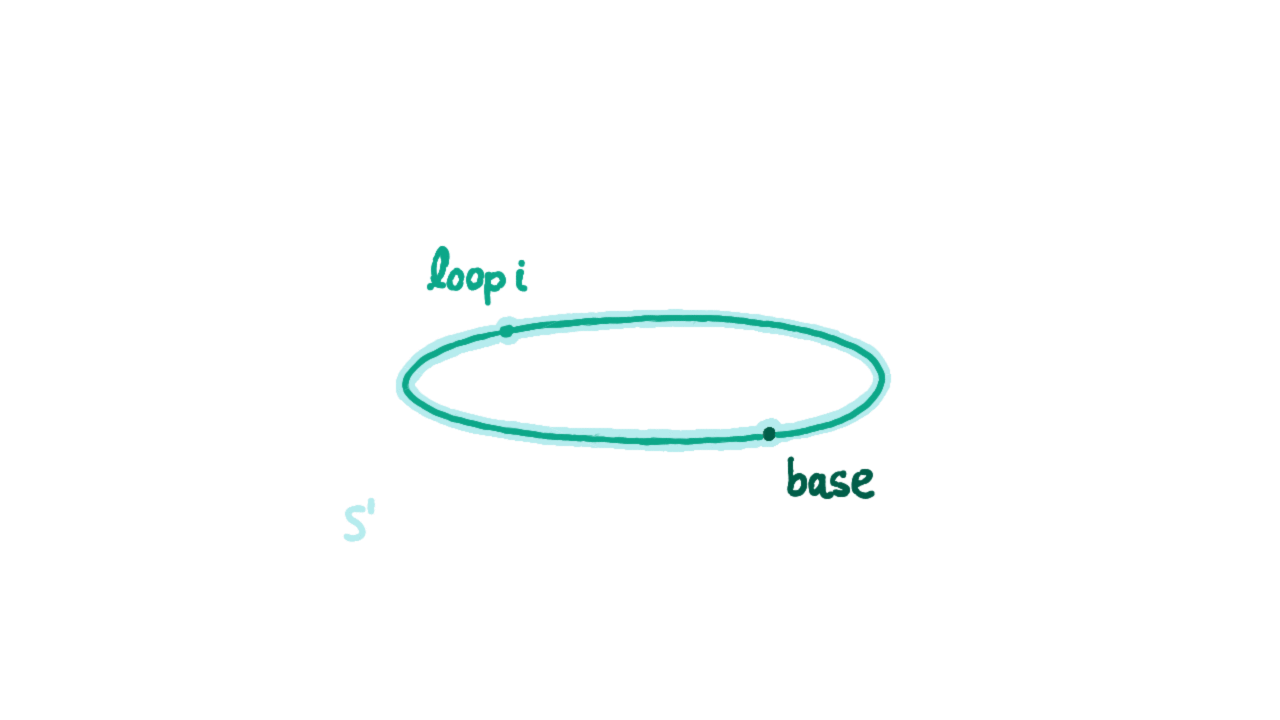
注意这里的loop是不同于refl的（后面马上证明）。我们把refl理解为圆周上缩成一点的路径，把loop理解为顺时针绕圆周一圈的路径，等式的自反性、传递性证据相当于路径取逆、路径连接，通过它们可以生成圆周上的整个基本群，即类型为base eq base的值的所有可能情况。注意，要在类型$S^1$上定义函数（即ind_S1），则除了指定该函数在base处的值，还必需要指定把那个loop映射到哪。

有了ind_$S^1$，我们就能够像证明0不等于1那样证明loop等于refl能够推出矛盾。我提供一个可能的思路：通过ind_$S^1$定义一个函数f : $S^1$ → U，它将base映射到布尔类型Bool : U，根据上一小节的同构即相等公理可知，相等类型Bool=Bool也有两个元素，一个是refl，另一个则是将0b(下图中的false)与1b(下图中的true)互换的自同构映射g生成的，记作ua(g) : Bool=Bool。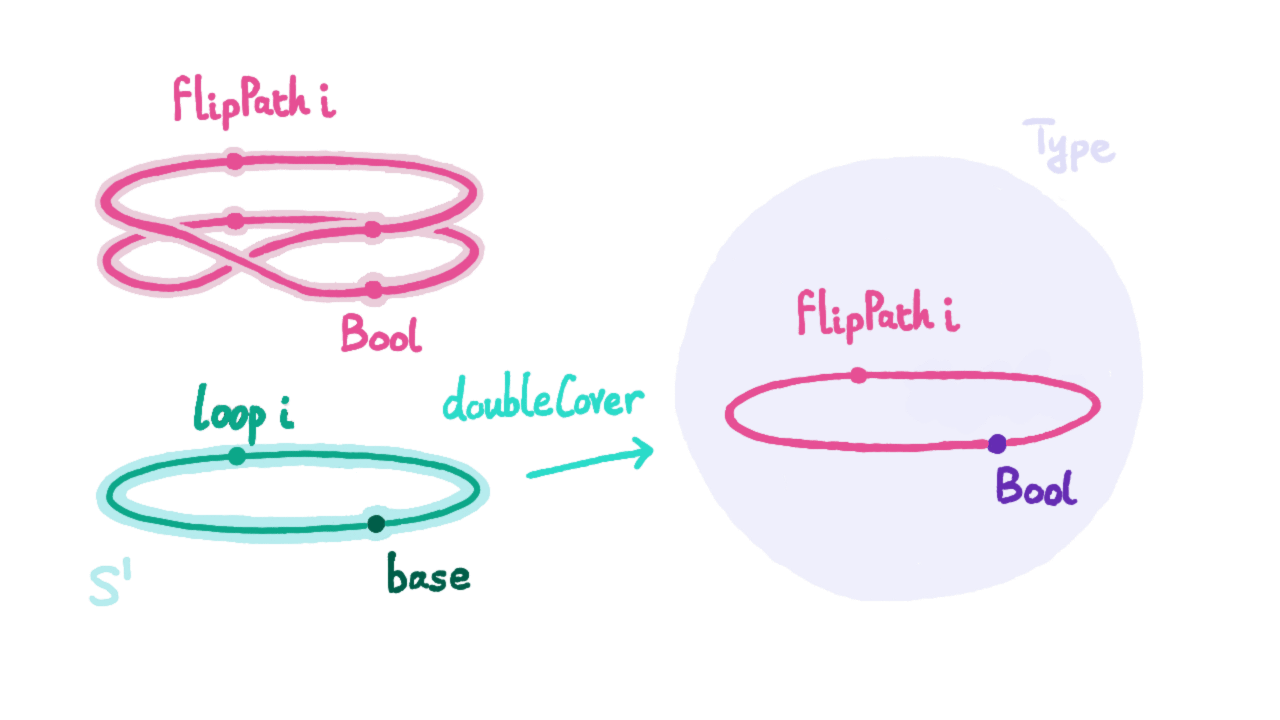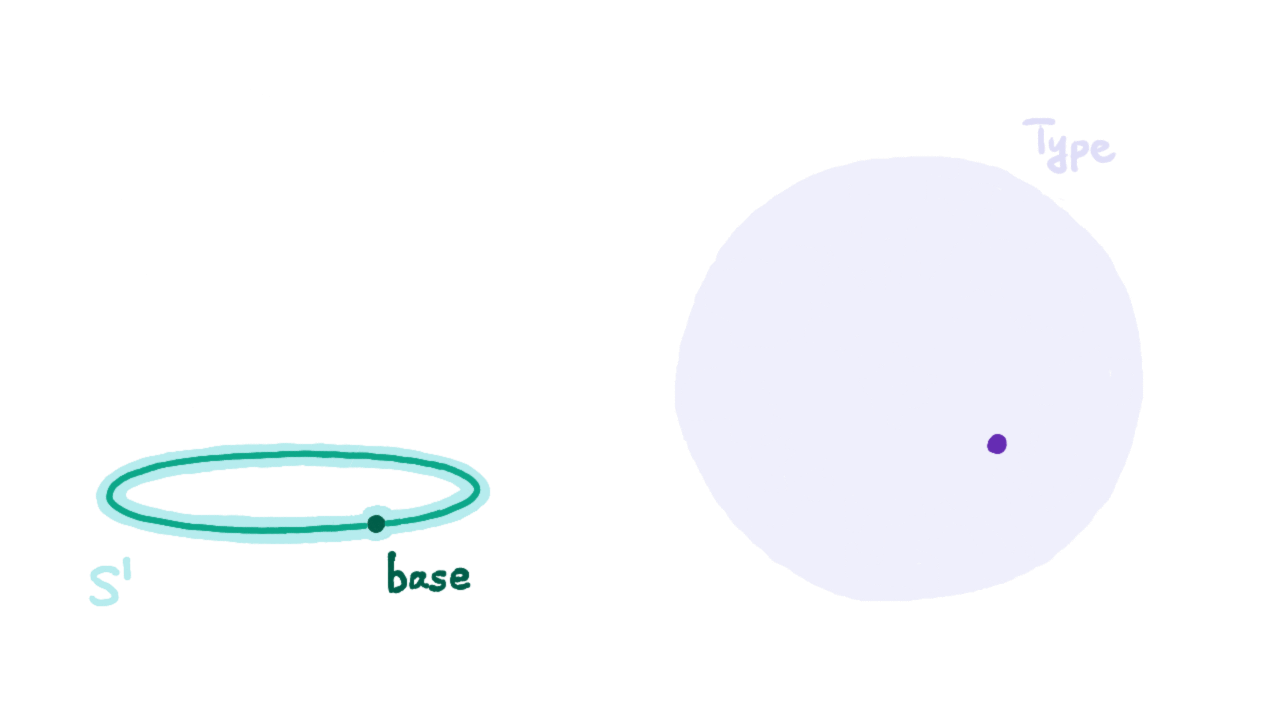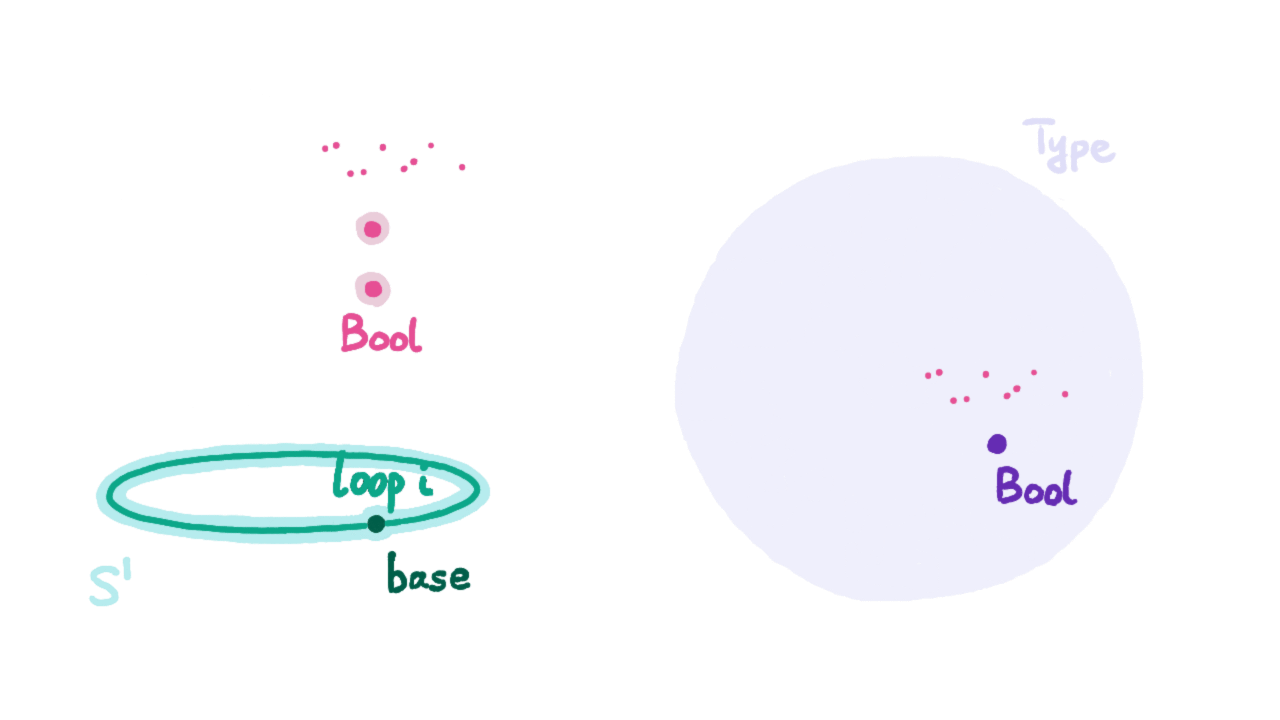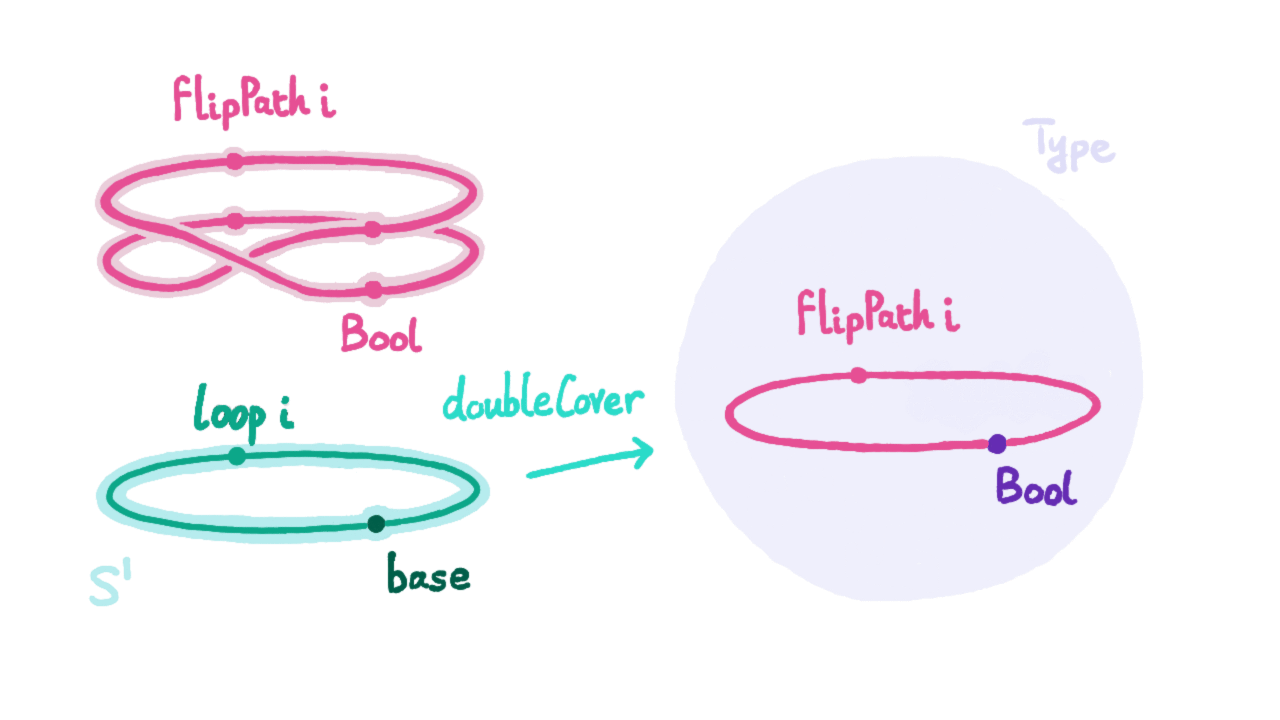
我们现在将loop映射到ua(g)，由于我们假设loop=refl，于是该函数将等价关系传递到了Bool之中，得到将0b与1b互换的自同构映射生成的p : Bool=Bool与refl : Bool=Bool相等。然而当我们试用这两个相等关系来映射Bool类型中的变量是结果却不同，按假设它们应该相同，即得到0b=1b。

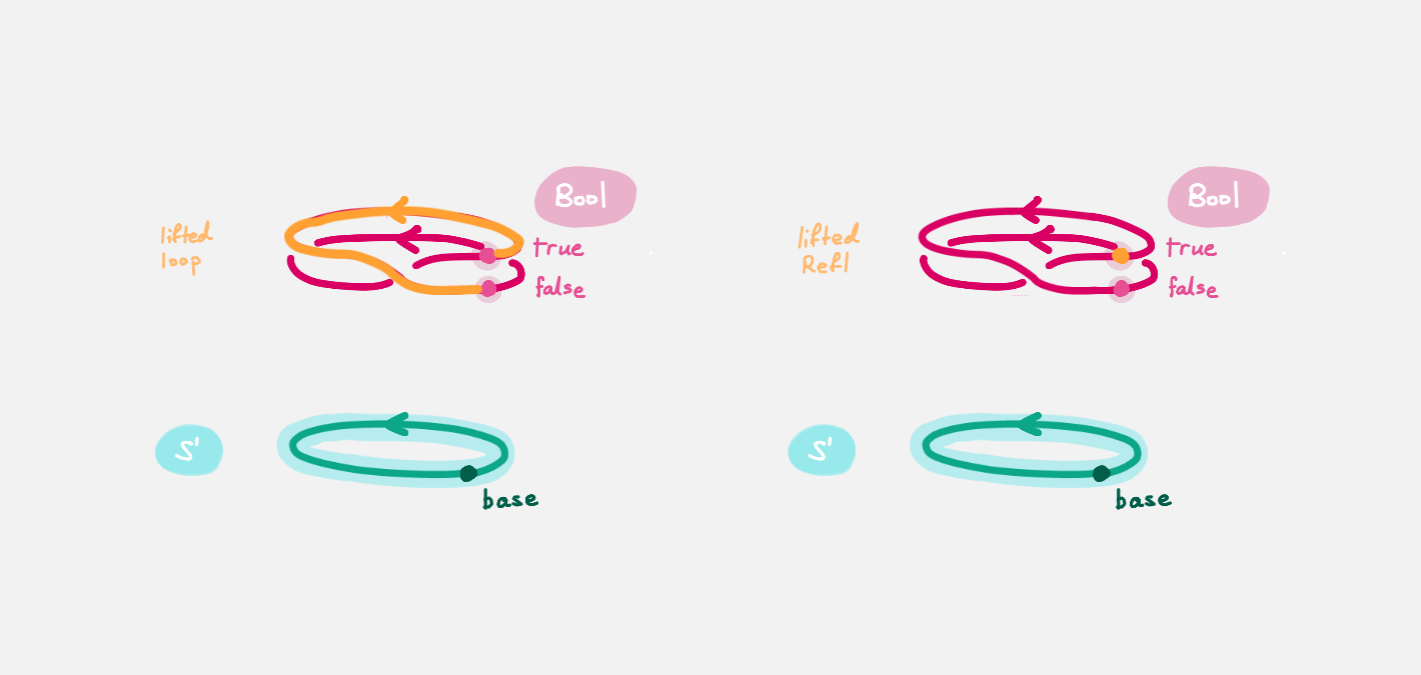
而球面$S^2$ : U这个归纳类型的构造子则是这样：

• base : $S^2$
• loop : refl_base eq refl_base

同伦类型论甚至可以发展出理论计算超球面$\mathbb S^n$的一部分同伦群，我确实也没精力看到那了，这里就没法介绍了。

同伦类型论与排中律

同伦类型论加入了这条公理“ua”后，导致排中律不再成立，即我们可以构造出下面类型的值：

“( $\prod_{A:\mathrm U}$ (A + (A → False)) ) → False”

之前我们说过排中律等价于双重否定消去律，因此我们只需要给出一个具体的f : $\prod_{A:\mathrm U}$ ((A → False) → False) → A，能得到False类型的值就能完成原命题的证明（转换步骤留给读者思考）。

下面我们来具体构造：考察(Bool → False) → False的元素我们知道“Bool → False”是假命题，根据否定爆炸原理（由ind_False构造）可以得到任何命题都成立，因此在任给一个x:Bool → False的前提之下不仅能推出False，还能推出任意(Bool → False) → False中的两个元素u、v得到的u(x)与v(x)都相等。换句话说，函数u和v在任意的输入x下都由相同的输出，因此通过函数的外延公理（可由同伦类型论的公理得到）可证明u与v相等，即(Bool → False) → False的所有元素均彼此相等。

有了以上铺垫，下面就可以正式构造矛盾了。前面说过要构造一个具体的f : $\prod_{A:\mathrm U}$ ((A → False) → False) → A，能得到矛盾（False类型的值）就算完成任务。下面我们考察f(Bool)，它的类型是((Bool → False) → False) → Bool。对于布尔类型Bool，我们通过ind_Bool构造函数 e : Bool → Bool，使得：e(0b)=1b、e(1b)=0b。（又是它来构造反面证据！）很容易看出函数e是Bool类型到Bool类型之间的双射，即有(Bool ≃ Bool)成立。根据ua公理，ua(e)是一条(Bool eq Bool)的证据，且它跟恒等映射id得到的ua(id)=refl_Bool是不同的证据。

函数f不仅把A类型的值映射到了((A → False) → False) → A，它也把A类型上的相等路径映射到了后者的相等路径。我们看到，由于(Bool → False) → False类型只有一个值，无论是Bool中的refl还是ua(e)都将在此映射到该值的单位路径refl。对于任意的u:(Bool → False) → False，根据相等的映射传递关系（具体细节参考《HoTT》中的3.2小节）我们都有e(f(2)(u)) = f(2)(u)，而函数e是交换0b与1b的映射，不是恒等映射，推出了矛盾。

通过“截断”构造纯命题

我们看到，排中律不成立的根源在于Bool类型有了多余的元素，而类型(Bool → False) → False又只有单一的元素造成的。对于前面说过那些纯命题的类型是不会产生矛盾的，因此在同伦类型论中可引入“狭义”的排中律公理：

LEM : $\prod_{A:\mathrm U}$ isProp(A) → (A + (A → False))

isProp(A)代表“A是纯命题类型”，即任意两个A中的元素均相等，即为$\Pi$x:A,$\Pi$y:A, x eq y的缩写。注意“A是纯命题类型”这个条件是必须的，否则正如我们前面分析的会推出矛盾。

命题逻辑A或B对应的A+B这种类型有两个不同的构造子，因此不是纯命题。通过带参数的高阶归纳类型可以引入一种“截断”机制，强行定义一个新类型将其纯命题化：
对任意的A:U，都有：

• 对任意的a:A，都有|a| : ||A||；
• 对任意的x,y:||A||，都有x eq y。

这样加上“||”后就能把所有命题变成纯命题，然后才能愉快地使用排中律。
使用这些“截断”技巧我们不难定义出拓扑学中的商空间等概念（将空间中的某些点或路径等视为等价来构造新空间），很多拓扑学中的操作都可以翻译为同伦类型论中的语言，比如我们还没提到拓扑学中的纤维丛其实就对应依赖函数类型。最后，选择公理也有类型论的版本，但也需要在单独作为公理来引入……

参考

同伦类型论有点像大数理论，都是最近还处在发展中的新理论。更加成熟的则是机器证明领域，相关的话题实在太多了，本文实在没有能力完全覆盖，请有兴趣的读者请自行探索：

• 在线版的证明器LEAN
• LEAN教程
• 在线版的证明器jsCoq
• Coq教程
• The HoTT Game（同伦类型论游戏）
• Homotopy Type Theory: Univalent Foundations of Mathematics（《HoTT》电子书）

最后再安利一下我制作的游戏Deductrium中的创造模式。