四维世界（十一）：元素周期表

这次我们来看看四维世界中的微观理论之元素周期律。四维原子结构一直是一件麻烦事：力的三次方反比衰减规律导致原子定态波函数不存在，科学界都公认四维世界中不可能有原子，也不可能构成物质，本文完。除了直接接受这个残酷现实，其实还是可以假设有四维世界原子，但其量子力学具体机制肯定跟三维理论完全不同。为了尽量保持跟我们世界的相似性，如果暂且不管力的三次方反比衰减规律，假设波函数在超球面各方向上的分布还是满足波动规律，则还是可以保留原子的电子亚层结构、元素周期律与分子结构，不足的就是电离能、活泼性、光谱等涉及整体能量等需要涉及径向方向的计算问题就完全无法预知结果了。所以，本文（包括整个四维世界系列）的“科学性”大打折扣，仅供娱乐与提供（写小说等）思路，请勿较真。

回顾：三维元素周期律

三维元素的周期律是怎么来的呢？简单来说，在微观世界里，一切东西都是量子波。原子核外的电子就是在原子核周围振动的驻波。通过数学方程求解出这些振动模式，叫做电子轨道。又由于电子波函数的特点使得两颗电子不能同时处于完全相同的振动模式，因此每个电子轨道中最多只能容纳两个自旋相反的电子，即泡利不相容原理。

如果读者看了上一篇文章四维空间（十三）：超球谐函数介绍的球谐函数，我们就可以开始排元素了：电子的波函数是在三维空间中振动的，除了球谐函数代表球面上的振动，还需要加上径向上的振动，总的振动次数代表着能量，即电子所在的“层”。总振动如果为0，就只有球对称的一种波函数，对应$1s$轨道。这个轨道里可以装一个或两个电子，对应氢与氦元素。

到了锂元素，能量最小的轨道被填满了，多出来的电子只能挤进下一层——振动为1的轨道。如果振动是径向方向，则波函数还是球对称的，对应$2s$轨道，如果振动是在球面上，则径向上不能再有振动，球面上将有三种振动模式，对应三个2p轨道：$p_x$、$p_y$、$p_z$。$s$轨道跟$p$轨道的区别仅在于角动量的大小。按理说电子只管能量的优先级来填，但实际情况是，电子与电子之间互相影响导致这些不同角量子数的轨道的能量实际并不相同，具体的能量遵循一张叫做“能级交错”的图，相信大家在高中化学中已经见到过了它。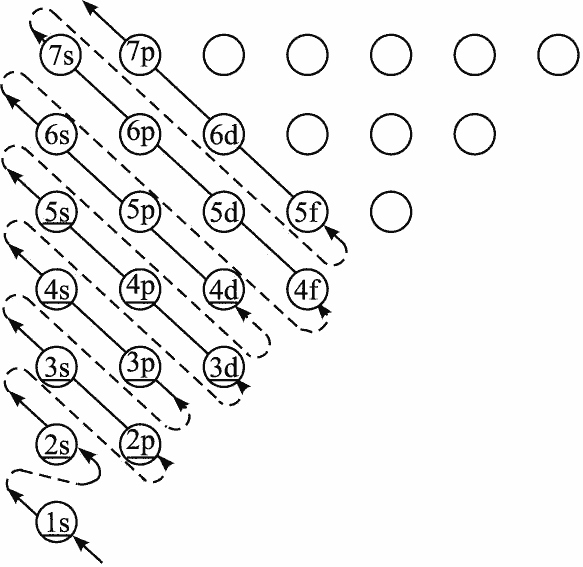

有了能级交错原理，继续按顺序填电子下去就可以解释为什么有主族、副族和锕系、镧系……总之，给定角量子数为$l$，就存在$2l+1$个简并轨道（意为这些轨道角量子数都一样），即每个电子层有最多有一个$s$轨道、3个$p$轨道、5个$d$轨道、7个$f$轨道……相信大家对三维周期表已经比较熟悉了（高中水平）。在继续看四维前，我们先来看看更简单的二维世界中的元素周期律来加深理解这其中的原理。

练习：二维元素周期律

《平面宇宙》这本书中早就设想过二维宇宙以及里面的元素周期表了。它假设电子还是有顺时针逆时针两个自旋态，也同样遵循能级交错图。我们在上一篇文章中也讨论过圆周上的振动，它们被简单地按振动次数分类，除了常数函数，每种振动次数下都有类似正弦与余弦两种相位的振动模式。振动次数正好对应角量子数，因此除了它的$s$轨道只有一个外，其它的轨道（$p$、$d$、$f$、$g$等）都是两个。每个轨道里最多填两个电子，按能级交错，就会得到下面这样的以每两行、每四列形状的锯齿形的周期表。下面的图片来自一个b站用户的专栏。

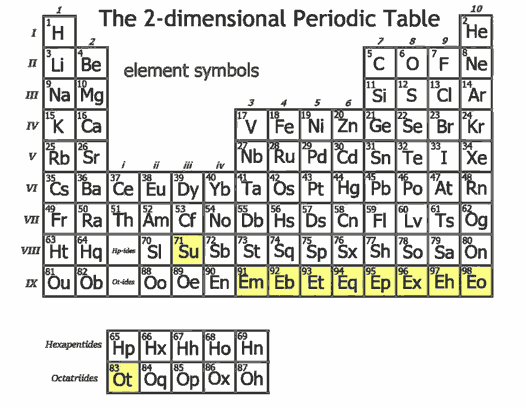
我们可从中看出，二维世界的主族、副族、镧系锕系的列数都只有4列了，明显比三维的短得多，导致作者根本没必要像三维世界的周期表那样把$f$轨道产生的镧系（Ce - Yb）锕系（Th - No）单独扔出来（到了$g$轨道作者才单独列出来）。从中可以看出，二维世界的元素丰富程度似乎要比三维少很多，除非超重元素比三维的稳定得多，只能往后面多排一些超重元素来凑够数量了。

二维世界中没有氮元素，碳过了直接就是氧。碳最外层只有3个电子，离6电子稳定结构还差3个，因此甲烷是CH₃而不再是CH₄。同理，乙烯的结构是直线型的H-C=C-H，不再有三键的乙炔存在。除了碳酸之外，不再存在其它的有机酸了，对于醛类也是，只有甲醛没有乙醛了。氧原子倒是没什么变化，水还是H₂O，氟元素及其它卤素不怎么受维度影响，跟三维的差不多。

尝试：四维元素周期律

终于轮到四维了。上一篇文章介绍的有亿点复杂的超球谐函数也总算可以开始为我们服务了。按照角量子数在超球各经纬线上的波动规律，我们可以得到不同亚层的简并轨道个数：$s$只有一个轨道，$p$有四个：$p_x$、$p_y$、$p_z$、$p_w$，$d$轨道与$f$轨道则是9个和16个，一般角量子数为$l$，则它有$l^2$个简并轨道。（注意无论选择Hopf坐标还是超球极坐标，虽然各轨道形状不太一样，但轨道的数量是一样的）掌握了这个规律后，就完全能够按照能级交错规律就能画出四维元素周期表了。Higher Space论坛上有人提出了四维元素周期表，他放了一个表格的截图，并为每种元素都命了名，取了元素符号：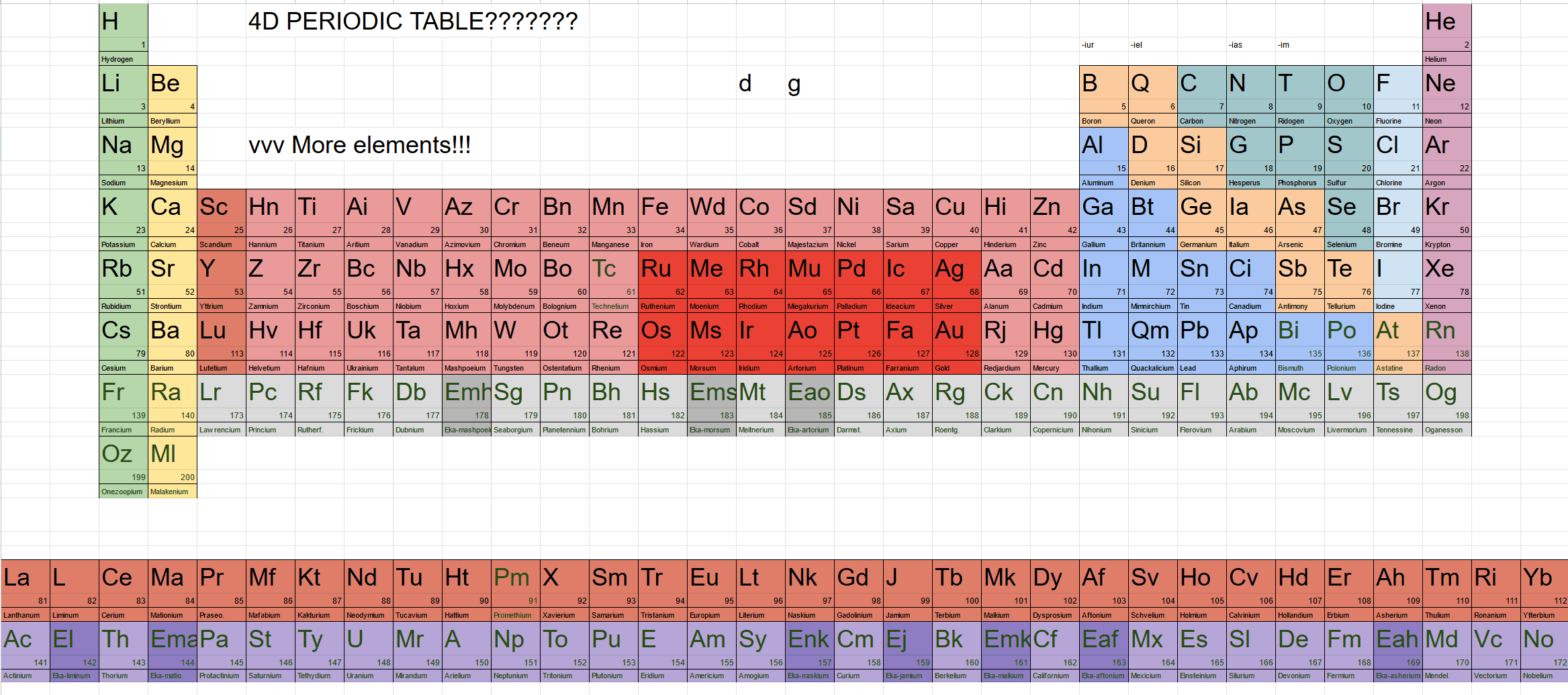

从这个周期表来看，四维元素的周期表跟三维的很像，只是主族多了两列，副族多得更长了，而锕系、镧系更加长得不得了，这是$p$、$d$与$f$轨道数量更多导致的。

常见化合物

对于四维世界的碳原子的东西最外层只有5个电子，充满最多要10个，所以还多了一种烃。我将碳碳单键的烃还是叫烷烃，它是正五胞体构型的分子，为sp⁴杂化，双键的结构我选择了“烜”(xuan)这个字，它读音切于烷与烯，表示介于烷与烯之间的新烃类，它的分子构型是正四面体型，垂直于四面体胞的两侧有两个未参与sp³杂化的孤电子对。三键的结构则反而类似平面正三角形的烯类，采用sp²杂化，它有两对互相垂直的孤电子对，位于正三角形绝对垂直的平面上。最后直线型的是四键的乙炔，为sp杂化。

刚才我们看到了五价的碳元素，除了一价、二价、三价的氟、氧、氮元素，四维最大的亮点是在碳和氮之间还多了一种四价元素，我最先称之为“砃”，但后来突然想到含氮的化合物一般都叫“硝”，干脆把“硝”作为新元素的名称（该元素在Higher Space论坛上称为N，氮元素才称为T），它的化合价为四价，而但元素的化合价。为什么说它像氮而不是碳呢？因为它最外层有6个电子，还差4个电子达到稳定的全充满结构，最多成四个键，还剩下一个本来就充满的孤电子对，这一点上确实更像氮而不像碳。根据价电子互斥理论我们还能够预测水分子是折线形、氮氨是三角锥形、硝氨是四面体锥形、甲烷是正五胞体形……

真是如此吗？

本来我是打算继续探究苯、氨基酸、脱氧核糖核苷酸等更复杂的有机物的结构的，但我突然想到，四维具有的双旋转效应会不会让电子的自旋状态不再是只有上下两个方向呢？如果是那样，刚才的元素周期表就全部是错的，刚才的分子结构也全错了。为了搞清楚四维电子到底怎么自旋，我们将深入到量子场论中描述电子运动的狄拉克方程，去探究电子自旋的秘密。这部分对物理学与数学的要求比较高，我将它放入选读中，读者完全可以跳过直接看结论。

选读：自旋与泡利矩阵

三维世界中电子的自旋

我们的世界中，电子的自旋一直都是个神秘的现象。类似地球绕太阳旋转有公转自转，电子分别有轨道角动量和自旋角动量。轨道角动量就是电子的波函数在绕着原子核旋转（p及以上的轨道都有），自旋角动量则像是电子的自转。电子是基本粒子，本质上就是一个点，如何感知它在自转呢？探测带电物体自转产生的磁矩即可。

在量子力学中，粒子的位置$r$和动量$p$不能同时确定，而轨道角动量$l=r\times p$正好由两个“矛盾”的量组成，导致测量角动量时只能同时测量到角动量的总大小和某个方向上的角动量分量但不能同时测量角动量的所有分量，因为它们也会像同时确定位置和动量那样变得不确定。自旋角动量就更奇怪了：它除了跟轨道角动量有一样的规律（即能同时测量哪些量、不能同时测量哪些量），其它就跟位置空间上的波函数没有任何关联了，类似于地球的自转朝向跟其在宇宙中的位置是没关联的。因此除了空间波函数，还需要专门引入一种“内部空间”的量子态来描述自旋状态。

电子自旋的量子态到底是什么样子的呢？大家都知道电磁场是矢量场，它也有轨道角动量和自旋角动量：当我们旋转整个空间时，肯定是电磁场在空间中的位置（对应轨道角动量）跟箭头的指向（对应自旋角动量）一起旋转，而不会单独旋转其中之一。电子的自旋也类似于向量箭头，它们都遵循在旋转变换下也跟着变换的这个规则。通过研究旋转群的群表示论可以得出：要想满足旋转变换规则，要么这个东西像个标量（即与旋转无关，一直不变），要么像个向量（像电磁场那样），要么像一些高阶张量（比如引力子像对称二阶张量，类似一个椭圆形，旋转180度后就复原），还可能像旋量——我们在几何代数中介绍过的东西——它在空间旋转360度后符号会反向。人们发现电子的自旋正遵循旋量的变换规律。

当时的人们是通过原子光谱中出现两条很近的光谱谱线的现象来得知电子的自旋磁矩的，并且也说明了电子的自旋角动量分量只能取离散的两个值。科学家泡利弄出了三个“泡利矩阵”，将泡利矩阵乘上$\hbar/2$后就是自旋角动量的算符。$\sigma_z$已经是对角矩阵了，说明这两个量子态正好就是$z$轴自旋角动量的本征态。现在看起来$z$轴好像很特殊，其实不然，我们将介绍旋量的旋转变换规则，它允许我们把任意方向都旋转到$z$轴上去从而消灭特殊性。
$$\sigma_x=\begin{pmatrix}0 & 1 \\ 1 & 0 \end{pmatrix}$$$$\sigma_y=\begin{pmatrix}0 & -i \\ i & 0 \end{pmatrix}$$$$\sigma_z=\begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix} $$很容易验证着三个矩阵$\sigma_x$、$\sigma_y$、$\sigma_z$都满足自身平方为单位矩阵，任意两个矩阵相乘则得到第三个矩阵，最多差一个系数$\pm i$，这意味着泡利矩阵之间的乘法完全跟几何代数中三维单位正交向量之间的内积与外积对应，或换句话说，泡利矩阵之间的乘法与三维单位正交向量的几何积完全对应。三个泡利矩阵相当于三维空间中的三个基向量，如果旋转整个空间，那么看成三个向量的三个泡利矩阵也应该会被旋转。数学上说泡利矩阵其实是几何代数的复矩阵表示。现在知道了泡利矩阵在旋转中怎么变，我们就能够写出任意方向上的自旋角动量分量算符了，它们都是这三个泡利矩阵的线性组合，就像一般的三维向量都是三个单位正交基向量的线性组合那样。

四维时空中电子的自旋

现在就开始上四维可能还很难，先在熟悉的3+1维时空中热热身吧：考虑相对论的电子自旋波函数方程。量子力学中波动方程的核心是，波动的时间频率正比于波的能量$\mathrm E$(或哈密顿量$\mathrm H$)，即$$i\hbar{\partial \psi \over \partial t}= \mathrm H \psi$$波动的空间频率正比于波的动量$\mathrm p$，即$$i\hbar{\nabla \psi }= \mathrm p \psi$$如果按$\mathrm H={p^2\over 2 m}$代入则得到类似牛顿力学的经典薛定谔方程。如果把方程两边“平方”，代入相对论中的能量关系$\mathrm H^2=\mathrm p^2c^2+m^2c^4$则得到Klein-Gordon方程：$$\hbar^2({\partial^2 \over \partial x^2}+{\partial^2 \over \partial y^2}+{\partial^2 \over \partial z^2}-{\partial^2 \over c^2\partial t^2})\psi= m^2c^2\psi$$然而它是二阶方程，并不能像薛定谔方程那样给定一个初始的波函数就能直接模拟它的演化，还需要提供额外的条件，比如波函数演化的“初速度”才能唯一求解，除了解不能唯一确定，Klein-Gordon方程还有因平方造成的可以取“负能”的问题……为了解决这些问题，狄拉克将Klein-Gordon方程开方，假设$\mathrm H = c(\alpha_x\mathrm p_x+\alpha_y\mathrm p_y+\alpha_z\mathrm p_z+\beta mc^2)$是关于时空分量的一阶导，得到了狄拉克方程。由于$\mathrm H$中仅含空间方向上的偏导数，没把时空对等，我们在方程两边同时乘上$\beta^{-1}$，把对时间的偏导数项移过来整理得到$$i\hbar(\gamma_x\partial_x +\gamma_y\partial_y +\gamma_z\partial_z - \gamma_t\partial_t)\psi=mc\psi$$这些待定系数$\gamma_i$叫做狄拉克矩阵。为了让开方运算能够顺利进行，方程中的一次项的待定系数必须要是矩阵而不能是简单的数字，且矩阵之间的乘法运算必须要遵守刚才说到的几何代数乘法规则：因为平方后不存在交叉项，不同的$\gamma_i$与$\gamma_j$相乘需要满足负交换律才能抵消掉，且自身与自身相乘正好对应Klein-Gordon方程的那些二阶偏微分项的系数，如果使用几何单位制（光速$c=1$），它们正好是时空度量下各单位向量的平方，即完美对应四维时空中的几何代数版本——$e_x^2=e_y^2=e_z^2=1$，但$e_t^2=-1$。

要满足三维时空的几何代数乘法法则，这些狄拉克矩阵至少得是4维的复矩阵，波函数$\psi$的四个分量分别对应电子与反电子（正电子）的两种自旋量子态。

四维世界中电子的自旋

其实我们稍加改写就能将四维时空中的狄拉克矩阵转变成四维纯空间几何中的“泡利矩阵”。四维时空中的几何代数中$e_t^2=-1$，即狄拉克矩阵中有一个的平方是负的单位阵。我们现在希望构造所有四个矩阵的平方都是单位矩阵的代数，经过一番尝试，不难得到以下的一组解：
$$\sigma_x=\begin{pmatrix}0&0&1&0 \\ 0&0&0&1 \\ 1&0&0&0 \\ 0&1&0&0\end{pmatrix}$$$$\sigma_y=\begin{pmatrix}0&0&i&0 \\ 0&0&0&-i \\ -i&0&0&0 \\ 0&i&0&0\end{pmatrix}$$$$\sigma_z=\begin{pmatrix}0&0&0&i \\ 0&0&i&0 \\ 0&-i&0&0 \\ -i&0&0&0\end{pmatrix}$$$$\sigma_w=\begin{pmatrix}0&0&0&1 \\ 0&0&-1&0 \\ 0&-1&0&0 \\ 1&0&0&0\end{pmatrix}$$

因为角动量是2-向量，因此不妨假设$\sigma_a\sigma_b$乘上一个系数后就是自旋角动量算符在坐标面$ab$上的分量。注意三维的泡利矩阵利用了霍奇对偶（比如$\sigma_x\sigma_y=i\sigma_z$）因此只出现了向量。计算这些代表2-向量的矩阵后发现，有两组矩阵确实是对角化的，这说明我们找到了一些四维电子的自旋本征态：
$$\sigma_x\sigma_y=i\begin{pmatrix}-1&0&0&0\\0&1&0&0 \\ 0&0&1&0 \\ 0&0&0&-1 \end{pmatrix}$$$$\sigma_z\sigma_w=i\begin{pmatrix}1&0&0&0\\0&-1&0&0 \\ 0&0&1&0 \\ 0&0&0&-1 \end{pmatrix}$$它们对应着$xy$与$zw$方向上的自旋角动量。从上面的结果可知它们都是二值的，它们都是对角阵，说明这两个算符是对易的，保证了我们可以同时测量其上的值：这四种量子态的$xy$与$zw$方向上的角动量分量都只能是$\pm\hbar/2$，类似我们熟知的三维空间中电子那样。

跟讨论轨道角动量的角量子数类似，设$\sigma^{+}=(\sigma_x\sigma_y+\sigma_z\sigma_w)/2$、$\sigma^{-}=(\sigma_x\sigma_y-\sigma_z\sigma_w)/2$，这两个算符对应着测量电子自旋角动量算符的左等角旋转分量$(e_{xy}+e_{zw})/2$与右等角旋转分量$(e_{xy}-e_{zw})/2$。我们发现这两个矩阵是分块的，且说明了电子的自旋可进一步分为左等角“上”、“下”和右等角“上”、“下”四种态。上一篇文章中我们绘制的各总角量子数下角动量分量仅能取某些特定值的表，现在是时候也把电子自旋加进去了：

上图中网格的中心对应所有角动量分量为0的态，灰色网格纵横方向对应$xy$、$zw$平面上的角动量分量，一格代表一个量子数（角动量对应一个$\hbar$）；蓝色网格斜着的纵横方向对应$(e_{xy}+e_{zw})/2$、$(e_{xy}-e_{zw})/2$两个分别左右等角（霍奇自对偶和反自对偶）的角动量分量，一格代表半个量子数，即角动量对应一个$\hbar/2$。

综合刚才两种角动量基底，我们能够看出电子自旋跟轨道角动量性质截然相反：轨道角动量都是简单旋转，而电子自旋都是双旋转。如果电子自旋是简单旋转，则它不可能是本征态，只可能是叠加态，这种简单旋转态是不可观测的，因为只要对电子自旋进行测量，它就会“坍缩”至一个确定的双旋转的状态。

选读中的选读：N维世界中的电子自旋

刚才只是推导了四维世界中电子在空间部分的自旋，在时空中，它需要遵循4+1维时空中的狄拉克方程：里面的5个系数$\gamma$矩阵的乘法应该可以对应表示4+1维时空中的几何代数。
$$i\hbar(\gamma_x\partial_x +\gamma_y\partial_y +\gamma_z\partial_z +\gamma_w\partial_w- \gamma_t\partial_t)\psi=mc\psi$$
现在的$\gamma$矩阵是几阶的呢？数学上可以推导，对于$m+n$维时空，它的几何代数的复矩阵表示至少要是$2^{\lfloor{m+n\over 2}\rfloor}$阶的，其中$\lfloor . \rfloor$是向下取整符号。也就是说，4+1维时空的$\gamma$矩阵也是四维的。

对于二维世界也可以套上面的维度公式。二维空间中泡利矩阵的阶为$2^{\lfloor{2\over 2}\rfloor}=2$，正好对应电子自旋只有顺时针和逆时针两个方向，它们的狄拉克方程对应2+1维空间中的几何代数，其矩阵表示阶数$2^{\lfloor{(2+1)\over 2}\rfloor}$由于取整还是2。如果有五维世界，可以算出电子的自旋还是4种状态，但到了6维就有8种状态了：我们把坐标面两两分组，形成三个互不影响的绝对垂直的角动量分量，它们上面各有“上”“下”两种自旋态，排列组合下来总共就是8种。对更高维空间随维度增加的规律就是，每逢偶数维，电子的自旋态就会翻倍，逢奇数维不变，更多详情请参考维基百科词条Higher-dimensional gamma matrices。

修正：四维周期表最终版

现在可以对四维原子中的电子自旋下结论了，它确实有左等角“上”、“下”和右等角“上”、“下”四种态，且自旋都是1/2，电子还是费米子。（2025.05更正：其实四维原子中的电子自旋状态数量不能直接推出，必须根据四维世界中的“实验”来确定：4denthusiast提出了一种只有左等角“上”、“下”两态的世界观设定，虽然只有左旋没有右旋很奇怪，但我们真实世界也有宇称不守恒这种怪事。本Blog默认左右手电子均存在且数量几乎相等）根据泡利不相容原理，同一状态下的费米子所有的量子数不能完全相同，因此一个原子轨道能塞4个电子，相比与二维和三维一个轨道两个电子，周期表的长度会翻倍：

1. 每层的s轨道有1个，能填4个电子；
2. 每层的p轨道有4个，能填16个电子；
3. 每层的d轨道有9个，能填36个电子；
4. 每层的f轨道有16个，能填64个电子。

这个周期表非常庞大。我跟网友宁宁一起搓出了一张完整7行的拥有396个元素的周期表（找那么多金字旁的字真是个挑战）。由于从d副族开始就很长了（36列），更不要说锕系镧系（64列），我当时想了两种排版方式：第一种是直接类似三维世界的元素周期表排版，第二种是将d副族就像锕系镧系那样单列出来，然后将锕系镧系的每行也在中间换行。但后来发现第二种太丑了就没采用，第一种虽然很长，但排出来还是很漂亮的：

这里提供以下几种格式的四维元素周期表：

• 电脑端推荐浏览器网页单独在线查看（注意手机端默认字体似乎显示不全所有字）；
• 下载PDF文档；
• 下载png图片；
• 下载可编辑的Excel版，建议同时安装简体Chemical4D字体文件。

顺带提一下周期表的设计思路：

• 参考Higher Space论坛上的元素周期表将其长度翻倍，并将元素列数乘以二填入偶数序数格子中（碱金属、卤素等少数元素例外），奇数号元素为四自旋态电子额外增加的，一般参考前后两个元素的名称或其性质命名，或参考纪念名人（如“El 鏂”纪念数学家欧拉），也有随机或玩梗的。
• 所有三维世界中的元素均在该表中对应位置出现，Higher Space论坛上的元素周期表也遵守了这个规则。
• 选字时均使用的是Unicode中收录的汉字，其中有些字只有繁体版本，我通过编辑字体将其简化。
• 四维生物在绘制这些四维周期表时是在三维纸张上面进行的，表格也应该是3D的，读者可以思考一下具体怎么设计。

能量最低原理与洪特规则特例

三维世界中，填入轨道的电子首先是顺着方向一个一个填，然后再成对反着填。这是因为电子自旋方向一致时能量最低，可以形象想象成电子都是一个个的磁铁，它们会自发保持方向一致。当电子太多了都顺着填要违反泡利不相容原理了，它们才会反着挤到同一个轨道中。

四维世界中我们用四个方向的箭头来代表四种方向的自旋。《四维世界（八）：地理与导航》中已经分析过，左手跟右手的等角双旋转磁偶极子相互之间是不会有任何相互作用的。因此我们的箭头之间也是相差90度，它们之间的相互作用能量在取向一致与相反中间。电子会优先以同种手性同种朝向填满所有空轨道，然后是填入另一种手性同种朝向，然后再填入剩下两种自旋方向的电子。(25.04.10修正：左手与右手磁偶极子之间会有相互作用，但同手性磁偶极子之间是不会有任何相互作用的，所以不会强迫箭头方向一致填入，因此填入轨道时顺序可能会很乱，具体行为已超出我预测能力之外，姑且仍假设电子们优先占据尽可能多的格子。)

洪特规则特例告诉我们，当电子层处于全充满是最稳定的，半充满也是比较稳定的状态。我们可以假设在四维空间中，电子层中的电子数在1/4充满与3/4充满的状态下仍有一定的稳定性，但这两种状态还是没有半充满与全充满稳定。这导致了一些副族元素的电子排布不再严格按照能级交错的顺序填电子，比如铜的电子排布是3d³⁶4s²(3d全充满，4s半充满)，而不是3d³⁴4s⁴，跟三维世界的情况是相似的。

常见元素的性质

由于电子数翻倍了，我们很自然地就可以假设通常情况下共价化合物不再是共享2个电子成键，而是需要4个电子来成键了。以周期表第一行的氕、氘、氚元素为例，它们可以形成下面这些化合物，从而都达到稀有气体氦的核外电子排布。

这里我借鉴了氢的同位素的名字来为一周期的三种元素命名，它们的单质密度都比空气轻，统称为“氢素”。氕的单质是H₄，因为每个氕原子只有一个电子，需要四个凑到一块才能凑够四个电子形成稳定结构。我们看到现在的化学键可以是多个原子之间共同成键，其成键方式比三维的情况丰富得多。从第二周期开始，价电子就有一个s轨道加4个p轨道5个轨道共20个电子了，非金属一般都倾向于得到电子形成氖原子外的核外电子结构。

由于元素周期表长度翻倍，这些元素可能构成的化合物种类排列组合下来要比三维世界中多得多，大概三维世界中需要一小节讲得内容对应到四维世界就是一章。下篇文章我们将探究假想的四维世界中的化学会是什么样的，并跟随探险家的脚步一同前往四维类地行星，分析地表大气成分及各种四维矿石的晶体结构。

思考题

本文最后列出了一些问题留给读者思考一下，参考答案将在下篇文章揭晓。（免责申明：由于都是强行假设，答案仅供参考和娱乐，不代表正确，别把我当成民科喷就行。。。）

1. 氕（H：1s¹）与氧（O：1s⁴2s⁴2p¹²）能够形成哪些分子，氘（D：1s²）与氧呢？
2. 四维世界的类似“水”的分子的结构有哪些可能？
3. 四维世界的类似“苯”的分子的结构有哪些可能？
4. 氚（T：1s³）的单质最可能的结构是什么样的？
5. 碳单质（C：1s⁴2s⁴2p⁶）在氧气（O₂）中不完全燃烧与完全燃烧分别生成的不同氧化物产物的结构是什么样的？