四维世界(十二):物质结构
上期我们探讨了四维元素周期律设定,这次来看看物质结构,并毫无根据地大胆预估一下它们的性质(我不是学化学的,欢迎大家对所有内容提出异议)。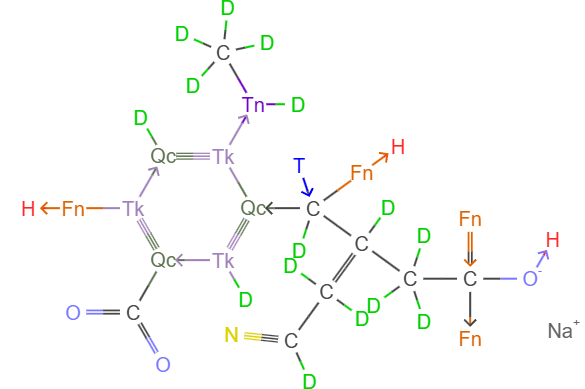 当我正在继续写这部分内容时,网友KWOK Chun给我分享了一个叫《对称4D化学》的Google在线文档(该文档任何人可编辑,欢迎大家一起编辑完善),里面的四维化学设定周期表设定跟我的完全相同的,只是元素命名上不同,本文快写完时我还看到了专门讲四维化学并尝试定量计算分析的4denthusiast’s Blog,他们试图从基础粒子物理出发建立更严谨的四维基础物理体系,我也将分享一些精彩的内容。
当我正在继续写这部分内容时,网友KWOK Chun给我分享了一个叫《对称4D化学》的Google在线文档(该文档任何人可编辑,欢迎大家一起编辑完善),里面的四维化学设定周期表设定跟我的完全相同的,只是元素命名上不同,本文快写完时我还看到了专门讲四维化学并尝试定量计算分析的4denthusiast’s Blog,他们试图从基础粒子物理出发建立更严谨的四维基础物理体系,我也将分享一些精彩的内容。
特色内容
分子结构的表示方法
上篇文章末尾介绍了类氢元素(氕、氘、氚)之间能形成的化合物,并展示了多个原子共同凑齐4个电子来填满轨道的共价键电子式。第二行的元素更多,它们能形成的化合物种类比起三维来说也可能多几个数量级。我们先系统来研究一下如何写出合法的分子结构的电子式,然后再列举一些可能存在的分子结构。
电子式
写电子式时要达到稀有气体稳定结构,第一行元素需要遵守四电子规则,第二行需要遵守二十电子规则。下面给出了差一、二、三个电子达到二十电子的氟(F)、氲(Fd)、氛(Fn)三个元素参与形成的一些分子的电子式。
结构式
四维原子电子式书写很麻烦,需要更简洁的结构式。四维结构式的规则最好要能检验各原子是否达到稀有气体稳定结构,此外还要检验那些共用电子的每个轨道里电子数量是否为4。经过不断尝试,我设计出了一种比较实用的结构式表示方法:
- 对于离子,直接标上电荷即可。对于共价键的每一个轨道则遵循下面的规则:
- 若一个原子提供了2个电子,则用一根实线表示;
- 若一个原子提供了1个电子,则用指向该原子的带箭头线段表示,提供了3个电子,则用背离该原子的带箭头线段表示;
- 若一个原子提供了4个或0个电子(配位键),则用背离或指向该原子的带双箭头线段表示,亦可按前两种情况画线,并通过标记多余形式电荷的方式记录少计的电子数。
- 一个轨道可被多个原子共用,它们给的电子数可能都不一样,分叉出来的线段类型也可以不同。用实心小圆点表在分叉处表示轨道。如果只有两原子共用该轨道则无分叉,小圆点可省略,并把箭头拉通。
下面给出之前展示的几个分子的电子式对应的结构式版本:这些箭头很好地指示出了成键电子的来源。
当我完成结构式的设定后才看到《对称4D化学》中早就提出了类似的结构式画法,只是一些符号上存在差异:两边各提供2个原子叫正键,还是用一根线表示;各提供1个和3个电子叫客键,在提供三个电子那边画一个竖线;配位键(他们建议改成叫“从键”)则用正常的单箭头表示。《对称4D化学》的元素命名出现了一些我也用过的相同的字,比如他们的氤(Ae)、氲(Az)、砃(Dy)对应我的硝(E)、氮(N)、氛(Fn),而我的氤(Ny)、氲(Fd)、砃(Dd)对应他们的氮(N)、氱(El)、锴(Cr)。下面给了一些例子:左边是我(本文默认)的写法,右边是同样物质在《对称4D化学》中的写法。
稳定结构判断
如何判断结构式是否符合稀有气体稳定结构和每个轨道4电子数的这两个要求呢?下面给出结构式校验规则。
- 首先引入键数的概念。每个原子或轨道都有键数,计算方法为:正常的实线为单($1$)键,有一个指向自己的箭头就额外增加$0.5$键,背离的减少$0.5$键;
- 对于核外差$k$个电子才到稀有气体结构的原子,其成键总数应为$(k+e)/2$,其中$e$为该原子上标的形式电荷数,且整个分子的总电荷数应为$0$;
- 对每个共用的轨道计算其键数应恒为$2$。
- 由于轨道数限制,对于一周期元素最多只能有一根线与其相连,对于二周期元素最多只能有$5$根线与其相连。
从第二条规则我们可得知,正常没有标电荷的情况下,氕(H)需要成1.5键,氘(D)成1键,氚(T)成0.5键;氟(F)成0.5键,氲(Fd)成1键,氛(Fn)成1.5键,大家可自行检验上面图中的各原子键数。
最后有个小推论:一般来说一个电中性的分子中,奇数原子序数的原子个数一定为偶数。当然不排除有例外,比如类似于三维世界中的一氧化氮分子那样有未成对电子显顺磁性,这些现象需要分子轨道理论解释。这里我再次申明一下,包括分子轨道理论在内本文的内容完全是无根据的类比,“实际”的四维物质的稳定性结论可能会大有不同。后面我们将介绍可能的四维粒子物理与四维计算化学的尝试。
选读:分子轨道理论 [展开/收起]
多中心键与富电子化合物
多中心键即多个原子共用电子形成的键,可以用来解释缺电子分子,比如乙硼烷、三氯化硼等分子结构,四维世界中的氕气分子H4就是一个典型的缺电子分子。在上篇文章留的思考题中提到了氚的单质会是什么结构。氚有3个电子,还缺一个电子,它只能组成富电子分子:可以四个氚共用12个电子形成三个填满的成键轨道。还有网友提出其实还可以直接形成双原子分子,它们只需要各自出一个电子来共用,这样每个原子都有四个电子了。这样的结构合法吗?分子轨道理论认为键的本质其实不只是共享电子,一般两原子轨道之间重新叠加形成两个分子轨道,一个轨道能量高(反键轨道),一个轨道能量低(成键轨道),电子都去填能量低的轨道填满,让能量高的轨道空着,这样的整体整体能量比单独的两原子轨道里各一个电子能量低,所以更稳定。四个氚原子有四个原子轨道,它们线性叠加组合也还是四个分子轨道,类似于线性空间中换了一个坐标基底而保持维数不变。它们共享的是轨道,而不是电子,电子只能填入轨道,双原子氚分子中,想只共享2个电子而其余电子私有是不可能的,因为轨道要么叠加在一起成键,要么不成键。
富电子氟化物
六氟化硫、二氟化氙如何类比到四维呢?首先我们要搞懂三维的这些分子是如何存在的。硫本来外面有6个电子,只差2个电子,而氟是7个电子,只差1个电子,因此最简单的化合物应该是二氟化硫F-S-F。此时硫原子上还有两个孤电子。由于氟原子高度活泼,导致氟气还能继续跟二氟化硫反应:两个氟各出一个电子,硫原子的一个孤电子对再出两个电子,被三个原子共用,可以再形成一个3中心4电子键,得到四氟化硫。氟原子本来只差一个电子,形成3中心4电子键后会让氟外的电子数超过8个,所以叫富电子分子,但为何它稳定呢?这可以用带形式电荷的共振式来解释判断:下面的四氟化硫分子中虽然有个氟看起来是离子,跟其它三个不一样,然而其实不同位置上可以交替变成负离子。六氟化硫比四氟化硫还多了一对3中心4电子键,情况也类似。实际测量六氟化硫发现所有的S-F键都是等长的,说明多中心键的描述才是实际情况,可看作是这些共振式的量子叠加态构成了多中心键。共振结构可以让所有原子都符合8电子稳定结构,并且还能数出中心原子上的孤电子对数,从而根据价电子互斥理论预测其分子空间形状。
下面轮到四维了,这里我直接给出几种有意思的富电子分子:八氲化硫与八氚化磻(六氟化硫的类比,都是正十六胞体分子)、六氚化氮(正八面体平胞结构,有两个孤电子轨道在法线两侧)、六氚化碳(一个孤电子轨道,导致分子为4,3-双锥形少一个三角形上的顶点的形状)、十九氟化碘(七氟化碘的类比)。下图给出了两个比较复杂的分子结构,请大家自行推断其它没给出结构的分子的共振结构式。提示:1. 我们稍后马上介绍四维价电子互斥理论预测分子的具体形状;2. 上面这些分子可以在Chem4D分子库中查到,具体操作方法见这里。
顺磁性
在三维真实世界中,氧气分子并不是双键而是三键结构,这来源于分子轨道理论的计算,且三键中有未成对的电子,它产生的磁矩不能被抵消,导致液氧能被磁铁吸引,这就是顺磁性。《对称4D化学》中也画出了氧气分子的分子轨道能级图,但没给出具体结论。我给出的预测结论是从3.5价的磴开始到1.5价的氛,它们若能形成双原子分子可能就都是四键结构且有未成对电子。全充满的轨道由于泡利不相容原理一定是四个不同磁矩且总磁矩为零,只有有未成对电子才可能在外磁场方向中被磁化得保持取向一致,因此四维氧气分子也具有顺磁性。排除掉磴可能是固体晶体、氛气是四原子分子,只有氮气、氤气和氧气三种单质是四键结构具有顺磁性,此外我猜还可能有一氧化氮、一氧化氛等顺磁性化合物。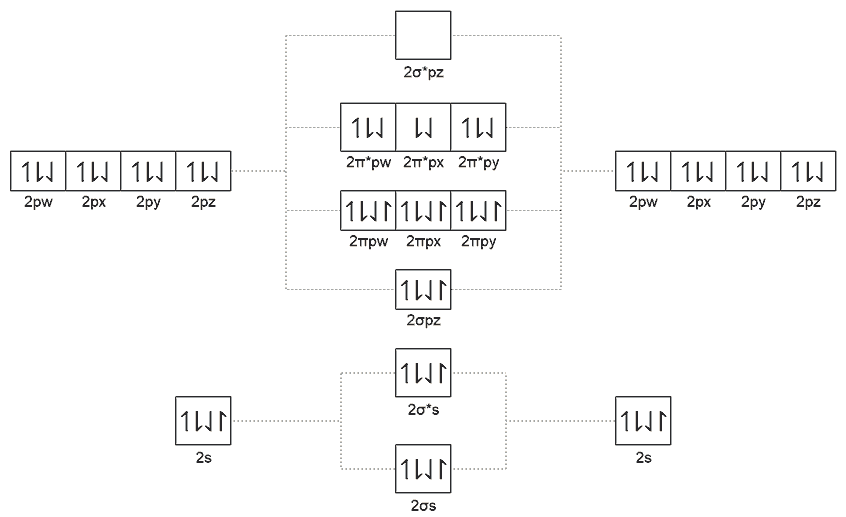
注:磁性可分为顺磁性、反磁性(或抗磁性)、铁磁性三类:顺磁性物质的磁性不强,无法自发形成取向一致的磁畴,因为会被热布朗运动打乱。铁磁性则是顺磁性非常强的物质,强到可以形成稳定的磁畴。没有顺磁性的物质就是反磁性的,它们对磁场几乎不响应。铁是过渡金属,d轨道电子的能量情况很复杂,允许有未成对电子的稳定结构从而让铁磁性变得可能,对于四维化学也同理,但具体哪些物质磁性强就无法得知了。
过渡金属离子与配位场理论
三维过渡金属离子价态与单纯的原子不同,通常离子周围都有很多配合物,比如铜离子在溶液中都是以水合离子的形式存在。配位场理论认为,这些周围的配位原子会影响各d轨道的能级,比如正八面体配位场中原来能量相同的5个d轨道能级分裂为两种不同的能级,三个低能轨道和两个高能轨道,如果相差的能量大于了克服自旋方向不一致的能量,这时离子可能优先填满能量最低的三个轨道,再去填剩下两个轨道,于是除了洪特规则下的0、5、10电子稳定外,3、6、8电子也是稳定的。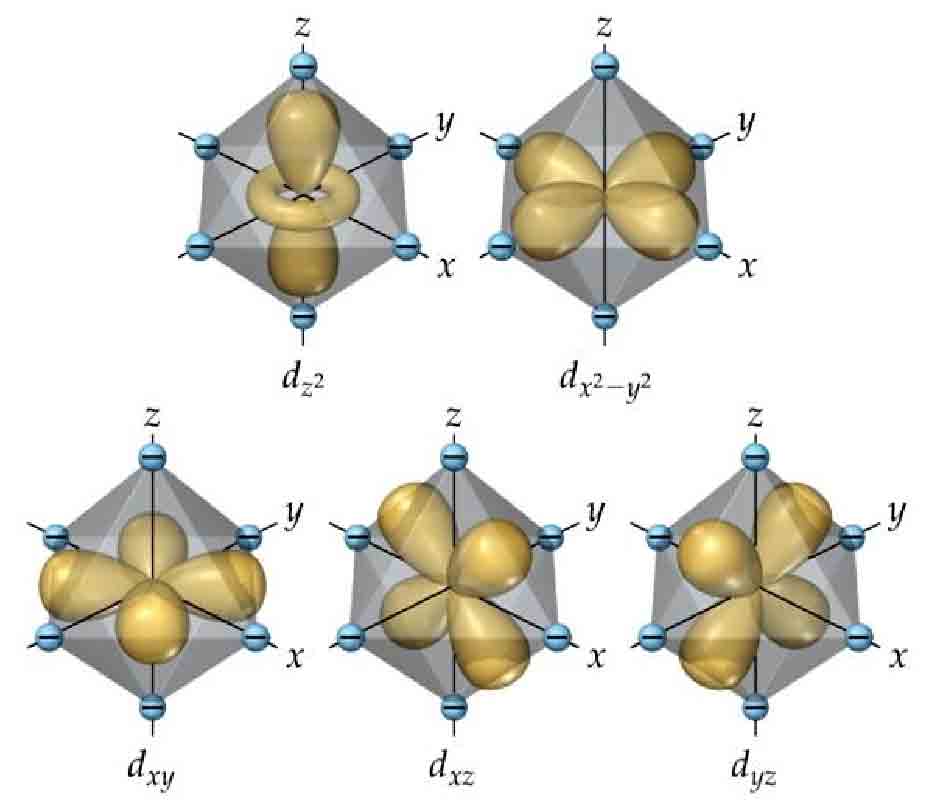 过渡金属离子的情况相当复杂,还有姜-泰勒效应、正四面体配位、正方形配位等等,导致同种金属离子的价态非常丰富,不做定量计算分析是无法简单通过规则来确定离子的常见化合价的。
过渡金属离子的情况相当复杂,还有姜-泰勒效应、正四面体配位、正方形配位等等,导致同种金属离子的价态非常丰富,不做定量计算分析是无法简单通过规则来确定离子的常见化合价的。
最常见的正八面体配位场的四维类比——正十六胞体配位场中,d轨道能级分裂为6+3结构:3个轨道能量低、6个轨道能量高。四维空间中有Hopf基与极坐标基两种情况,这两种基下结论是一样的:
- 超球轨基下面的$xy$、$xz$、$xw$、$zw$、$yw$轨道跟三维的类似,轨道的“花瓣”指向轴之间,不与轴重合;$x^2+y^2+z^2-3w^2$、$x^2+y^2-2z^2$分别迎头碰上$z$、$w$轴上的离子,$x^2-y^2$则碰上$x$、$y$轴的离子,故这三个轨道能量更高。
- Hopf基下同样也有$xy$、$xz$、$xw$、$zw$、$yw$六个不与轴重合的轨道,是一样的;$x^2-y^2$碰上$x$、$y$轴的离子,$z^2-w^2$碰上$z$、$w$轴的离子,$x^2+y^2-z^2-w^2$在xy平面与zw平面上密度最大,同时与正十六胞体所有离子相碰,故这三个轨道能量更高。
按照洪特规则,d轨道电子数取0、9、18、27、36是全半充满的稳定结构,能级分裂后导致这些d轨道电子数也是稳定的:6、12、18、24、27、30、33、36,因此四维过渡金属可能也会像三维那样有多种价态,但具体的稳定性需要定量计算才知道。
有了结构式就能方便快捷地描述分子结构了,然而别忘了分子是在四维空间中而不是在二维或三维的纸面上,下面我们来研究它们的空间结构。
价电子互斥(VSEPR)模型
价层电子对互斥理论认为分子或离子的几何结构主要决定于与中心原子相关的价电子对之间的排斥作用使得电子对尽可能分散分布让能量最低,电子对既可以是成键的,也可以是没有成键的孤对电子。三维空间中,电子对数量对应的几何形状见下图: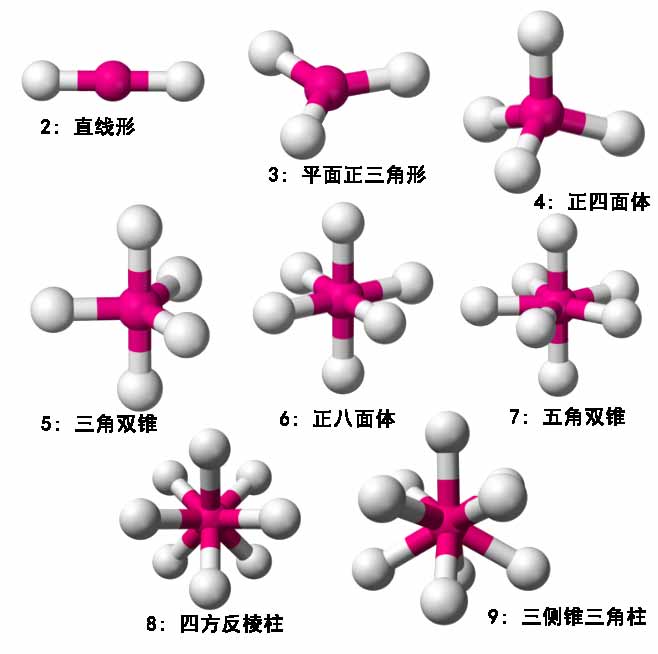
这里解释一下四方反棱柱:按理说8个电子对最对称的该是正方体的八个顶角,然而将正方体的底面旋转45度与顶面错开后显然能量还会再低一些,故采取该模式;三侧锥三角柱比较复杂,可参见维基百科的介绍。
四维空间中的情况又是怎样的呢?《对称4D化学》中他们也给了初步猜测。我在Tesserxel平台搭建的VSEPR“仿真”测试中观察发现:
- 2~4个电子对(其实是四个电子形成一组,只是我们还是习惯称为“对”)时其实跟三维空间的是一样的,增加到5个电子对时才会把电子挤向第四个维度,形成正五胞体分布;
- 6个顶点的图形我之前跟《对称4D化学》都想的是3,3-双锥形,然而模拟发现其实是类似三角双锥那样的正四面体双锥;7个顶点时对应3,4-双锥形(也可以看作三角双锥双锥)、8个顶点对应4,4-双锥形(即正十六胞体,或正八面体双锥)、9个顶点对应4,5-双锥形(五角双锥双锥);
- 到第10个顶点后,分子形状既不是5,5-双锥形,也不是我之前想的一种类似四维“二十方”晶系的结构,而是一种分层结构——第一层为正四面体4个顶点、第二层为中心原子、第三层为第一层正四面体棱的位置对下来的六个顶点形成正八面体;
- 11个顶点的图形我没看出什么规律,隐约觉得可以分成第一层三角双锥、第二层中心原子、第三层变形的三棱柱结构;12个顶点的图形则是一种类似于反四棱柱那样的扭转的正八面体柱,再往后面几乎很难看出具体形状规律了。
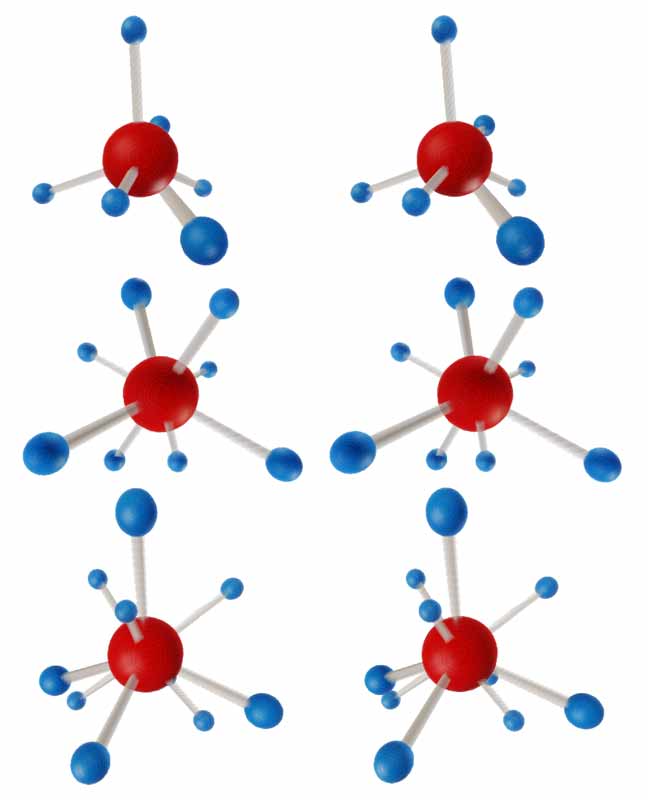
注:该“仿真”程序中,排斥能量按照四维世界“真实”的立方反比力衰减、平方反比势能衰减的规律计算,若按三维的平方反比力衰减、反比势能衰减计算,某些分子的最低能量形状可能会有所不同。
说完了一大堆理论,下面来看看具体的四维分子。
常见无机化合物
非金属氢化物
在我们的世界,氢与二周期非金属的常见化合物只有氟化氢、水、氨、甲烷这几个:(硼烷是用多中心键才能解释的缺电子分子,不太常见我们暂时忽略它)
| 化学式 | 名称 | 孤电子对 | 氢键 | 常温常压下 | 极性 |
|---|---|---|---|---|---|
| HF | 氟化氢 | 3 | 1 | 气体 | 极性 |
| H2O | 水 | 2 | 2 | 液体 | 极性 |
| NH3 | 氨 | 1 | 1 | 气体 | 极性 |
| CH4 | 甲烷 | 0 | 0 | 气体 | 非极性 |
而四维世界中,氢有3种,二周期常见的非金属元素也翻了三倍,它们的组合情况多得多。下面列举了部分有代表性的化合物。其中名称是我自己瞎定的规则取的:共价轨道数从1至5分别叫“x化x”、“x水”、“x氨”、“x氠”、“x烷”,这种命名的好处是孤电子数和分子几何构型跟名称直接对应。然后氧水可简称为水、氮氨简称氨、硝氠简称氠、碳烷简称烷。与另一个原子共用轨道的两个氕叫“泾”,默认都是尽可能多连氘(D),其次是氕(H)最后是氚(T)。
我猜测含泾(-H2)的化合物都是很强的酸,它极易电离出氢离子变成-H-和H+。在三维世界中(感谢网友宁宁的提醒),甲烷在超强酸性环境下可以得到一个质子变成含有三中心二电子键的甲鎓离子(CH5+)。
刚才只是选择了一些有代表的化合物,这些组合到底一共有多少呢?我列出了69种从碳到氟的单原子氢化物。由于不知道“真正”的四维物质的化学稳定性,我们只能认为所有的符合稀有气体结构的分子都是稳定的,而且电负性大的原子还会跟氢形成一些用分子轨道理论解释的富电子化合物:如直线形的氟化氘、一氲化二氚,平面三角形的氟化氚和平面正方形的四氚化氧。类似乙烷、丙烷那些双原子、多原子氢化物,将放在后面有机物中再细说。
| 化学式 | 名称 | 孤电子轨 | 氢键 | 常温常压下 | 极性 |
|---|---|---|---|---|---|
| HF | 氟化氕 | 4 | 1 | 气体 | 极性 |
| DF2 | 氟化氘 | 10(富电子) | 0 | 气体 | 非极性 |
| TF3 | 氟化氚 | 15(富电子) | 0 | 气体 | 非极性 |
| H2Fd | 氲水 | 3 | 2 | 液体 | 极性 |
| DFd | 氲化氘 | 4 | 1 | 气体 | 极性 |
| T2Fd | 一氲化二氚 | 4(富电子) | 2 | 液体 | 非极性 |
| H3Fn | 氛氨 | 2 | 2 | 液体 | 极性 |
| HDFn | 氛水 | 3 | 2 | 液体 | 极性 |
| DFn2 | 氛化氘 | 7 | 1 | 气体 | 极性 |
| TFn | 氛化氚 | 4 | 1 | 气体 | 极性 |
| H4O | 氧氠 | 1 | 1 | 气体 | 极性 |
| H2DO | 氧氨 | 2 | 2 | 液体 | 极性 |
| D2O | 水 | 3 | 2 | 液体 | 极性 |
| HTO | 氚水 | 3 | 2 | 液体 | 极性 |
| T4O | 四氚化氧 | 3(富电子) | 3 | 液体 | 非极性 |
| H5Ny | 氤烷 | 0 | 0 | 气体 | 非极性 |
| H3DNy | 氤氠 | 1 | 1 | 气体 | 极性 |
| HD2Ny | 氤氨 | 2 | 2 | 液体 | 极性 |
| H2TNy | 氚氤氨 | 2 | 2 | 液体 | 极性 |
| DTNy | 氤水 | 3 | 2 | 液体 | 极性 |
| NH6 | 泾氮烷 | 0 | 0 | 气体 | 弱极性 |
| NH4D | 氮烷 | 0 | 0 | 气体 | 弱极性 |
| NH2D2 | 氮氠 | 1 | 1 | 气体 | 极性 |
| ND3 | 氨 | 2 | 2 | 液体/气体 | 极性 |
| NH3T | 氚氮氠 | 1 | 1 | 气体 | 极性 |
| NHDT | 氚氨 | 2 | 2 | 液体/气体 | 极性 |
| NT2 | 氮水 | 3 | 2 | 液体/气体 | 极性 |
| TnH7 | 二泾磴烷 | 0 | 0 | 气体 | 弱极性 |
| TnH5D | 一泾磴烷 | 0 | 0 | 气体 | 弱极性 |
| TnH3D2 | 磴烷 | 0 | 0 | 气体 | 弱极性 |
| TnHD3 | 磴氠 | 1 | 1 | 气体 | 极性 |
| TnH4T | 氚磴烷 | 0 | 0 | 气体 | 弱极性 |
| TnH2DT | 氚磴氠 | 1 | 1 | 气体 | 极性 |
| TnD2T | 一氚磴氨 | 2 | 2 | 液体/气体 | 极性 |
| TnHT2 | 二氚磴氨 | 2 | 2 | 液体/气体 | 极性 |
| EH8 | 三泾硝烷 | 0 | 0 | 气体 | 弱极性 |
| EH6D | 二泾硝烷 | 0 | 0 | 气体 | 弱极性 |
| EH4D2 | 一泾硝烷 | 0 | 0 | 气体 | 弱极性 |
| EH2D3 | 硝烷 | 0 | 0 | 气体 | 弱极性 |
| ED4 | 氠 | 1 | 1 | 气体 | 极性 |
| EH5T | 泾氚硝烷 | 0 | 0 | 气体 | 弱极性 |
| EH3DT | 氚硝烷 | 0 | 0 | 气体 | 弱极性 |
| EHD2T | 一氚氠 | 1 | 1 | 气体 | 极性 |
| EH2T2 | 二氚氠 | 1 | 1 | 气体 | 极性 |
| EDT2 | 硝氨 | 2 | 2 | 液体/气体 | 极性 |
| TkH9 | 四泾𥓬烷 | 0 | 0 | 气体 | 弱极性 |
| TkH7D | 三泾𥓬烷 | 0 | 0 | 气体 | 弱极性 |
| TkH5D2 | 二泾𥓬烷 | 0 | 0 | 气体 | 弱极性 |
| TkH3D3 | 一泾𥓬烷 | 0 | 0 | 气体 | 弱极性 |
| TkHD4 | 𥓬烷 | 0 | 0 | 气体 | 弱极性 |
| TkH6T | 二泾氚𥓬烷 | 0 | 0 | 气体 | 弱极性 |
| TkH4DT | 一泾氚𥓬烷 | 0 | 0 | 气体 | 弱极性 |
| TkH2D2T | 一氚𥓬烷 | 0 | 0 | 气体 | 弱极性 |
| TkD3T | 一氚𥓬氠 | 1 | 1 | 气体 | 极性 |
| TkH3T2 | 二氚𥓬烷 | 0 | 0 | 气体 | 弱极性 |
| TkHDT2 | 二氚𥓬氠 | 1 | 1 | 气体 | 极性 |
| TkT3 | 𥓬氨 | 2 | 2 | 液体/气体 | 极性 |
| CH10 | 五泾甲烷 | 0 | 0 | 气体 | 非极性 |
| CH8D | 四泾甲烷 | 0 | 0 | 气体 | 弱极性 |
| CH6D2 | 三泾甲烷 | 0 | 0 | 气体 | 弱极性 |
| CH4D3 | 二泾甲烷 | 0 | 0 | 气体 | 弱极性 |
| CH2D4 | 一泾甲烷 | 0 | 0 | 气体 | 弱极性 |
| CD5 | 甲烷 | 0 | 0 | 气体 | 非极性 |
| CH7T | 三泾氚甲烷 | 0 | 0 | 气体 | 弱极性 |
| CH5DT | 二泾氚甲烷 | 0 | 0 | 气体 | 弱极性 |
| CH3D2T | 一泾氚甲烷 | 0 | 0 | 气体 | 弱极性 |
| CHD3T | 氚甲烷 | 0 | 0 | 气体 | 弱极性 |
| CH4T2 | 泾二氚甲烷 | 0 | 0 | 气体 | 弱极性 |
| CH2DT2 | 二氚甲烷 | 0 | 0 | 气体 | 弱极性 |
| CD2T2 | 二氚碳氠 | 1 | 1 | 气体 | 极性 |
| CHT3 | 三氚碳氠 | 1 | 1 | 气体 | 极性 |
可能大家对这些四维元素不是很熟悉,这里再把第二行的非金属元素放出来以供查阅:
可能的酸与碱
在三维世界中,无机酸一般分为无氧酸(氢某酸)或含氧酸。到了四维,氢与氧的候选类比都会变多,无机酸种类可能会爆炸式增长。由于目前无法定量计算电离能力,我只能大致设定:氕的电离能力最强,氘次之,氚最弱,一般仅考虑氕与氘形成的酸,而氚则类似卤素不考虑电离;假设除氧元素外,氧元素右边的氛、氲元素也成参与形成酸。为什么三维只有含氧酸呢?按理说非金属性越强就越容易吸引电子,让氢更容易电离,氧和氟元素都可以。然而氟元素是1价的,它结合氢形成氢氟酸后就没机会结合其它基团了,所以没有含氟酸。到四维,这个限制被打破,下面列出了一些常见的结构和我给它们的命名。
注意:
- 有些酸是一样的,比如氮洋酸与氮涪酸其实是同一种物质的两种共存的动态平衡结构,再比如氮酸虽与氮洋酸不同,但它们的酸根部分是一样的,因此只有氮酸盐,而无氮洋酸盐和氮涪酸盐;
- 图中最后一个含氚(T)的物质我不把它归类为酸,而是看作基团汌(<-O<-T)取代磻酸中的羒酸基团得到的酰。
- 这些东西的酸碱性与稳定性都是猜测,很可能“真实”情况完全不是这样,详见后面计算化学小节。
碱类物质也更丰富。水与氧氠等物质可以丢掉不同的氢离子(H+、D2+)形成各种类氢氧根离子(OH3-、OD2-、FnH2-、FnD-、FdH-等),根据电离的难易程度它们的碱性也各不相同。此外还有一些电负性小的有孤电子轨的分子可以接受氢离子也显碱性,例如氨与氠可接受氘离子变成铵根离子(ND42+)和钟根离子(ED52+)。活泼金属氢化物方面,除了对应三种氢化物外,还有一些氕气失去氕正离子后的基团形成的“叠氕化物”(H3-、H22-),没准可充当四维人的“储氕”材料……这些物质的“实际”酸碱度情况很复杂,还跟溶剂有关,即取决于四维世界中的“水”的种类。
某种四维海洋生物圈设定
网友宁宁提出了一套海洋生物圈设定:四维星球的海洋的主要成分并不是单一的水(D2O),而是好几种“类水”的混合。由于“类水”都是极性分子,它们能够互溶,我初步通过估计构成分子的原子量来估计密度,发现这些类水的密度相差不大,不足以让各组分浓度随水深的变化而明显变化,最先我们还假设可能有各种“基”的生物习惯各自生活在各自的水层中维持正常生理活动,尽管它们中的某些也能同时在不同层中生活……注意只有相近的元素的液态极性氢化物才能同时作为四维星球海洋的组成成分,电负性差别太大的元素氢化物之间的酸碱性差别太大,会中和反应生成盐,即大电负性的喜欢电离出氢,小电负性的喜欢用孤电子与氢离子去配位,类似我们的氨气与氟化氢反应生成氟化铵。另外虽然H4O是气体(有效氢键太少导致),但可以假设它在海洋中的溶解度很大,也广泛存在于海洋中,而那些弱极性和非极性分子则难溶于海洋中,逃逸到大气中去了,因此可能的海洋成分主要为氛氨、氛水、氧氨、水、氚水、氤氠、氤氨、氤水的混合物。这些物间最大的差异就是其酸碱度了,虽然涉及多种溶剂准确定义pH值有点难。但有效氢键不同会让这些物质的溶沸点和蒸发速率不同,降雨与向风导致不同陆地上的水资源各成分的含量也有较大差异,没准四维世界的天气预报还会播报近期雨水成分比例……
有机物
我们的三维世界中,有机物专指碳元素形成的复杂化合物。碳的最外层电子数刚好是稀有气体原子的一半,能成最多的键,因此四维空间中外层有10个电子的14号元素是最像碳的了,我干脆就命名成了碳。根据电子数翻倍法则,四维世界的二电子自旋设定下甲烷是CH5,对应到4电子自旋设定就是把各自的电子数翻倍,变成CD5。因此氘(D)是最常见的元素了。这里顺便提一下键线式规则:省略碳原子和氘原子,然后择机省略氕或氚:从键线式出发按照优先补充最多的氘然后是氕最后是氚。比如下面的分子我命名为1-泾-5-氚戊烷:首先不用管氘原子,把端头的泾基(-H2)标出,然后再标记后面的氚原子。碳缺10个电子,氚(T)提供3个后,每个氘(D)贡献两个电子,三个氘最多能填6个,还差一个则默认用氕(H)填,因此不需要再单独标出氕元素。这时直接标氕也是可以的:标出氕后,碳缺10个电子,氕贡献一个电子,相邻的碳贡献2个电子,这时还剩下三个轨道最多需要三个氢原子提供7个电子,容易验证补2个氘和一个氚就是所有补氢方案中氘原子最多的方案了。不过我建议优先画出氚,且命名时也如此。
注:四维世界中其它元素也可以替代碳作为有机物的骨架,比如𥓬苯、乙氮烷等。三维世界的有机物骨架为什么不能是其它元素呢?那是因为氧、氟能够成的键少,无法形成复杂的结构,而氮一般有个孤电子对,相邻的孤电子对的排斥让N-N键不稳定。硼则是缺电子的分子,只能通过更多硼原子共用一堆成键电子来凑数,形成的稳定化合物比较有限。到了四维空间有了氢(H)与氚(T)就很容易突破这些限制,让更多的元素都有五个成键轨道,具体例子可以在四维分子浏览器中找到。
芳香烃
上一篇文章就说过,按不饱和程度(或杂化类型)分,有烷烃烜烃烯烃炔烃四类脂肪烃。甲烷是sp4四维正五胞体立体结构,由于双键的$\pi$电子云,乙烜的所有原子都限制在了垂直于未参与杂化的$p$轨道的平胞内,乙烯有两对未杂化的互相垂直的$p$轨道,所有原子被限制在垂直于它们的平面中,跟三维的乙烯一样是平面分子。苯的类比有sp3与sp2杂化两种。其中sp3杂化的是空间六边形,即C6D12(我命名为萱),而sp2杂化则是平面六边形,即C6D6(我命名为苯)。

注:判断芳香性的休克尔$4n+2$电子规则(来源于分子轨道理论)类比到四维变成$8n+4$电子规则,可验证萱满足该规则,而四维苯有两组垂直的$p$轨道,它们各自形成的离域大$\pi$键互不干扰,各自满足休克尔规则,具有很稳定的二重芳香性。
空间异构
有机物结构非常丰富,通常需要考虑空间异构,下面我们看看手性异构与顺反异构等如何类比到四维。
手性异构与糖类
四维分子照样有手性异构,其旋光性与三维类似。连有五个不同基团的原子为手性原子。值得关注的是三维的葡萄糖与半乳糖本来只有两个手性碳上的差别,类比到四维后碳从四价变成了五价,不管是接氘还是氘氧基,都会让碳上有两个相同的基团而失去手性,即四维世界中的葡萄糖和半乳糖、蔗糖和乳糖不再有区别,也没有旋光性了。题外话:如果避开一个碳上接两个羟基的不稳定情况,不含羰基的糖类很难再跟碳水化合物(CmD2nOn)等价,我只找到一种二乙糖(C4O6D12)是碳水化合物。
双键顺反异构
双键两端的原子各连三个基团,每一边四个原子确定一个三维空间(胞),由于垂直于该胞的pi轨道的出现,两边一定都是共胞的,这将导致一种混合了三维手性异构和顺反异构的新异构现象:双键可以在垂直于pi轨道的空间中旋转,然而无法各自独立地在四维空间中翻转,因此它们要么同手性要么异手性。
三键顺反异构
三键两端的情况就简单了,跟三维空间中普通的顺反异构一样,有两种异构。
累积双键三键异构
四维分子还有累积双键三键:中心原子sp杂化,以直线连接相邻原子,这是三维累积双键的直接类比。设直线方向为x轴、双键端四个原子在空间xyz内,双键的未杂化p轨道在w方向上,则三键两个未杂化的p轨道就只能在剩下的y、z方向上,三键端三个原子就限定在了平面xw内。这个图形也有异构:如果两边原子都不一样,试想我们试图通过旋转交换三键端上的另外两个原子,就必须在包含w轴且不包含x轴的平面内旋转分子,这样势必会把xyz空间中的一个坐标轴反向,即同时改变了双键端的顺序,因此它也有类似双键顺反异构的两种情况。
累积双键异构
四维分子还有种累积双键,它同时具有三维空间中累积双键与普通双键的结构特点,是最复杂的情况了。累积双键中的碳原子采用sp2杂化,因此与它连接的三个原子共面,两对$p$轨道相互垂直,且都垂直于该平面。我们把该平面放在xy平面上,则一个$\pi$键在z方向,一个$\pi$键在w方向,两头的四个原子所在的三维空间分别为xyz和xyw。中间的累积双键碳原子上还单键连接了一个其它原子(或孤电子轨道),但这个原子周围是平面结构,四维空间中能随意翻转,不满足手性条件。因此还是跟普通双键那样只有一组顺反异构,我们可以这样定义两种类型的分子:首先选择一个端头碳A,依次标记为A、B、C,给定连接原子基团的顺序后,我们可以按顺序做三个向量的外积,得到端头碳与三个原子构成的胞的法向量。将碳A与碳C上基团所在胞的法向量m与n做外积张成2-向量m$\wedge$n,该向量理论上跟AB$\wedge$BC(即三个碳所在平面)绝对垂直,因此它们的内积为0,可通过外积的符号来区分两个手性。
四维晶系
三维空间的所有晶体结构可分为7种晶系(三斜、单斜、正交、四方、立方、三方、六方),14种布拉维晶格。四维空间的所有晶体结构可分为23种晶系,64种布拉维晶格,其中10种还有手性。英文维基百科Crystal System词条和《4D对称化学》中都列出了具体的23中晶系,《4D对称化学》给出了晶体参数表详见这个pdf。
下面是我对23种晶系的分析并附上晶轴坐标表达式:六斜晶系:最一般的、完全没有特殊的对称性的平行八胞体。所有的晶面都是斜面,晶轴都是斜轴,晶轴之间的夹角都不是90°,晶面之间的夹角也不是90°。选择合适的坐标系后,四个列向量可组成最一般的上三角阵:$$\begin{pmatrix}a&b&d&g \\ 0 &c&e&h\\ 0 &0&f&i \\ 0 &0&0&j\end{pmatrix}$$
三斜晶系:底胞是长方体的斜柱体,其母线方向与底胞三条边之间的夹角都不是90°。$$\begin{pmatrix}a&0&0&d \\ 0 &b&0&e\\ 0 &0&c&f \\ 0 &0&0&g\end{pmatrix}$$
二斜晶系:一种斜柱柱体。底胞是斜长方形柱,其倾斜方向平行于长方形的一条边,整个四维柱体的母线倾斜方向平行于长方形的另一条边,即两条母线各往两个垂直的方向倾斜。也可以看作是任意两个没特殊对称性的二维格子的直和。$$\begin{pmatrix}a&0&c&0 \\ 0 &b&0&e\\ 0 &0&d&0 \\ 0 &0&0&f\end{pmatrix}$$
单斜晶系:底胞是长方体的斜柱体,其母线方向与底胞三条边之间的夹角只有一个不是90°,即只往那个方向倾斜。$$\begin{pmatrix}a&0&0&d \\ 0 &b&0&0\\ 0 &0&c&0 \\ 0&0&0&e\end{pmatrix}$$
正交晶系:超长方体,所有轴之间都是直角,但轴长不等。$$\begin{pmatrix}a&0&0&0 \\ 0 &b&0&0\\ 0 &0&c&0 \\ 0&0&0&d\end{pmatrix}$$
四方单斜晶系:底胞是正方形柱的斜柱体,其母线方向与底胞三条边之间的夹角只有一个不是90°,只往正方形柱的高方向倾斜,可看作正方形格子与任意没特殊对称性的二维格子的直和。$$\begin{pmatrix}a&0&0&c \\ 0 &b&0&0\\ 0 &0&b&0 \\ 0&0&0&d\end{pmatrix}$$
六方单斜晶系:底胞是正六边形柱的斜柱体,其母线方向与底胞三条边之间的夹角只有一个不是90°,只往六边形柱的高方向倾斜,可看作正三角形格子与任意没特殊对称性的二维格子的直和。$$\begin{pmatrix}a&0&0&c \\ 0 &b&-{b\over2}&0\\ 0 &0&{\sqrt{3}b\over2}&0 \\ 0&0&0&d\end{pmatrix}$$
双四方双斜晶系:两个大小不相同的正方形,其所在的平面为等角关系,有左右手两种。$$\begin{pmatrix}a&0&b&-c \\ 0 &a&c&b\\ 0 &0&d&0 \\ 0&0&0&d\end{pmatrix}$$
双六方双斜晶系:两个大小不相同的正六边形,其所在的平面为等角关系,有左右手两种。$$\begin{pmatrix}a\cos(\theta)&a{\sqrt{3}\sin(\theta)-\cos(\theta)\over 2}&b\cos(\phi)&-b{\cos(\phi) \over 2}\\ -a\sin(\theta) &a{\sqrt{3}\cos(\theta)+\sin(\theta)\over 2}&0&b{\sqrt{3}\cos(\phi) \over 2}\\ 0 &0&b\sin(\phi)&-b{\sin(\phi) \over 2} \\ 0&0&0&b{\sqrt{3}\sin(\phi) \over 2}\end{pmatrix}$$
四方正交晶系:有两条棱相等的超长方体。$$\begin{pmatrix}a&0&0&0 \\ 0 &a&0&0\\ 0 &0&b&0 \\ 0&0&0&c\end{pmatrix}$$
六方正交晶系:底胞是正六边形柱的正柱体,两条高长度不相等,为正六边形与长方形的直积。$$\begin{pmatrix}a&-{a\over 2}&0&0 \\ 0 &{\sqrt{3}a\over 2}&0&0\\ 0 &0&b&0 \\ 0&0&0&c\end{pmatrix}$$
双四方单斜晶系:两个大小不相同的正方形,其所在的平面为等角关系,有左右手两种,且这两组格子的基向量在对方平面内的投影是与对方的格子基向量对齐的。$$\begin{pmatrix}a&0&b&0 \\ 0 &a&0&b\\ 0 &0&c&0 \\ 0&0&0&c\end{pmatrix}$$
双六方单斜晶系:两个大小不相同的正六边形,其所在的平面为等角关系,有左右手两种,且这两组格子的基向量在对方平面内的投影是与对方的格子基向量对齐的。$$\begin{pmatrix}a&-{a\over 2}&b\cos(\phi)&-b{\cos(\phi) \over 2}\\ 0 &{\sqrt{3}a\over 2}&0&b{\sqrt{3}\cos(\phi) \over 2}\\ 0 &0&b\sin(\phi)&-b{\sin(\phi) \over 2} \\ 0&0&0&b{\sqrt{3}\sin(\phi) \over 2}\end{pmatrix}$$
双四方正交晶系:有两对分别等长的棱的超长方体,为两个大小不相同的正方形的直积。$$\begin{pmatrix}a&0&0&0 \\ 0 &a&0&0\\ 0 &0&b&0 \\ 0&0&0&b\end{pmatrix}$$
六方四方晶系:底胞是正六边形柱的正柱体,两条高长度相等,为正六边形与正方形的直积。$$\begin{pmatrix}a&-{a\over 2}&0&0 \\ 0 &{\sqrt{3}a\over 2}&0&0\\ 0 &0&b&0 \\ 0&0&0&b\end{pmatrix}$$
双六方正交晶系:两个不等大正六边形的直积形,相当于双六方单\双斜晶系两平面绝对垂直的情况。$$\begin{pmatrix}a&-{a\over 2}&0&0 \\ 0 &{\sqrt{3}a\over 2}&0&0\\ 0 &0&b&-{b\over 2} \\ 0&0&0 &{\sqrt{3}b\over 2}\end{pmatrix}$$
立方正交晶系:底胞是正方体的超长方体,所有轴之间都是直角,只有一条棱与其它三边长度不相等。$$\begin{pmatrix}a&0&0&0 \\ 0 &a&0&0\\ 0 &0&a&0 \\ 0&0&0&b\end{pmatrix}$$
八方晶系:两个等大正方形,其所在的平面间夹角有可调整的夹角参数,极限情况分别为超立方晶系和共面的两个等大且相差45度的二维四方晶系,两个平面从绝对垂直过渡到共面全平行。非极限状态下两平面之间有手性,是双四方双斜参数中$b=c$且所有轴长度相等的特殊情况。$$\begin{pmatrix}\sqrt{2b^2+a^2}&0&b&-b \\ 0 &\sqrt{2b^2+a^2}&b&b\\ 0 &0&a&0 \\ 0&0&0&a\end{pmatrix}$$
十方晶系:将高度对称的二十方晶系沿着某一条轴伸缩得到,类似立方正交与超立方的关系。 $$\begin{pmatrix}k a&a&a&a \\ a&k a&a&a\\a&a&k a&a\\ a&a&a&k a\end{pmatrix}$$
十二方晶系:两个等大正六边形,其所在的平面间夹角有一个介于90度与60度之间可调整的夹角参数,极限情况分别为六方四方晶系和共胞的三维面心最密堆积,两个平面从绝对垂直过渡到共胞半平行。非极限状态下两平面之间有手性,具体关联的几何意义不明。$$\begin{pmatrix}1&-\frac{1}{2}&e&0\\0&\frac{\sqrt{3}}{2}&\frac{e}{\sqrt{3}}&\frac{2e}{\sqrt{3}}\\0&0&\sqrt{1-\frac{4e^2}{3}}&\frac{-4e^2-3}{2\sqrt{9-12e^2}}\\0&0&0&\sqrt{\frac{16e^4-40e^2+9}{12-16e^2}}\\ \end{pmatrix}$$
双同六方正交晶系:两个等大正六边形的直积形。$$\begin{pmatrix}a&-{a\over 2}&0&0 \\ 0 &{\sqrt{3}a\over 2}&0&0\\ 0 &0&a&-{a\over 2} \\ 0&0&0 &{\sqrt{3}a\over 2}\end{pmatrix}$$
二十方晶系:晶格为由正五胞体体心与其四个顶点张成的平行八胞体。整体具有正五胞体对称性,所有棱长与夹角都相等。该排列中每个原子与周围10个距离相等的原子相邻,这10个原子的排列模式为两个互为对偶的正五胞体的顶点。$$\begin{pmatrix}k a&a&a&a \\ a&k a&a&a\\a&a&k a&a\\ a&a&a&k a\end{pmatrix}$$其中:$k=\sqrt{5}-4$。
超立方晶系:所有棱等长、所有角都是直角的超立方体。$$\begin{pmatrix}a&0&0&0 \\ 0 &a&0&0\\ 0 &0&a&0 \\ 0&0&0&a\end{pmatrix}$$
注:Tesserxel中物质结构>四维晶格中有对称性较好的晶格模型可供查看。
金刚石结构类比
金刚石与石墨都是碳单质的同素异形体。四维碳单质根据杂化类型分成了三种:
- sp2杂化的平面石墨结构,为二维片状结构,每个碳原子都有两个互相垂直未杂化的p轨道形成两个独立的离域大$\pi$键,同样具有导电性,亦可做润滑剂;
- sp3杂化的“金刚墨”结构,为三维金刚石片胞层状结构,每个碳原子都有未杂化的垂直于片胞层的p轨道形成离域大$\pi$键,具有导电性,层间仅有范德华力,可滑动,可做润滑剂;
- sp4杂化的超金刚石结构;
超金刚石是全新的四维结构。我们有必要研究一下其结构。不妨假设每个碳都连接相邻五个碳,键角都是标准sp4杂化正五胞体中的键角,且每个碳原子、每个碳碳键的地位相同。有没有这样的结构呢?三维金刚石是面心立方体结构,三维的金刚烷可以看做取正四面体顶点和棱心作为骨架,然后将棱心原子向外拉,直到顶点和棱心原子间满足sp3键角的要求。这里同时出现了立方体与正四面体,是因为立方体交替取一半的顶点就得到正四面体,而超立方体交替取一半的顶点得到的是正十六胞体,类比失败。四维空间还是可以存在超金刚烷结构的,即取正五胞体各顶点和棱心作为骨架,同样往外拉,然而我们无法保证顶点和棱心同时满足sp4杂化的理想夹角呢?有个不需要复杂计算的简便方法可验证:拉至棱心与顶点的两条线段平行于顶点至正五胞体中心时,根据平行四边形的对角相等可知这些夹角肯定都等于sp4杂化的理想夹角。Tesserxel中绘制出来可发现这个模型满足顶点与棱的对称性。这就说明超金刚石的晶体结构不是超立方晶系家族,而是属于四维二十方晶系家族。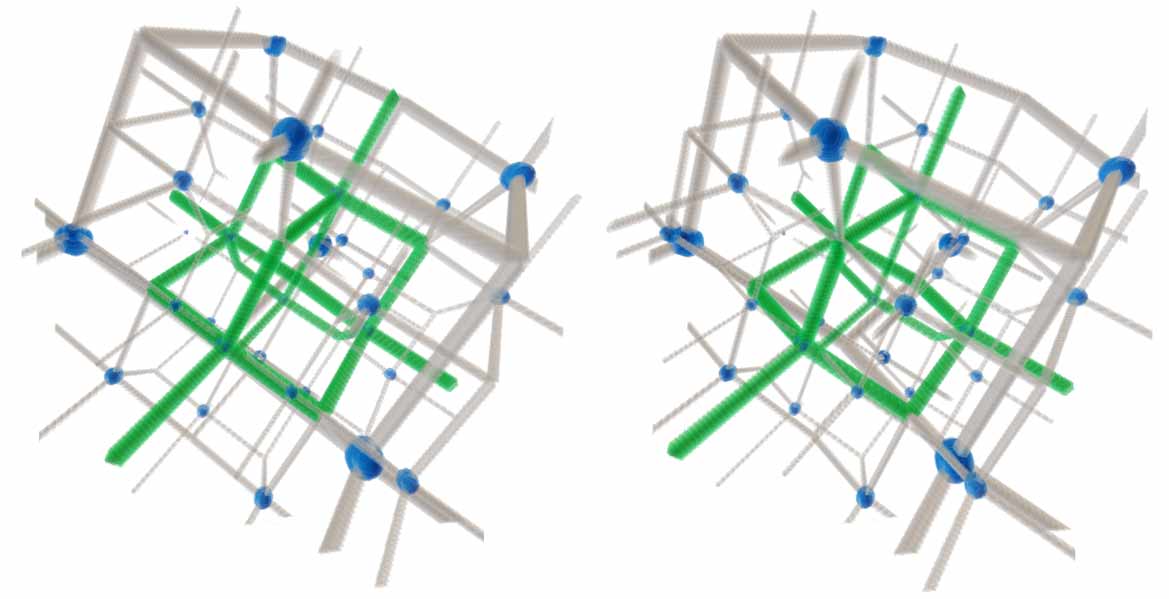 五氧化二磷也有金刚烷的结构,类比到四维或许可以有一种超金刚烷结构的十五氧化五碓。四维五氧化二磷以及更高氧化态的七氧化二磷也存在,它们是类似三维金刚烷结构的十氧化四磷和十四氧化四磷,只是配位氧的数量不同。(碓(G)原子序数:36,价电子排布:3s43p8,硝族,常见化合价为4价;磷(P)原子序数:38,价电子排布:3s43p10,氮族,常见化合价为3价。)
五氧化二磷也有金刚烷的结构,类比到四维或许可以有一种超金刚烷结构的十五氧化五碓。四维五氧化二磷以及更高氧化态的七氧化二磷也存在,它们是类似三维金刚烷结构的十氧化四磷和十四氧化四磷,只是配位氧的数量不同。(碓(G)原子序数:36,价电子排布:3s43p8,硝族,常见化合价为4价;磷(P)原子序数:38,价电子排布:3s43p10,氮族,常见化合价为3价。)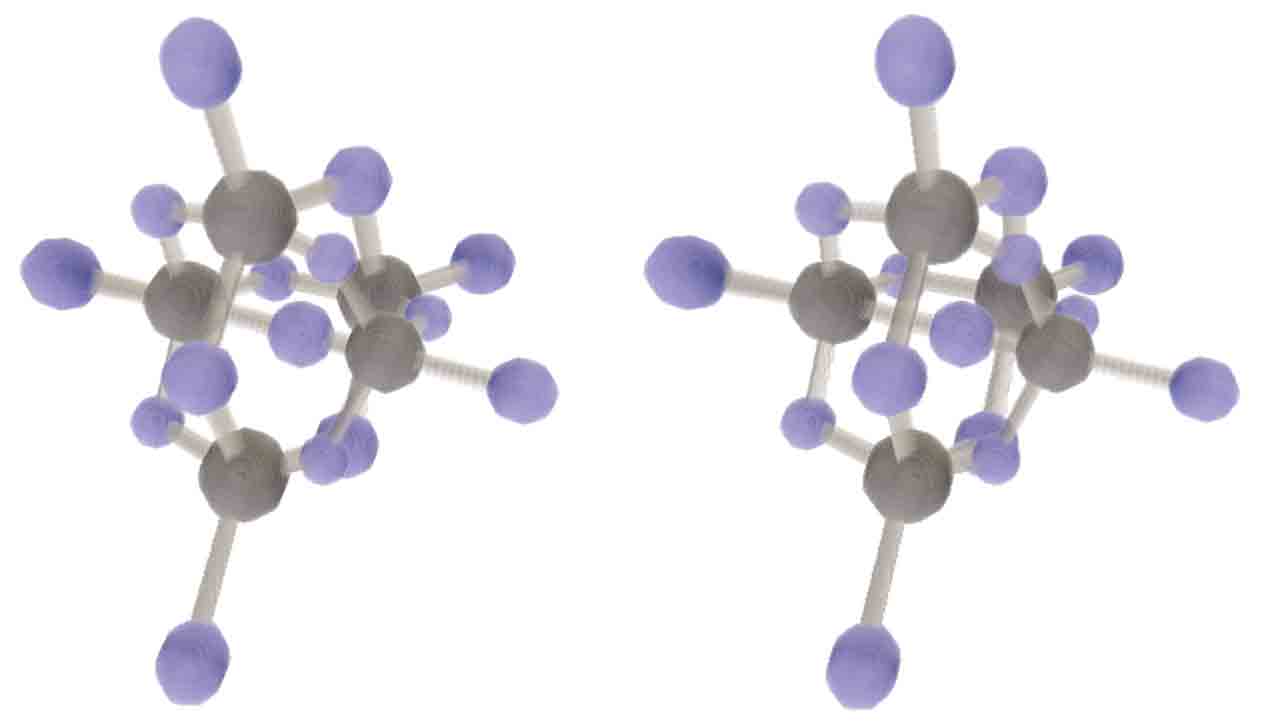
四维分子浏览器
虽然对“真实”的四维化学我们了解甚少,不过出于好玩我还是写了一个假想的四维化学常见物质结构式查看器,并支持与Tesserxel示例库交互生成4D分子模型。(涉及金刚烷的2D结构式显示有bug,请无视)我还自己命名了一些官能团的名称,有些则采纳了《4D对称化学》中取的名称,比如官能团“酢”(-CO2)、某些氨基酸结构的类比等。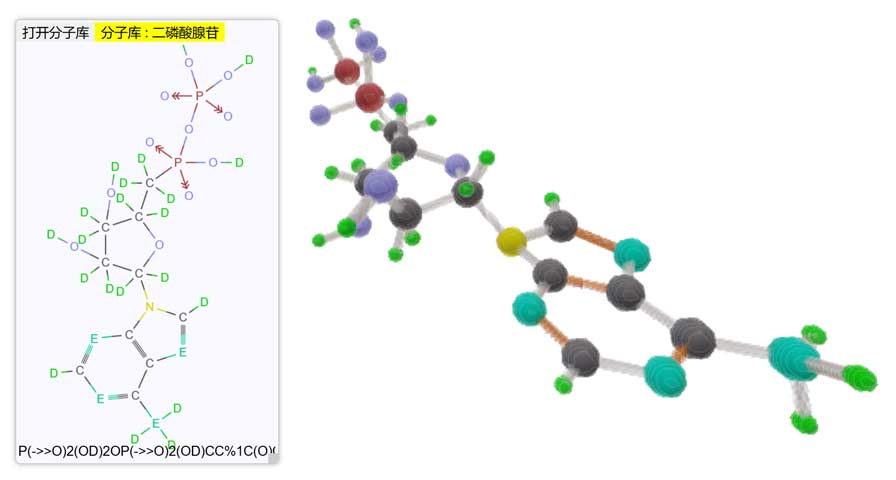
每次刷新可随机摇出分子,或者点“手气不错”来刷出下一个分子。随机生成的分子会存到后面的历史记录中。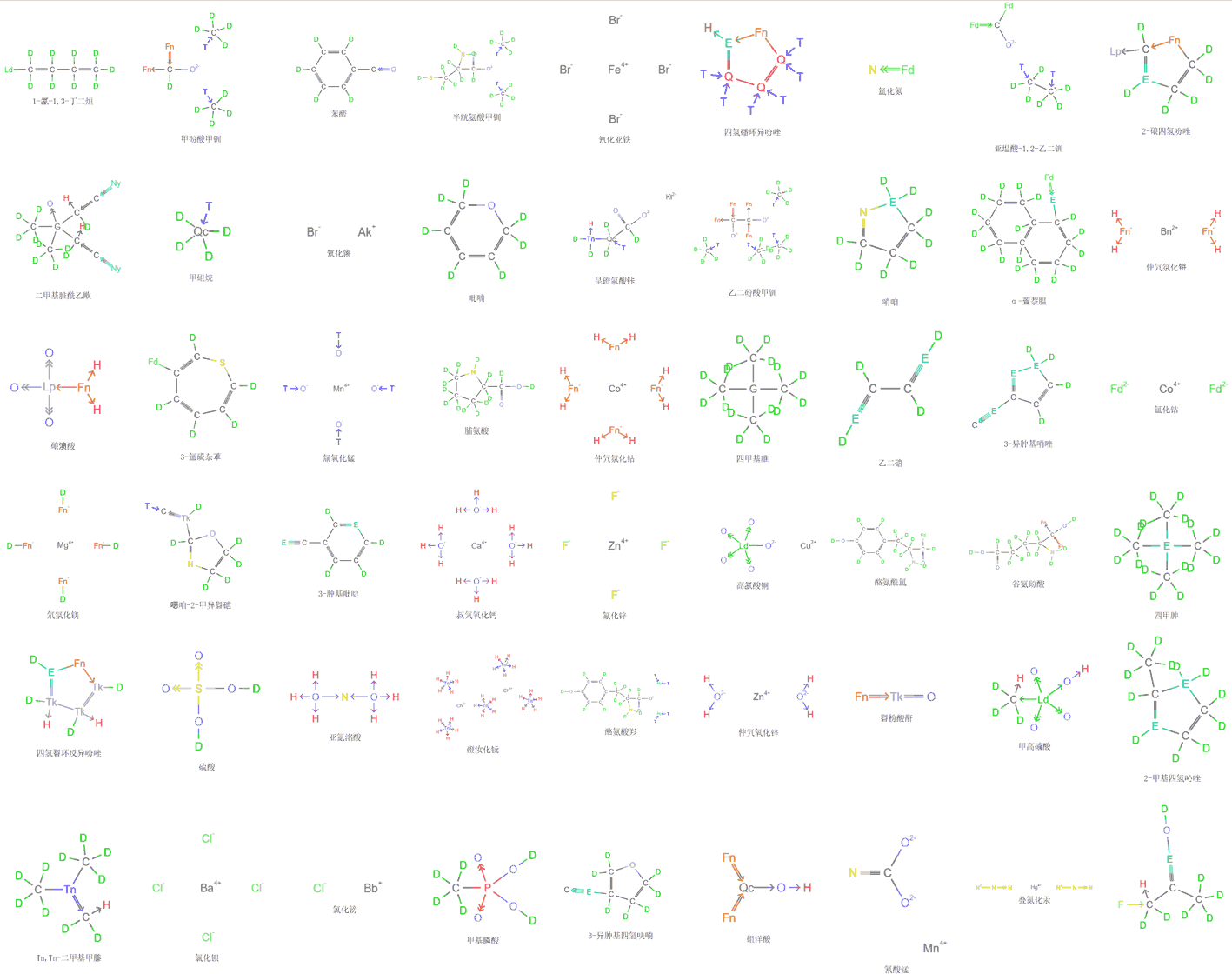
粒子物理
由于要对四维立方反比导致原子不稳定进行修正,会极大影响原子分子的性质,这些简单类比很可能全部失效。搭建四维世界观最理想的方式是直接指定最基础的“上帝”物理法则,然后所有一切都不用再设定,从此出发推出一切物理化学、自然甚至生物学相关的性质。现实世界中这种“上帝”物理法则还没有完全被发现,目前最接近的物理理论就是量子场论与广义相对论。然而引力的量子化还没有解决,量子场论无法与广义相对论互相兼容。弦论是整合两者的可能最终理论,但目前没有实验结果支持它。这篇文章我们先忽略引力,只关注量子场论部分。
量子场论简介
量子力学告诉我们,微观粒子是以概率波的形式存在的。薛定谔方程就是描述的单粒子的位置概率波函数随时间怎样演化的。然而随着研究的深入,人们发现所有粒子都是量子场,描述三维空间中粒子的位置有三个自由度,而要描述一个场就需要给出空间中每个点上场的值,自由度是无穷维的,整个量子场各种不同分布取值都有独立的概率,其概率波函数也变成无穷维的了,因此我们不直接像薛定谔方程那样求解波函数,而是通过一些跟费曼图有关的技巧计算粒子作用所有可能的演化路径贡献的概率幅总和来预测物理实验结果。这就是量子场论的基本数学逻辑。
量子场论认为,整个宇宙空间中都弥散着一些量子场,粒子是场的激发态,类似波函数描述的振动模式。每种基本粒子都对应一个量子场,例如电子场、光子场等。粒子间相互作用本质是场之间的耦合作用:例如,两个电子(电子场)通过交换光子(电磁场的振动)产生排斥力。量子场论跟狭义相对论(不含引力)是兼容的,它是目前实验验证过的最精确的物理理论。
标准模型
到底有哪些基本粒子呢?标准模型给出了所有粒子以及它们之间的相互作用。费米子是有半自旋的粒子,构成物质,如电子、夸克等。标粉色的是6种夸克,标绿色的是6种轻子,轻子的质量比夸克小很多,并因此得名。把它们分成了3列,叫做“世代”,不同世代的对应粒子除了质量不同,其它性质差异不大。从左到右分别为第一、二、三代。我们正常的原子都是由第一代的夸克(上下夸克组成质子、中子)和电子组成的。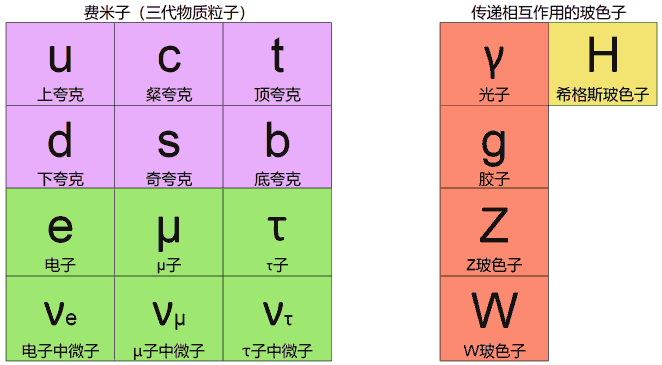
这些粒子如何相互作用呢?电子和夸克带有电荷,与电磁场(光子)有相互作用;夸克与胶子带有“色荷”,通过胶子进行强力作用,将质子中子束缚形成原子核;此外对于左手费米子还有通过W及Z玻色子传递的弱相互作用力,它会引起原子核放射性衰变,而中微子不带电,只参与弱相互作用力与引力作用;最后希格斯玻色子给所有费米子以及W、Z玻色子赋予了质量。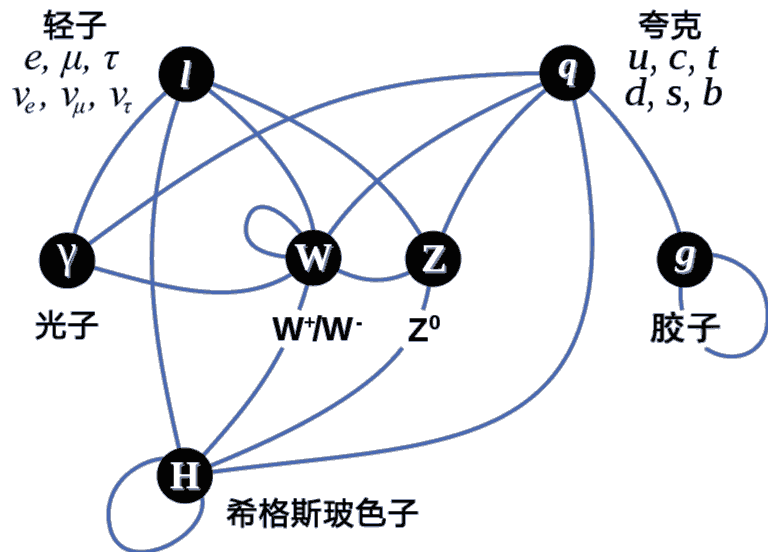
四维场论的标准模型
四维空间的立方反比衰减规律导致若电子只受到原子核的电磁力,则不再有最低离散能态,电子会不断辐射能量最终落入原子核,因此我们需要引入不同于现实世界的物理机制来消除它。四维原子的不稳定性没有标准的规避解决办法,比如这篇文献发现五维及以上氢原子可能有离散能级,但维度不适用于四维;Hadroncfy认为直接沿用三维的模型虽然导致原子不稳定,但没准有稳定的分子轨道,然而我认为希望渺茫,有兴趣的朋友可自行计算探究。
这里首先要介绍的是《对称4D化学》中提出的新标准模型:通过在现有的$\mathrm{SO}(10)$对称性的大统一理论(Grand Unified Theory)之上加入新的费米子三个世代之间的对称性$\mathrm{U}(3)$引入新的相互作用,既交换了 3 代费米子(由 U 玻色子),又在同一代物质(由 V 玻色子)之间产生了轻微的排斥力,这种排斥力可以阻止电子螺旋进入原子核,让原子稳定变得可能。
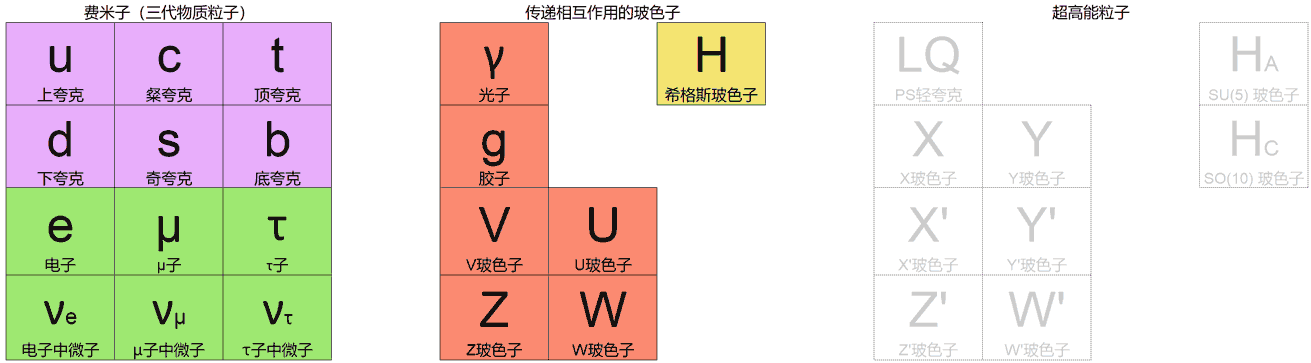
这个模型看起来很棒,但作者也坦言只是图好玩造的,很难说是真的给出了四维世界正确的微观理论。因为标准模型的参数非常多,模型中各种粒子均要通过严格计算才知道是否满足稳定性。目前大家都只是定性地给出粒子模型,而无法确切得知是否彻底解决了四维世界中的所有不稳定、重整化等积分发散问题,从而自下而上构筑一个物理上最“真实”的四维世界。
4DEnthusiast的碱金属性质估计
有趣的是,4DEnthusiast假想的四维化学同样采用的是引入新的带质量的自旋为1的矢量玻色子的方式制造短程斥力来防止电子坠落,不过他并没提出其它的包括交换世代间费米子的超对称模型。
他通过计算发现,四维原子的半径变化会非常剧烈: 三维世界中最小的氢与最大的铯元素半径也最多只相差10倍,四维引入指数衰减的短程力后这个倍数可以到上百倍,体积比可以达到十的8次方,它们几乎不可能以非离子化元素的形式出现。如果以某种方式将单质分离出来,它们可以在室温下形成稳定的等离子体,且这种气体能够还原与其接触的几乎所有物质。在足够低的温度下,它们可能会凝结形成密度极低的比普通固体轻数百万倍的金属。由于任何可见光子都很容易使电子从这种金属中逸出,4DEnthusiast猜测四维碱金属可能呈现深红色甚至黑色。4DEnthusiast并没有说这种类碱金属就是周期表的所有第一列元素,因为他通过角动量的计算发现,很可能从三维类比到四维的主量子数、角量子数所对应的能量差异很大导致元素周期律变得混乱,导致能级交错规律完全消失,我们之前给的所有版本的元素周期表可能都是错误的。目前他还没有给出具体的周期表。
四维核壳模型
4DEnthusiast认为原子核的内部细节大多与化学关系不大,因为它们比普通电子轨道小得多,通常可以视为点状结构。然而核物理学决定了哪些元素存在及相应丰度,因此还是值得考虑。《对称4D化学》中提出了能够估计各种原子是否具有放射性或放射半衰期的核壳模型:像电子轨道那样算出每层需要几个电子才到稀有气体稳定结构,对于原子核同样可计算质子和中子填充满原子核各层级的数目,不过对于原子核还需要结合自旋角动量和轨道角动量的耦合。他们还草拟了一些氦融合、氦捕获和其它几个核反应式,试图解释恒星演化。4DEnthusiast认为引入新的短程力会让电子与核子之间的作用变得非常不同:假设弱反应$p + e^- \rightarrow n + \nu_e$仍然可能发生,且反应前后短程力对应的“s荷”(类似电磁力对应电荷)是守恒的。根据这个反应式,电子带s荷,而中微子不带任何s荷(否则会干扰化学反应),因此中子必须带一些s荷。最简单的想法是让中子和电子带相同的s荷,而质子不带s荷,但这会导致电子主要通过短程力而不是弱力参与相互作用,为避免这种情况,就需要核子的s荷比电子的大得多,中子的s荷比质子的略多,从而保持上面弱反应方程的s荷守恒。由于中子带s荷,质子数相同而中子数不同的核素的化学性质也会存在显著差异,以至于它们可能被视为完全不同的元素,这也意味着质子中子比足够高的核素中,电子可以完全克服s力落入原子核吸收转化为新的核素。虽然有如此大的不同,但4DEnthusiast认为有机物的骨架元素还会是在正常的碳元素附近。
其它周期律世界观设定
《对称4D化学》中给出了另外两种不同的周期律设定:其中第一种为Higher Space论坛中Vector提出的2自旋电子系统,这其实也是4DEnthusiast的设定:假定四维世界只存在一种手性自旋(比如左等角旋转)的电子,正电子的自旋则都是另一种手性。本文的四维设定则是假设两种电子同时存在且几乎比例相等。“真实”的四维世界采用哪种模式完全要靠实验才能确定:想象一下原本有两个只有左手和右手电子的世界,(如果天生就是四自旋态世界,也可以通过手性磁场筛选分离出不同手性电子来强行组成单手性的原子)某一天它们相遇了,两个世界中的元素之间开始疯狂交换各自的电子最终达到两种手性平衡的结构,所有元素在原子序数不变的情况下从两自旋的周期律变成四自旋的周期律。举个例子:本来是填满两个电子的惰性元素氦(两自旋周期律意义下)突然发现原来对方填入自身手性电子的轨道都还是空着的,于是它们各自交换一个电子变成了两个原子序数为2的氘原子(四自旋周期律意义下),然后形成D2分子。注意这个过程原子核、原子序数都没变,因此是一种奇特的化学反应而非核反应。
第二种为忽略轨道角动量必须是简单2-向量的事实,强行认为左右手等角旋转的波动相互独立,可自由组合出一些很奇怪的组合:现在每个电子不仅只用s、p、d单字母表示,而是ss、sp、ps、sd、pp这样的双字母表示,导致元素多得更吓人: 基于这个模型他们也提出了核物理、分子多中心键等设定。然而数学上计算可知出现非简单2-向量的轨道角动量是不自洽的,可直接认定为错误理论,但去想象一下图个乐也不错。
基于这个模型他们也提出了核物理、分子多中心键等设定。然而数学上计算可知出现非简单2-向量的轨道角动量是不自洽的,可直接认定为错误理论,但去想象一下图个乐也不错。
个人认为2自旋电子系统虽然与三维类似,但从几何上想也有点牵强,因为在四维空间中只选择出两个旋转方向而不是四个直接就破坏宇称(手性)了,但至少没违背数学原理,嗯,反正我们世界也宇称不守恒……其实反正四维世界都是假的,也无所谓了。下面是相关链接:
- Alternative Chemistries:4DEnthusiast的四维化学,包含粒子物理设定、四维键能计算、元素性质预测等硬核内容。电子采用手性两自旋态设定。(目前看到的最细致的四维微观物理设定,不过也没解决无法重整化的问题)
- 对称4D化学:与本blog设定相同的四自旋态系统
- Vector’s 4D Chemistry : Higher Space论坛上发布过的手性两自旋态电子设定
- Planet’s 4D Chemistry : 允许非简单轨道角动量的四自旋态系统,对称4D化学的灵感来源
- Quack’s Old 4D Chemistry 对称4D化学的旧系统,也是允许非简单轨道角动量的四自旋态系统





