《四维计算机图形学：渲染篇》说到了如何渲染四维几何体，但还没提到四维几何体的数据从何而来。本文就来探讨总结一下常见的四维几何图形数据生成算法。
特色内容
小复习
作为这篇文章的重点基础知识，我们先来复习一下那篇文章已经介绍过的胞腔复形：除了顶点需要单独描述坐标外，其它高维面我们均描述组成它的边界的序号。比如
- 一个点：
顶点：{()0} - 一条线段:
顶点：{(-1)0,(1)1}
边：{(0,1)0} - 一个正方形:
顶点：{(-1,-1)0,(-1,1)1,(1,1)2,(1,-1)3}
边：{(0,1)0,(1,2)1,(2,3)2,(3,0)3}
面：{(0,1,2,3)0} - 一个四棱锥:
顶点：{(-1,-1,0)0,(-1,1,0)1,(1,1,0)2,(1,-1,0)3,(0,0,1)4}
边：{(0,1)0,(1,2)1,(2,3)2,(3,0)3,(4,0)4,(4,1)5,(4,2)6,(4,3)7}
面：{(0,1,2,3)0,(0,4,5)1,(1,5,6)2,(2,6,7)3,(3,4,7)4}
胞：{(0,1,2,3,4)0} - 一个正方体:
顶点：{(1,1,1)0,(1,1,-1)1,(1,-1,1)2,(1,-1,-1)3,(-1,1,1)4,(-1,1,-1)5,(-1,-1,1)6,(-1,-1,-1)7}
边：{(0,1)0,(1,3)1,(2,3)2,(0,2)3, (4,5)4,(5,7)5,(6,7)6,(4,6)7, (0,4)8,(1,5)9,(2,6)10,(3,7)11}
面：{(0,4,8,9)0,(1,5,9,11)1,(2,6,10,11)2,(3,7,8,10)3,(0,1,2,3)4,(4,5,6,7)5}
胞：{(0,1,2,3,4,5)0} - 对于四维图形也一样，只是胞不再只有单条数据，比如一个正五胞体:
顶点：{$(1/\sqrt{10},1/\sqrt{6},1/\sqrt{3},1)$0,$(1/\sqrt{10},1/\sqrt{6},1/\sqrt{3},-1)$1,$(1/\sqrt{10},1/\sqrt{6},-2/\sqrt{3},0)$2,$(1/\sqrt{10},-\sqrt{3/2},0,0)$3,$(-2\sqrt{2/5},0,0,0)$4}
边：{(0,1)0,(0,2)1,(0,3)2,(0,4)3,(1,2)4,(1,3)5,(1,4)6,(2,3)7, (2,4)8,(3,4)9}
面：{(0,1,4)0,(0,2,5)1,(1,2,7)2,(4,5,7)3,(0,3,6)4,(1,3,8)5,(4,6,8)6,(5,6,9)7,(2,3,9)8,(7,8,9)9}
胞：{(0,1,2,3)0,(0,4,5,6)1,(1,4,7,8)2,(2,5,8,9)3,(3,6,7,9)4}
注意正五胞体本身也是个四维胞腔，按理说可以继续引入下一层的胞腔列表，但对于四维几何体渲染来说知道三维胞腔就够了，四维胞腔结构一般用不到，因此上面没再写四维胞腔了。
四维几何体的常见生成算法
简单的图形是可以手写出来的，复杂图形就必须靠生成了，常见的生成算法有柱化锥化直积等等，其实很多三维的算法推广到四维也能用，比如凸包算法、隐函数曲面建模算法、网格细分算法、布尔运算等等，这些话题要仔细不漏地说完可能得写成像砖一样厚的书，我们也没有精力一一去实现它们，这里就只讲一些简单实用的生成算法，下面先从最简单的锥化说起。
$x$的锥化的边界$\partial \widehat{x}=x+\widehat{\partial x}$$=x+\widehat{a+b}=x+\widehat{a}+\widehat{b}$
锥化
对于一个平直的胞腔复形C，我们在它所在超平面外找一点作为锥点即可进行锥化操作。锥化可递归地描述：给定点P，n维胞腔的锥化就是与新顶点构成n+1维的新胞，而这个新胞的边界由原n维胞和所有该胞的n-1维边界的锥化构成，由于点没有边界，它的锥化特殊些:是一条以该点与点P为端点的线段。一般的编程算法则更接近从下往上的描述：给定点P，将它加入胞腔复形中的顶点列表；然后，将它与原复形中的所有顶点相连成新的边，加入胞腔复形中的边列表；然后，将原复形中的所有边，以及上一步中每个边的端点与点P相连产生的新边共三条边构成新的三角形面，加入胞腔复形中的面列表；然后，将原复形中的所有面，以及上一步中每个面的边界与点P相连产生的新面构成新的胞，加入胞腔复形中的胞列表……
柱化
不同于锥化将每个图元都与定点相连，柱化则是将整个复形平移复制一份，然后将复制前后的图元两两相连，构成柱体。对于一个平直的胞腔复形C，给定一个不平行于它所在超平面的向量即可进行柱化操作：给定向量V，首先将胞腔复形整个复制一份并沿该向量完成平移，这个过程中顶点与各n维胞腔均复制成了两份，这两份即柱体的“顶面”和“底面”，下面生成侧面：n维胞腔对应的侧面由这些边界组成：一是在底面的该n维胞腔，二是顶面复制出来的对应胞腔，三是该n维胞腔的边界对应的侧面。同理，由于点没有边界，故点的侧面就是以底面上该点与顶面该点为端点的线段。
两图形的直积将会把所有组成它们的子复形像乘法分配率展开那样两两直积
上图例举了一些项
直积
因为不存在很直观的三维类比，直积的理解没有柱化和锥化容易。直积在代数上更容易理解：它就是一种乘法。比如它满足乘法分配率、交换律、结合律等，且n维图形与m维图形的直积得到一个n+m维图形。我在《玩Tesserxel（二）：场景交互介绍》的几何体>直积形系列场景小节里提到过，直积形$A \times B$有两个边界，一是$A$的边界与$B$的直积，二是$B$的边界与$A$的直积，写成公式即为：$$\partial(A\times B)=\partial A \times B + A \times \partial B$$通过这个公式，我们就能够从低维到高维自下而上地构造直积形了。以两个二维图形的直积为例，首先我们将图形A复制图形B顶点数量那么多份，其中复制出的每份图形顶点的$x$、$y$坐标不变，$z$、$w$坐标则设为图形B顶点的$x$、$y$坐标，现在得到了直积形的所有顶点坐标。刚才我们将图形A沿图形B的所有顶点复制了一份，其实相当于完成了图形A的所有$n$维胞腔与图形B的$m=0$维胞腔的直积，因此我们跳至从$m=1$开始，按维数从小到大的顺序，对每个图形A中的$n$维胞腔与每个图形B中的$m$维胞腔，按上面的公式构造$n+m$维胞腔：首先$m=1$即把A图形的各维度所有胞腔都沿着B图形的所有边柱化，然后接下来$m=2$即把A图形的各维度所有胞腔都与B中的所有二维面直积……注意，将$n+m$维胞腔加入胞腔列表时还需要单独维护一张直积索引表，其键为原n维胞腔和m维胞腔的序号，值为这块$n+m$胞腔的编号，因为后面要用于构造高维胞腔的直积的边界，到时才方便快速查找到它的编号。
旋转体与参数化曲面
旋转体在拓扑上可以看作截面与圆周的直积。比如三维空间中的圆环（轮胎）面拓扑等价于两个圆周的直积，虽然按理说得到的是四维图形双圆柱，但在不破坏顶点连接关系的情况下重新改变顶点坐标就可以得到三维空间中的普通圆环（轮胎）面，这启发我们很多数学图形都可以先通过直积网格来间接生成。
数学上最常见的描述曲面的方法就是参数方程了，即给定两个有各自独立取值范围的变量$u$与$v$，通过向量值函数$\mathbf{f}(u,v)$来描述它，直观上它就是把通过坐标$u$、$v$描述的一块平面矩形映射到三维空间，包裹成一张曲面。四维参数化曲胞也同理，只是将参数变成了$u$、$v$、$w$三个，通过向量值函数$\mathbf{f}(u,v,w)$把通过坐标$u$、$v$、$w$描述的一块长方体映射到四维空间，包裹成一张曲胞。
生成参数化曲面的胞腔其实跟数学的描述一样:首先生成一个长方体网格，然后通过映射函数改变相应顶点坐标即可。长方体网格可以通过三条分段了的线段的直积来生成。
参数化曲胞几乎可以描述之前四维空间系列中描述的常见曲胞，比如球环环球圆环环双圆环等等。这些曲胞的参数方程可以自己推导，也可以去higerspace网站中的wiki上查到。
值得注意的是，球面/超球面虽然是旋转体，也很容易写出参数方程，但在拓扑上并不是直积形，因为南极和北极位于旋转轴上，如果按直积或参数方程的算法，它们也将会有旋转轨迹，产生一系列多余重复的多余点、边等结构。一般情况下重复点并不影响渲染，只是会多占用一些内存资源，如果你实在不能忍受，则可采用特殊方法生成球面/超球面，单独处理极点附近，或采用顶点合并算法来剔除多余的图元。（p.s. 通用的顶点合并算法很复杂，要考虑的情况很多，比如一个三角形的两顶点被合并，除了删除顶点和两点之间的边外，三角形面也将不复存在，并退化成一条边）。
最后要提醒的一点是，通过参数方程生成的立方体网格中的六面体的8个顶点可能会存在不共胞的情况，会导致模型渲染时出现一些问题，解决它们有点复杂，具体我们会在后面讨论。一般比较规则的数学图形例如双圆环、圆环环、球环、环球等都不会遇到该问题。
四维隐函数方程曲面
四维隐函数方程曲面$f(x,y,z,w)=0$的建模其实跟渲染篇中的求截面非常类似：把$u=f(x,y,z,w)$当成是五维空间中的曲面方程，它可以通过直积生成四维立方体网格后，再把所有顶点的第五维坐标$u$按公式$u=f(x,y,z,w)$得到。得到五维曲面的胞腔复形后，使用截面算法便可截取出$f(x,y,z,w)=0$的截面了。
正多胞体及其衍生物生成
我们知道三维正多面体有5种、四维正多胞体有6种。之前我们都是像参观博物馆似地看它们，数学家们是怎么发现并构造它们的呢？正多胞体、以及相应各种截角（截半、截棱、各种大小斜方全截等等）版本的正多胞体的结构是高度对称的，反射与群论相关数学工具可以得到所有的东西：这些高度对称的东西都可以通过像万花筒一样的方式不断镜像反射生成出来（叫做Wythoff构造），具体细节网上已经有写得很精彩的文章了，请参阅下面的链接：
- 赵亮(Pywonderland)的文章《Todd-Coxeter 算法和 3D/4D 均匀多胞体》 介绍了如何摆放“镜子”、找到反射的顶点初始位置，以及如何通过群论中的陪集枚举算法计算反射出的顶点。
- Mikael Hvidtfeldt Christensen 的文章《Building 4D polytopes》 其中有在线交互式的3D模型演示，让你清晰直观地看见正多面体是怎样生成的。
我想补充两点：
1.两篇文章都提到了最重要的陪集枚举（Todd-Coxeter）算法并做了一些解释与演示，但要写出一个真正能够用的程序需要处理的细节非常多，要想自己尝试写程序的读者请参考《Handbook of Computational Group Theory》这本书中的相关章节，其中有非常详细的伪代码描述算法。
2.按照以上两篇文章通过陪集枚举算法生成了顶点列表、边列表、面等列表之后，并没有说怎样得到胞腔复形数据结构中所需要的n-1维胞组成n维胞的关系。其生成方法不复杂，我们以找顶点与边的连接方式为例：首先生成整个反射群的群表（即枚举平凡子群{e}的陪集），由于每个“基本区域”与反射群的群元素一一对应，因此它也是一张所有基本区域的反射表，即表中以数字编号的方式记录了任一区域$i$通过反射$k$到达的新区域$j$。接下来我们分别生成顶点与边的陪集列表。这些列表其实记录了每面镜子将把哪个顶点/边反射到哪个另外的顶点/边上。顶点、边的中心都位于基本区域的边界上，它们被多个基本区域所共用，而共用了同一个基本区域的顶点与边其实就是相连的，因此如果我们能够获得每个基本区域上的顶点/边/面的编号，就可以解决这些点线面之间连接关系的问题。比如下图中我们发现，边a同时被基本区域0~3公用，这四个区域中的所有顶点(P与Q)就构成了它的端点。其实这个方法不止能生成n-1维至n维胞腔的连接关系，它也可以帮我们快速找到一个顶点属于哪些面、一个胞中的所有棱等一切这样的连接关系。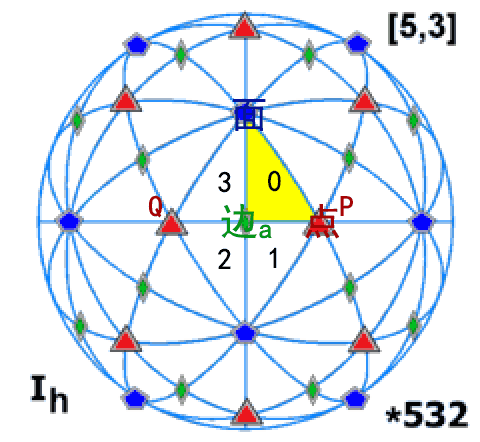
现在还有一个问题没解决：如何知道每个基本区域上的顶点/边等的编号呢？首先所有的0号图元都是单位元，即不做任何反射的那个初始基本区域中的顶点/边。其它基本区域与它的顶点/边一定都是通过一系列的反射生成的。我们只需要将生成每块基本区域的所有反射步骤作用到顶点上，就能知道新的基本区域对应的顶点编号了，不断查顶点的陪集表就可以完成这件事。
最后再说下生成每块基本区域的所有反射步骤的细节。我们逐步建立这样一张表，其键是基本区域的编号，值是反射步骤序列。首先，0号区域不需要任何反射，直接写入空序列即可；然后我们逐行扫描陪集表通过反射得到新区域。如果查询到新区域已经生成了反射序列，则跳过；若没有，则在目前区域的反射步骤上加上刚做过的反射即得到新区域的反射步骤。
截角正多胞体生成方法
正多面体还比较简单，截角、过截角、截棱等多面体如何生成呢？这些多面体的Wythoff构造中，初始顶点位置不再位于基本区域的一角，有些是在边上，有些则是位于基本区域内部，而且多面体的边、面、胞等可能不止一种形状，它们的对称性也不一样，需要分别生成各自对称子群对应的陪集表，最后还是以相同的方法通过基本区域来找连接关系，但由于同维度图元的种类不止一种，通过陪集枚举列举它们都是各自从0开始编的号，将它们先后添加至胞腔列表后，对于后续高维胞腔需要索引它们做边界时，就要注意给后添加的那一批图元统一增加一个偏移值。下面我们举一些例子：
截角正多面体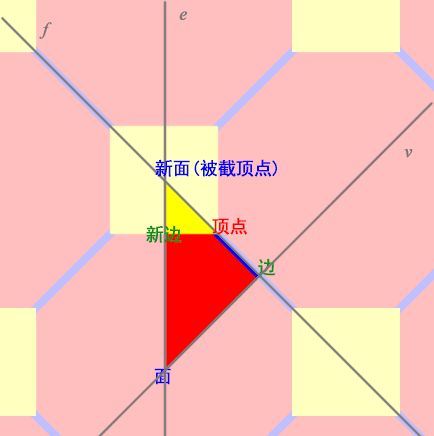
比如对于三维的正多面体（或二维正多边形镶嵌亦适用）顶点被截形成的截角正多面体，我们应该生成以下图元的对称子群生成元的陪集列表：
| 代号 | 图元 | 对称子群生成元 |
|---|---|---|
| Ft | 新面表（原顶点位置） | $f,e$ |
| E | 原边表 | $f,v$ |
| F | 原面表 | $e,v$ |
| V | 新顶点表 | $f$ |
| Et | 新边表 | $e$ |
我们发现，截角多面体比正多面体多了一些图元，它们的中心在基本三角形的边上而不在顶点上，这些图元的对称性要少一些，陪集枚举生成的数量也要多一些。生成了陪集后，我们就能通过寻找正多面体图元间连接关系的算法找出下面的图元构成关系：（其中A->B表示记录每个图元B由哪些A构成的表）
- V->E、V->Et
- Et->Ft、E->F、Et->F
得到这些连接关系后，我们就能构造相应胞腔复形的边表与面表了：边表就是把表V->E与表V->Et合并，面表则麻烦一些：由于储存的是索引值，边表中所有的新边都排在原边后，即陪集表中的0号新边在边表中的序号其实等于原边数，需要将面表中出现的所有新边序号加上该偏移值，原面由两种边构成，一种是原边，另一种是截出来的新边，需要将表E->F与Et->F合并。
大斜方截半正多面体
大斜方截半正多面体的特点是它的顶点完全位于基本三角形内部，对称性最少，生成出的多面体是最复杂的。我们同样画出各图元在基本三角形中的位置，然后列出它们的连接关系表：
| 代号 | 图元 | 对称子群生成元 |
|---|---|---|
| F | 原面 | $v,e$ |
| Fe | 边截面 | $f,v$ |
| Fv | 顶点截面 | $e,v$ |
| E1 | 边1 | $e$ |
| E2 | 边2 | $v$ |
| E3 | 边3 | $f$ |
| V | 顶点 | 无 |
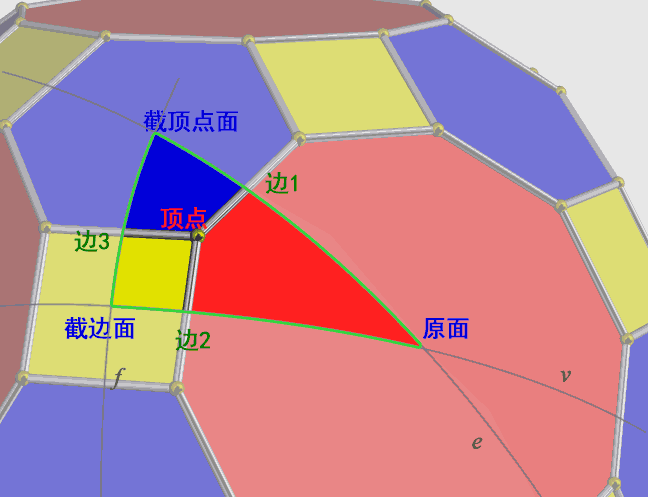
四维截角正多胞体
由于直接想象并绘制四维空间多胞体上的反射超平面太困难了，我们可以绘制三维正多面体镶嵌的基本四面体来寻找这些连接关系，它们与四维正多胞体的一样。从图中可得到四维截角正多胞体的各图元的链接关系表：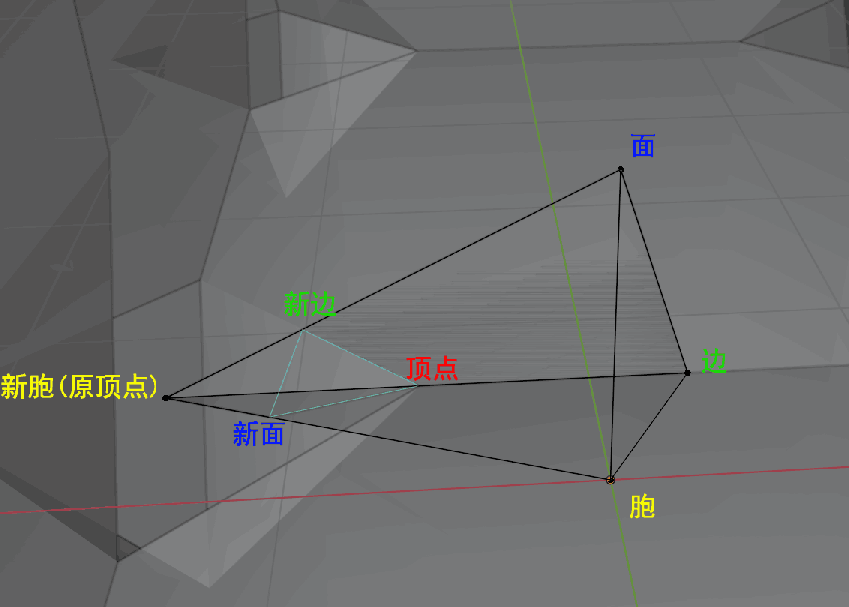
需要生成的连接关系：（其中(A+B)->C表示将表A->C与B->C合并）
- 边表：顶点->边、顶点->新边；
- 面表：新边->新面、(新边+边)->面；
- 胞表：新面->新胞、(新面+面)->胞。
四维过截角正多胞体
同理可得到四维过截角正多胞体的各图元的链接关系表。可能下图中新面2不太好看出来，它是截角截得的八面体越来越大，在边心碰面截半后，继续过截角，两个八面体相互挤压变成了截角八面体，新面2就是分隔两个截胞的那个“隔膜”，即截角八面体中的四边形面。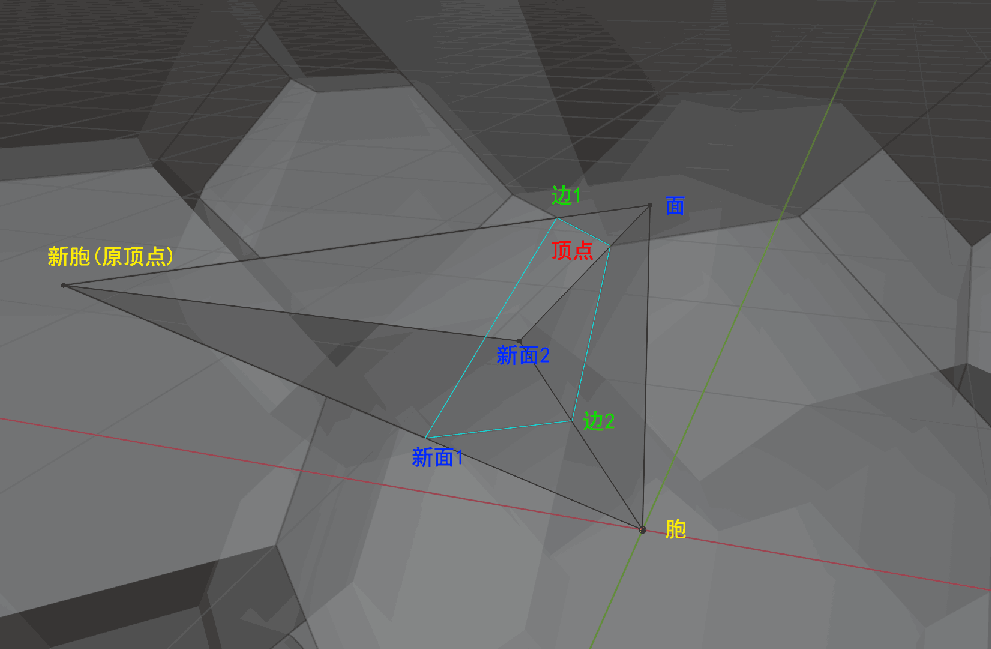
需要生成的连接关系：（其中(A+B)->C表示将表A->C与B->C合并）
定向胞腔复形
在渲染中，往往会将三角形按朝向相机的顶点顺序分成正面和反面从而实现背面消隐或给双面赋予不同材质。这很容易推广到使用四面体顶点指定的奇/偶排列顺序来区分四维空间中四面体胞的两种朝向，如何给一般的胞腔复形赋予定向呢？《同调论》中链群这节提供了思路：所有的n维面都有两种可能的方向，比如顶点有“正”与“负”两种状态，线段有两种相反方向，面可以根据组成它的线段的方向也有两种方向（暂且理解为顺时针/逆时针），体(胞)的定向则由它的面的方向决定。
具体怎样在计算机中记录呢？比如我们人为规定所有的顶点定向都为正，所有线段记录的两个端点中，第一个为正，第二个为负，所有多边形则可以规定沿边的指向顺序来书写，但对于三维胞的二维面则不存在任何有意义的顺序，不可能再利用顺序来确定定向。通用的方式只能是按从低维到高维按胞腔复形的构造方式来定义定向：某高维面的定向取决于它边界的定向。如果与默认的边界定向一致，则记作true，不一致则记作false，这样我们会得到一张全是布尔类型的定向表，比如下图是一个定向了的三棱柱：它的表面的“漩涡”方向从外面看都是逆时针。
顶点：{(1,1,-1)0,(-1,-1,-1)1,(1,-1,-1)2,(1,1,1)3,(-1,-1,1)4,(1,-1,1)5}
顶点表定向：{True0,True1,True2,True3,True4,True5}
边：{(0,1)0,(1,2)1,(2,0)2,(4,3)3,(5,4)4,(3,5)5,(1,4)6,(0,3)7,(2,5)8}
边表定向：{(True,False)0,(True,False)1,(True,False)2,(True,False)3,(True,False)4,(True,False)5,(True,False)6,(True,False)7,(True,False)8}
面：{(0,1,2)0,(3,4,5)1,(0,3,6,7)2,(1,4,6,8)3,(2,5,7,8)4}
面表定向：{(True,True,True)0,(True,True,True)1,(False,False,False,True)2,(False,False,True,False)3,(False,False,False,True)4}
胞：{(0,1,2,3,4)0}
胞表定向：{(True,True,True,True,True)0}
如果没看懂，这里再以2号面(0,3,6,7)2的定向来解释一下：顺着上图中蓝色2号面上的漩涡方向，它的边分别是0、7、3、6号边，这些边的方向与漩涡方向一致的是第四个7，它对应True，不一致的是前三个0、3、6，它们对应False，所以对应的定向为(False,False,False,True)2。
注意三棱柱只是确定了三维的定向，低维默认定向如何是无所谓的，下面展示了同样定向的三棱柱，但更改了某些一维（6号边）和二维（4号面）默认定向的数据结构：（改了定向的图元用黄色标出，因低维定向改动导致高维图元的定向组成改动用青色标出）
顶点：{(1,1,-1)0,(-1,-1,-1)1,(1,-1,-1)2,(1,1,1)3,(-1,-1,1)4,(1,-1,1)5}
顶点表定向：{True0,True1,True2,True3,True4,True5}
边：{(0,1)0,(1,2)1,(2,0)2,(4,3)3,(5,4)4,(3,5)5,(1,4)6,(0,3)7,(2,5)8}
边表定向：{(True,False)0,(True,False)1,(True,False)2,(True,False)3,(True,False)4,(True,False)5,(False,True)6,(True,False)7,(True,False)8}
面：{(0,1,2)0,(3,4,5)1,(0,3,6,7)2,(1,4,6,8)3,(2,5,7,8)4}
面表定向：{(True,True,True)0,(True,True,True)1,(False,False,True,True)2,(False,False,False,False)3,(True,True,True,False)4}
胞：{(0,1,2,3,4)0}
胞表定向：{(True,True,True,True,False)0}
实际设计数据结构时可以做一些优化，比如我们还是会按顺序来直接确定边与面的定向，用不着给顶点、边、面再单独记录定向表。
有了表示定向的方法，如何得到这些额外的定向信息呢？下面介绍生成定向数据的算法。
统一定向算法
很多时候，我们只能获得模型的基本数据，并没有定向信息，比如前面通过对称群的陪集枚举算法生成的正多胞体数据结构就不包含定向信息。在一个多面体中，其实只要我们指定了任意一个面的定向，其它面的定向也就随之确定。确定方法很简单：一条边在相邻面中的定向一定是相反的。利用这个原理，我们可以从已知定向的面出发逐步通过相邻面向外扩张确定其它面的定向。对于多胞体也同理:相邻两个胞的公共面在各自胞中的定向是相反的。
其实，只要胞腔复形具有局部的流形结构(即n-1维胞仅被2个n维胞共用)，定向就都能够通过刚才的传播算法确定，除了一种例外情况: 在莫比乌斯环或其它不可定向流形上，传播算法执行一圈后会发现前后定向不一致，渲染这些单侧曲面是无法做背面消隐剔除的。
统一定向算法其实是一股脑把模型建完后再赋予定向。如果在已知定向的图形上建模，怎样利用已有的定向信息用于确定构建出的新图形上的定向信息呢？下面以锥化与直积为例看下怎样处理定向信息。
锥形的定向
锥形的表面由底面与底面边缘锥化而来的侧面组成。我们将胞腔$A$的锥化记作$\widehat{A}$，设$\dim{A}=n$。注意，给定$n$维图形的定向后，它的锥化得到的$n+1$维图形的定向其实跟原图形并没有什么特殊关联，在此可以人为约定选择一个定向：选锥化后的$n+1$维体的底面与原$n$维图形定向相同，这样做是让不同维度的锥化操作都有确定的定向，以便递归地从低维向高维构建出定向的锥体。侧面的定向目前是不知道的，我们引入表示定向的未知系数$a$（只能取±1），它可能跟维度$n$有关，因此可记作：$$\partial(\widehat{A}) = A + a(n) \widehat{\partial A}$$边界一定是封闭图形，即边界的边界为0，所以两边再取边缘算子可得到$$0=\partial A + a(n) (\partial A + a(n-1) \widehat{\partial \partial A} )$$注意后面的$ \widehat{\partial \partial A}$也为$0$，因此最终得到$a(n)=-1$。
直积形的定向
我们知道直积形的表面有公式$\partial (A \times B) = \partial A \times B + A \times \partial B$，但这个公式完全没涉及定向，需要改造公式：加入表示定向的未知数$a $与$b$，它们均只能取$\pm 1$，且跟图形维度有关，设$\dim{A}=m$，$\dim{B}=n$，则这里的$a$、$b$其实是$m,n$的函数，即：$$\partial (A \times B) = a(m,n)\partial A \times B + b(m,n)A \times \partial B$$由于定向一定有两种选择，所以可以人为选择一个方向作为两个定向图形的直积形的定向的定义，这里我选择$b(m,n)=1$，即在直积后保持A图形的定向与原A图形定向一致，于是有：$$\partial (A \times B) = a(m,n)\partial A \times B + A \times \partial B$$边界一定封闭，即$$\partial^2 (A \times B) = 0 = a(m,n)\partial(\partial A \times B) + \partial(A \times \partial B)$$利用$\partial^2A=0$与$\partial^2B=0$，再注意$\dim(\partial A)=m-1$，$\dim(\partial B)=n-1$，可以化简得到：$$0 = a(m,n)(\partial A \times \partial B) + a(m,n-1)(\partial A \times \partial B)$$$A$与$B$可以是任意图形，因此要让等式恒成立就有$a(m,n)=-a(m,n-1)$，为了能让递推式能顺利进行，我们需要给出初值。当图形$B$为0维点时，我们希望它能像标量一样直接不改变图形A的定向，即$a(m,0) = 1$，这样我们就得到了$a(m,n)=(-1)^n$。
胞腔复形的单形剖分
我们在渲染篇中其实已经提到过将多边形分成三角形的算法：随便找一个顶点，将它与其它不相邻的顶点依次连线即可。对于多面体的四面体剖分，或更高维的多胞体的五胞体剖分（统称为单形剖分）该怎么做呢？我们可以用下面的算法：
剖分$n$维复形是递归的：首先，想要剖分$n$维复形，需要先剖分它的$n-1$维面。对于任意要剖分的$n$维胞，我们假设它的所有$n-1$维面已经被剖分成$n-1$维单形了，然后随便选取一点，通过胞腔复形的数据结构很容易查找出包含该点的所有$n-1$维面，我们忽略掉它们剖分出的单形，然后将该点与$n$维胞的其它$n-1$维面剖分出来的所有单形进行锥化操作成$n$维单形，即完成剖分。这个算法的思想就是多边形连对角线的推广，只不过要跳开那些与顶点共面的单形，避免剖分产生体积为0的退化单形。这个算法同样是可以保留待剖分胞腔的定向信息的：该算法只涉及到了锥化操作，而我们已经描述过如何处理锥化操作的定向使得锥形的定向与底面保持一致的了。
这里还想提醒的是：记录剖分后产生的单形信息不再需要边表、面表等结构，单形的所有顶点都是两两相连，每三个点一定形成三角面等特性让我们只用记录所有的顶点编号即可，而顶点的奇偶排列则完全决定了单形的定向，也不再需要额外的定向表，且渲染时进行背面剔除判断也很简单：只需要将要渲染的四面体的四个顶点的坐标按顺序组成行列式，从行列式求值的正负号就可知道四面体面对相机是正面还是反面。
四维网格图元格式
我们知道，一般的三维网格模型的基本图元都是三角形，然而很多建模师却偏好使用四边形来建模，这是因为四边形网格更符合建模布线的逻辑，类比到四维模型则是，模型的基本图元由四面体表示，然而一个立方体或一般的六面体需要剖分成五个四面体，因此直接支持处理六面体网格对于四维建模来说是相当必要的。不同于二维空间不存在复杂度介于三角形和四边形之间的多边形，除了四面体和六面体，三维空间是不是还会有其它的基本图元呢？。在我们的现实世界中很多工程需要使用有限元算法进行仿真计算，该算法会用到多面体剖分，就拿多物理场有限元分析软件COMSOL来说，它就内置了对四面体、三棱柱、四棱锥与六面体这四种基本单元的支持：(这里是COMSOL官方Blog对不同剖分的介绍链接)
这四种图元在四维建模中确实是给定一个由三角形或四边形组成的3D网格，将它锥化或柱化就将得到这四种图元。虽然目前Tesserxel仅实现了对四面体的支持，但我们完全可以仿照三维的wavefront obj（.obj）中的面储存格式，人为规定这四种图元的顶点顺序来表示记录胞（这样也能同时记录定向），通过这些胞来拼合成各种复杂的四维网格模型。
下面展示了一个传统的三维obj文件，它记录了一个三角形面和一个四边形面：
1 | # 井号开头行的是注释 |
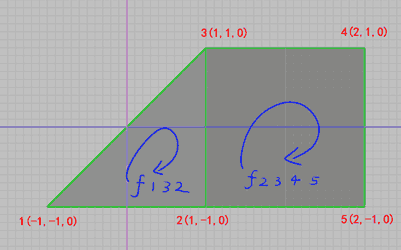
类似地，我们引入t表示四面体、tp表示三棱柱、qp表示四棱锥、h表示六面体，把下图的四个图元分别记作
1 | t 1 2 3 4 |
我们同样也能规定它们的定向：
- 在四面体所在的三维空间中，若用右手定则比出前三个顶点的顺序决定的该三角面的法线方向指向四面体的另一个顶点，则该四面体的法线朝向三维屏幕外，如果右手比出的法向背离第四个顶点则该四面体的法线朝向三维屏幕里；
- 规定先写出的底面三角形用右手定则比出的法线指向另一个底面则该三棱柱的法线朝向三维屏外，反之朝向三维屏幕里。
- 四棱锥前四个顶点是它的底面，还是看它用右手定则比出的法线是否指向剩下的锥点来决定法线朝向三维屏的里外方向。
- 六面体前四个顶点是它的底面，还是看它用右手定则比出的法线是否指向顶面侧来决定法线朝向三维屏的里外方向。
解释一下三维屏幕与右手的概念：首先要明确，“右手”指的是我们现实三维人的右手，因此需要先将“右手”放入四维空间中的三维子空间中。对于四维的观察者来说，三维子空间类似我们看一张平面，有前后两侧。四维人从一侧看上面绘制的三维人的“右手”图形，从另一侧看到的就却是镜像后的左手图形，这根你透过纸张从背面看文字法线都是反着的是一样的。也就是说右手的概念在四维空间中是相对的，因此，这里的定向含义是：如果从前面看到的是右手，法线法线朝外，而四维人绕至三维子空间另一侧，右手也变成了左右，此时再用右手定则得到的方向就是相反的，法线朝外也就变成了朝里，我们发现，法线方向与四维观察者在平面哪一侧是是无关的，因此这个定向是良定义的。从上图中可以看出，三棱柱的定向（向屏幕外）与其它三个（向屏幕里）是不同的。
好了，现在我们看似有了表示并存储任意复杂的四维模型场景的能力了，然而，事情并不是你想象的那么顺利简单。以上的所有讨论都建立要单形剖分的$n$维图形的所有顶点都是共$n$维超平面的，且它的每个$n-1$维的边界也应该是平的，即每个边界的所有顶点共$n-1$维超平面。如果我们绘制一些曲面图形，这些共面条件将很容易不再满足，按照上面的剖分算法会产生问题，下一小节我们就来讨论该问题。
剖分的合法性
我们现在的剖分算法遇到不共面的图形时还有一些小问题：比如我们分别四面体化了两个六面体，如果它们的公共四边形的四点不共面且两边三角化方向不一致，则剖分六面体后，四边形的不共面四点形成的四面体结构要么会重叠要么会产生中空的缝隙。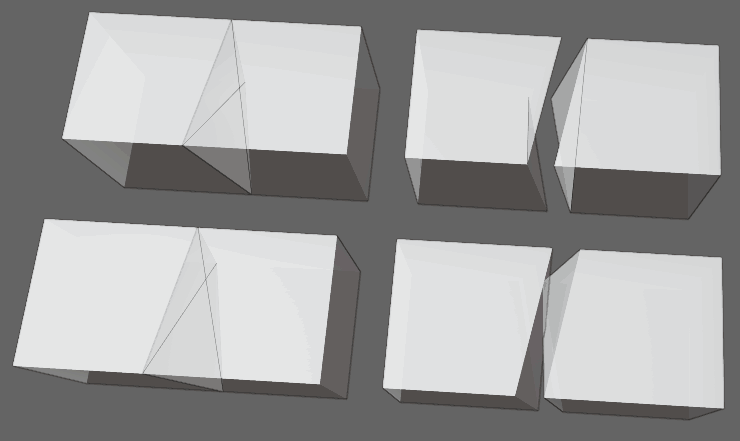
这些重叠和缝隙将影响渲染效果，比如Tesserxel中的猴头旋转体场景中就有这个问题还没处理。一个性质良好的剖分必须要在边界上保持一致。比如对于六面体网格，它的良好剖分模式应该采用下图右边这种交错式的方案，而不能采用相邻方块全都是同样方向的剖分方式。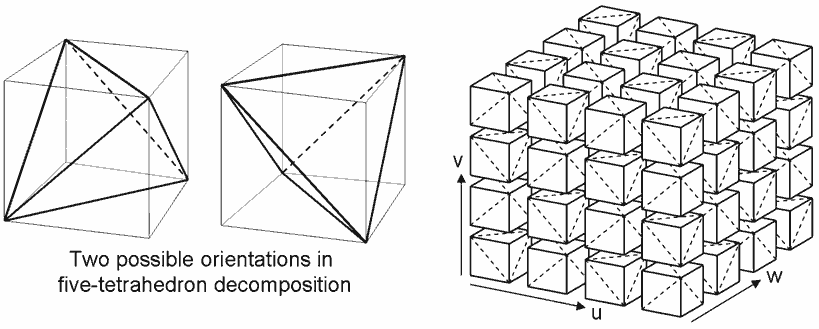
给定一个任意的四维胞腔复形，怎样得到符合上述要求的最佳剖分呢？遗憾的是这个问题没有多项式时间之内的算法，并且更可悲的是，有些凹多面体在不引入新顶点的情况下是不存在四面体剖分的，比如下面这种每个侧面都向同一个方向剖分对角线的扭棱三棱柱，叫做Schönhardt polyhedron。
上面那个例子也说明，给定三棱柱侧面的一种剖分不一定存在合法的三棱柱剖分，比如下图三棱柱侧面一共有$2^{3}=8$种剖分方式中，只有绿色的剖分才是对应可行的三棱柱剖分。
六面体的情况则更多了，每个面两种剖分方法组合下来就有$2^{6}=64$种可能性，其中下图a）至e）46种情况合法，存在剖分；f）g）18种情况为非法，即找不到相应四面体剖分。判定剖分的合法性看似复杂，其实有些技巧捷径：若存在三个对角线汇集在一个顶点则一定是合法剖分，因为我们能选该顶点通过那三条对角线跟其它的面连线来把六面体先分成三个四棱锥，而四棱锥的任意剖分都是合法的。然而这个条件不是充要的，b）就是唯一的例外。证明不存在合法剖分也很简单：若存在剖分，则六面体表面的三角形一定是剖分出的四面体的一个面，我们可以通过对角线方向的一致性与顶点不能共面的条件寻找四面体的第四个顶点，如果无法找到，则不存在合法剖分。
注意所有合法剖分里面只有a）两种剖分产生了5个四面体，是最优的，其余方案则均产生6个四面体，在保证剖分合法的前提下，我们应该优先选择更少的剖分从而降低后续渲染的面数。
最后，四棱锥是最简单的，它的两种剖分都是合法的，都产生两个四面体。
对于一个四维网格模型，它可能由这几种基本胞腔图元混合拼合组成。为了让胞腔之间的四边形不会因顶点不共面产生重叠或裂缝，我们必须直接先给每个四边形指定按哪条对角线剖分，然后确保每个胞腔都是合法剖分即可。具体可通过贪心算法的策略来寻找满足条件的剖分方案：由于六面体遇到非法剖分的机率最大（前面每个图注中都有统计），因此首先优先选取一个最优剖分来剖分六面体，然后再逐渐确定相邻胞腔的剖分。如果相邻胞腔有多种类型，我们均按照六面体、三棱柱、四棱锥的优先级剖分，同一个胞腔的多种剖分除了六面体优先选择两种最优剖分外其余则没有优先级，只能随机选择，如果某一步发现目前所有的方案都存在非法剖分，则回溯并改变上一步的剖分方案再去尝试。
Youtuber Codeparade在开发游戏《4D高尔夫》中的树木模型时也发现了空间四边形的不同剖分会引起缝隙的问题。他指出只针对柱体合法剖分的问题是NP完全（NP-Complete）的：若三维底胞是全由三角形构成的二维网格，则这些三角形将柱化成三棱柱，每条边柱化成了三棱柱侧面的矩形，每个矩形都有沿两条对角线三角化的方法，然而之前我们已经说到有些方案是不存在四面体剖分的，Codeparade将对角线选择问题转化成了等价的图论中经典的双色染色问题从而证明了NP完全性，具体细节可以参考他的视频。从这些例子大家可以窥见任意胞腔复形四面体剖分问题的困难程度，对于任意图形哪怕放弃最优剖分，只是想找到合法剖分也不是一件简单的事情。本文只是分析了六面体、三棱柱和四棱锥，对于任意的三维胞腔，剖分它们显得更加寸步难行：如何剖分120胞体上的十二面体，使得正120胞体模型顶点加入一些扭曲噪声后不让不共面的二维图元之间产生缝隙？四维隐函数方程得到的三维胞的二维面一般都不共面，且形状各异，又如何防止缝隙？好在事情并不是那么糟，还是有最笨的保底策略：对于二维面，我们随意将其三角化即可；对于三维胞，选取胞心点为顶点，跟所有剖分的二维面产生的三角形连接成四面体就一定没问题，说它“笨”体现在需要额外引入新顶点和更多的四面体。