特色内容
本文目录:
旋转体
上一篇文章中,我们看到了直积图形双圆柱和一些圆环的类比。里面充斥着很多“圆形”的东西,一般圆形都是由旋转而来的,我们下面就来从旋转体的角度来看看四维空间的那些我们已熟知和未知的几何体。
圆柱柱作为旋转体
大家都知道矩形绕一条边旋转得到圆柱,那圆柱柱能由什么旋转而来?我们分析圆柱:它的底面是圆,圆当然由线段绕端点旋转而来,柱体则把线段“拉”成了矩形,把旋转点“拉”成了旋转轴。那么圆柱柱就是矩形升级,“拉”成长方体,绕着一个面旋转。
面稍微远一些?
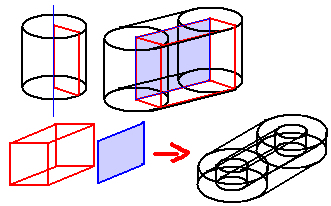
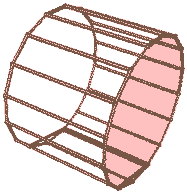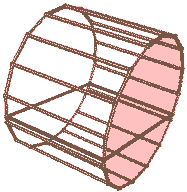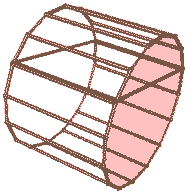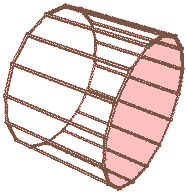
我们把旋转面稍微平移一下,使之离长方体有一定距离,我们将得到“圆环柱柱”(圆环和长方形的直积)。这里的圆环是二维的那种两个同心圆。当圆环内径为0时就变成了上一种情况:圆柱柱(圆和长方形的直积)。
旋转圆柱、球
大家思考一下:我们在四维空间中旋转圆柱和球会得到哪些几何体?当然圆柱不是高度对称的几何体,我们可以取以底面、过对称轴的平面、平行底面与圆柱有一定距离的平面、平行对称轴与圆柱有一定距离的平面等作为旋转平面,会得到不同几何体。(当然还可以选斜着的任何面,但得到的不规则图形意义不大)我们来看圆柱绕底面旋转的情况:由于四维空间中的旋转十分抽象,我们是无法直观想出旋转过程的,现在只能通过“截面动画”法“降维”。具体怎么降维呢?假装没有直接想象三维圆形旋转体图形(即圆环)的能力,我们可以这样做:
 |  |
下面是圆柱绕它的底面旋转的情形:
|
|
|
看,右边的截面动画说明这个几何体是双圆柱!其他选取旋转平面的情况留给大家思考,我会在文章最后公布答案。
球绕它外面的平面旋转得到球环,这是球环最原始的定义,而球绕过球心的平面旋转得到超球(想想圆的情况不难理解)。为什么不让球绕不过球心的但与球相交的平面旋转呢?因为这个图形是自相交的(依然想想圆的情况,那个东西像个苹果),我不认为自相交的图形是良好的。
旋转圆环
我有四种比较“规矩”(不选斜的)的选择旋转平面:其中不与圆环自身相交的两种平面上次都讲过了,还有两种特殊位置上的平面:
- 过对称轴的平面:我们也提到过旋转后得到球环。
- 垂直对称轴的圆环的对称面:留作思考题,答案见文章最后。(提示:可以从想象截面动画入手)
圆柱锥、圆锥柱、圆锥锥作为旋转体
其实在圆柱柱那里我们已经发现了一个规律:通过“柱体”把旋转体“拉”到高维时,它的旋转“单元”也被“柱体化”了,锥体也一样。所以圆柱锥是一个四棱锥绕侧面三角形旋转而来,且这个侧面垂直于蓝色底面长方形。(我们讨论三维图形,垂直就是二面垂直;别忘了四维空间还有绝对垂直)
同理,圆锥柱是三棱柱(蓝色三角形被“柱”化)旋转而成的,圆锥锥是三棱锥(蓝色三角形被“锥”化)旋转而成的。(下图红色为旋转面)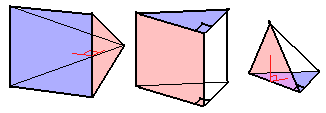
返回目录
放样体
我以前用过3dMax这样的三维软件,有一种建模方法叫“放样”(lofting):将一个二维形体对象作为沿某个路径的剖面,而形成复杂的三维对象。
比如柱体可以看底面作为横截面沿直线放样,圆环可以看成横截面圆沿另一个圆放样。四维空间当然也有放样:我们把三维截面沿直线放样就是四维柱体,沿圆放样就是旋转体,沿其它曲线放样能得到更多更复杂的四维物体。但与三维不同的是,四维还有“二维放样”:我们把二维截面沿一个二维曲面放样!二维曲面是平的就对应直积,是弯曲的就复杂了,我们只见过圆环的一种旋转体——环球——它是横截面圆沿着球面的放样体。如果四维文明也有类似4D建模软件的话这肯定是很好的建模方式。
我想四维文明使用的管道、公路大概都是放样体吧。
四维分形
Mandelbrot-Julia集
看了《维度》第6集——分形,唯一给我的就是震撼。我们现在要把那两个神奇的集合——Julia集和Mandelbrot集在四维空间中统一起来。
Julia集的定义就是在复平面上给一个数$z$,然后你不断做运算:$z\to z^2+c$($c$是固定的复数),最后你的$z$很可能算到无穷大,那些所有不会算到不是无穷大的初始的$z$值就在复平面上构成Julia集。当然Julia集的形状随复数$c$的变化而变化。试想你把$c$取上个10000,随便取哪个$z$进去算都绝对会越平方越大,即到无穷大,所以$c=10000$时的Julia集为空集。那些所有Julia集不是空集的$c$的集合组成了Mandelbrot集。(挺绕的)
有定理保证,只要一个Julia集在$z=0$时都是发散的则它一定是空集,所以Mandelbrot集又可以定义为:取初值$z=0$做迭代运算$z\to z^2+c$不发散的$c$的集合。
$z$是一个复数,$c$也是一个复数,我们可以得到一个复数对$(z_0,c)$,定义:若取初值$z=z_0$做迭代运算$z\to z^2+c$不发散,则复数对$(z_0,c)$属于集合$P$。注意这个复数对其实描述的是四维空间$(x,y,z,w)=(Re (z_0),Im (z_0),Re (c),Im (c))$,则我们的julia集可以看作是四维空间中的集合$P$被面$z=Re(c),w=Im (c)$所截得的图形,Mandelbrot集则是集合$P$被面$x=0,y=0$截得的图形。我们叫集合$P$为Mandelbrot-Julia集(非官方名称)。
Mandelbrot-Julia集高度不规则,我们无法直观看到它(球极投影就不可能了),不妨看看它被6个坐标面截得的截面:
$xy$面: | $xz$面: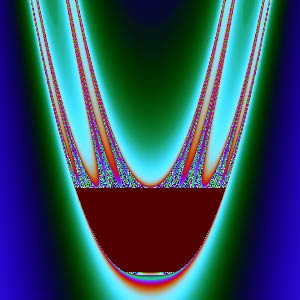 |
$xw$面: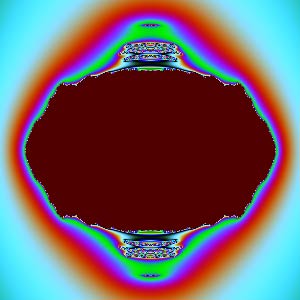 | $yz$面: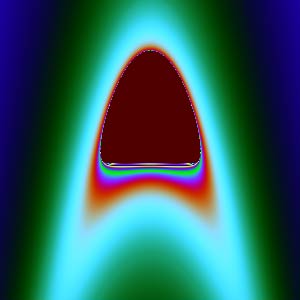 |
$yw$面: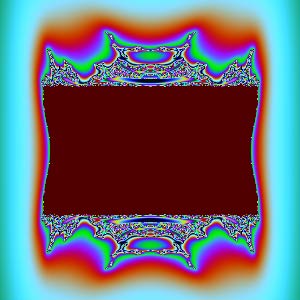 | $zw$面: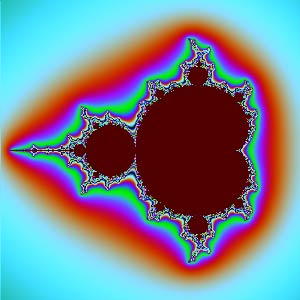 |
除了$xy$、$zw$截面,其他截面怎么那么“难看”?它们放大后看不到更细腻的图形,像是被“撕”成了不规则的丝状。复数变换能产生精美图形的秘密就是:它们都是共形(保角)变换。共形能够保证微小的图形保持原样,不会出现“丝状撕裂”。$xy$平面刚好是复数$z$的实部虚部,那个圆正是$c=0$时的Julia集。$zw$平面刚好是复数$c$的实部虚部,对应Mandelbrot集。但$xz$、$xw$、$yz$、$yw$是两个复数之间分量的组合,一旦我们这样割裂开来看复数,它们就没有内在联系了,共性形也没有了,所以图像会很难看。
我们现在旋转Mandelbrot集所在的$zw$平面转到Julia集所在平面,截面就能缓缓地从Mandelbrot集过渡到Julia集!但别忘了截面过原点的Julia集只是一个圆($c=0$),所以还要同时叠加一个平移变换。为了杜绝旋转中的“丝状撕裂”,我们得选让复数$z$和$c$地位相等的平面——与$xy$平面、$zw$平面等角的平面!前面对纤维丛介绍中说过,等角平面(同手性)的集合与纤维丛中的圆一一对应,所以也和一个球面上的点$k$一一对应(这里有$z=k c$)。我们把Mandelbrot集平面放在南极,则与它绝对垂直的Julia集就在北极,过渡动画需要选一条从南极到北极的路线,但这有无数条——所有经线都连接两极。选择不同的经线我们就能得到不同的过渡动画,我这里选的是本初子午线(其实没有规定死0经度的位置):

其它
四维分形直接可视化本来就几乎不可能,但我们还是能猜想一些四维生物会喜欢的分形。 比如著名的Cantor三分点集的二维推广在平面生物看来没什么意思:它们看不到那些在内部的空心正方形,它们可能喜欢类比成右边这样:
比如著名的Cantor三分点集的二维推广在平面生物看来没什么意思:它们看不到那些在内部的空心正方形,它们可能喜欢类比成右边这样:
 |  |
但对我们三维生物来说,右边那种分形几乎快“碎成渣”了,还是中间的谢尔宾斯基地毯看起来顺眼。
三维空间就对应三种类比了:一种也是我们看起来几乎快“碎成渣”的“门格-谢尔宾斯基雪花”、还有一种是经典的门格海绵,另一种则是四维空间生物喜欢的:将正方体掏空、掏空再掏空。但我们看不到正方体内部,就像二维生物一样无法欣赏谢尔宾斯基地毯一样。


四维这种分形类比应该能分成4种:碎成渣的、门格海绵这种千疮百孔的、挖很多三维孔的(这些孔在四维空间中是连起来的)和四维生物都无法欣赏到的中空超立方体洞。
Mandelbrot集的三维比较好看的类比是Mandelbulb,四维中我们可以用四元数(复数的4维类比)来造分形但共形性很可能保持不了可能只能用四维极坐标(算法:强行平方距离坐标,翻倍角度坐标)而放弃四元数了,但不管怎样,我相信Mandelbulb4D应该会更加好看,
返回目录
二次曲胞
大家都应该知道二次曲面吧:抛物面、柱面、球面、双曲面、锥面、马鞍面等等。之所以叫“二次曲面”那是因为它们的方程是二次的。三维空间中就是三元二次方程,四维当然是四元二次方程。涉及到方程,显然就是代数问题了,所以我尽量多给出一些关于二次曲胞的感性的结论而不是推导过程。
三维空间中有这么多二次曲面,这是怎么分类出来的呢?这就要涉及到标准二次型的问题了。这个我们不详细讨论,下面只给出分类方法:
我们总能建一个坐标系,使大部分曲面在坐标系里的方程变为$ax^2+by^2+cz^2=d$
且不管我们找的什么坐标系方程都有同样数目的正项和负项,我们就可以用这一指标对曲面(胞)分类。所以对三维空间有:
| 正项个数 | 负项个数 | 常数$d$符号 | 名称 |
|---|---|---|---|
| 3 | 0 | + | 球面 |
| 3 | 0 | 0 | 一个点 |
| 3 | 0 | - | 无解 |
| 2 | 1 | + | 单叶双曲面 |
| 2 | 1 | 0 | 圆锥面 |
| 2 | 1 | - | 双叶双曲面 |
注意正项比负项个数少的情况与前面重复了,方程两边同时反号后就一样了。我们这里只列举了系数相等的情况,椭球、椭圆抛物面等只是上面情况的缩放变换,这里省略不写)
但好像我们还漏掉了一些面:它们方程中有一项不是二次的:要么根本没有(柱面:圆柱、抛物柱、双曲柱)或为一次项(抛物面、马鞍面)。
根据这个思路我们来看看四维空间中的二次曲胞:
| 正项个数 | 负项个数 | 常数$d$符号 | 名称 |
|---|---|---|---|
| 4 | 0 | + | 超球面 |
| 4 | 0 | 0 | 一个点 |
| 4 | 0 | - | 无解 |
| 3 | 1 | + | 单叶双曲胞 |
| 3 | 1 | 0 | 球锥面(光椎) |
| 3 | 1 | - | 双叶双曲胞 |
| 2 | 2 | + | “直积”双曲胞 |
| 2 | 2 | 0 | “直积”双锥胞 |
它们方程中有一项不是二次的:要么根本没有(柱面:这里不罗列了,所有三维二次曲面都能“拉”成柱体)或为一次项。我们重点讨论一次项:在一次项出现时常数项能够通过平移消掉,也没有同时两项一次项同时出现,同样选择合适坐标系能只剩一个。所以我们的表格很简单:
| 正项个数 | 负项个数 | 名称 |
|---|---|---|
| 3 | 0 | 旋转抛物胞 |
| 2 | 1 | 马鞍胞 |
下面我们来具体介绍我们不熟悉的图形:
超球是四轴椭超球的特殊情况(类似球与三轴椭球)
单叶双曲胞(类似单叶双曲面)它有一个对称轴。注意一般四维空间只有对称面(类似三维对称轴),这里的对称轴相当于球对称(类似三维点对称),单叶双曲胞垂直于对称轴的截胞都是球。
双叶双曲胞(类似单叶双曲面)它也有一个对称轴,它垂直于对称轴的截胞也是球,但注意它由独立两部分曲胞构成,像双叶双曲面那样,截胞处在两“叶”之间时什么都截不到。
球锥面:它也是轴对称(球对称)图形。它的垂直轴的截胞动画是一个球半径均匀缩小成一个点再均匀变大。相对论里面的光椎就是球锥!(均匀变大的球对应可观测宇宙的膨胀,球体体积就是哈勃体积)我们的主题是空间,而不是时空,所以我们就不展开了。
“直积”双锥胞:这个图形有点抽象,但还好。我们看它的标准方程:$x^2+y^2=z^2+w^2$ 有没有一种熟悉的感觉?如果我令$x^2+y^2=z^2+w^2=1$,这就是双圆柱的两个曲胞的交面方程。即“直积”双锥胞和超球相交,交集投影下来就是那个圆环面!它高度对称:它有对称面$xy$、$zw$,其实所有与$xy$、$zw$等角的平面都是对称面。但截面动画无法给我们更多信息。
“直积”双曲胞:这个图形更抽象,但“直积”双锥胞绝对是“直积”双曲胞的“渐进三维面”(直积双曲胞的常数趋于0就得到“渐进三维面”,想想双曲线的渐近线和双曲面的渐进锥面)。但截面动画也无法给我们更多信息,欢迎大家提出更好可视化它的方法。
旋转抛物胞:也是轴对称(球对称)图形,可看成抛物面绕它的对称面得到的旋转体。
马鞍胞:方程:$x^2+y^2-z^2=w$ 它是一个函数:一个三维坐标$(x,y,z)$对应一个数$w$。马鞍面是一个方向凹(凸)另一个方向凸(凹)的,但四维空间反而没这么好的对称性:是一个方向凹(凸)另两个方向凸(凹)(一个平面上)的。但这样描述还是很抽象,欢迎大家提出更好的可视化方法。 这里CFY使用截面法展示了几种二次曲胞。
思考题答案
过圆柱对称轴的平面作为旋转平面得到球柱。
平行底面与圆柱有一定距离的平面作为旋转平面得到二维圆环与圆的直积。
平行对称轴与圆柱有一定距离的平面作为旋转平面得到圆环柱(三维圆环与一维线段的直积)。
垂直对称轴的圆环的对称面作为旋转平面得到球环。