注意,这篇文章中的有些内容纯属想象,里面有很多漏洞,不要当真。
大概内容
- 天体力学
- 地理及交通
- 常见建筑、物品及文字
- 机械运动
- 四维空间中的电磁场
我们对四维几何体已经有了比较全面的了解。现在试想有一天你被邀请去参观四维国,并了解他们的文化与科学技术这会是怎样的一番体验?
在浩瀚的四维宇宙中,零星散布着一些星系。你要参观的那个星球就在某一个星系当中。那个星球是一个超球,它也绕着一颗恒星旋转。但由于多了一个维度,根据“高斯定理”,恒星引力将随距离立方反比衰减。你可能觉得这没什么,但计算可得,这将会导致行星运行轨道极其不稳定:要么坠毁要么飞出星系。
你要去的这颗行星是一个奇迹——它的轨道几乎完全是个正圆!这颗行星上的文明已经有一万年历史,他们夜晚的天空上只看得见几颗很暗的星星。因为如果近处有天体,就将打破行星在圆轨道上的运行。一万年以来,这颗行星上的科学家在他们计算精度范围内算不出它的轨道与正圆形有偏差,但在四千年前新的测算结果显示这颗行星偏离了圆轨道,或许再过一千年就会离开恒星。科学家们后来只好通过几次小型核爆修正了这点轨道上的微小差异。修正后的轨道可以满足行星再运行一万年以上。
这个世界中有繁华的城市和街道,也有森林、高山与海洋。他们早就绘制出了世界地图,他们使用二次墨卡托投影——先把超球面投影到球柱面上,再投影到圆柱柱面上,最后展开得到一幅长方体地图。没错,他们使用的所有地图都是三维的。在地图上,它们的河流看起来像空间中的有粗细的曲线,湖泊是一个立体的图形,他们从来不会遇到过河这件事:在三维中完全可以绕着空间曲线走,所以除了专门去河上钓鱼,你是找不到一条建在河上的道路的。但这并不代表山区就不用修桥:河床冲出的线状山沟确实能绕着走。但如果遇到湖泊或三维洼地或二维的断裂面就必须要修桥了。但盘山路、隧道还是躲不过的。我想隧道的截胞形状应该是球体吧。
在城市里面交通拥堵对他们来说根本就不是个问题。路口也不用修立交桥,车流量大的主干道还可以修成二维的!(它们的广场都是三维的)当然他们的路其实都是四维的,只是在地图上没标高度,且忽略路的宽度,才说路是一维或二维的。
至于公路的截面(不是截到露出地基的那种截胞)是什么形状的这个我们完全没有经验——我们的二维公路截面就只是一条线,它的长短代表路宽。上面我画的路的截面是圆形的,但如果是双向车道感觉这种设计也不是太好。我也不知道哪种截面的路最好,但从隧道的截胞形状应该是球体推出隧道里面路的截面是圆形的好一点。
注意,这些他们看似能在三维中随意行走的能力并不代表他们能飞行,他们都是“脚踏实地”地站在他们的星球上的。这个世界中一般的房间都是超立方体结构的,当然不排除设计师修建圆柱柱或球柱房间……水管一般是球体放样体,(直的水管就是球柱)Hopf纤维丛是他们最常见的几何艺术形式,常常拿这些图案刻在超球珠子上卖。他们的项链都是些打孔的小超球串起来的,但还有一种球环的首饰也很受欢迎:用线把我们三维球体的二维球壳(记上厚度就是球环)穿在一起。他们的衣服都是三维的面料!他们也从来不会纺织:四维空间绳子无法打结,我们三维空间中一件好好的毛衣拿去一扯就变成一根线了。当然这也有好处:他们放风筝时线永远不会缠在一起。至于交通工具汽车,它们不能只有4个轮子了,这样车是不稳的,另一侧会着地(想想你的三维车只有左侧有前轮、后轮,右边就拖地上了)。所以你将看到四维汽车有8个轮子。当然我们其实也有三轮车这种简易的交通工具,对于他们来说,如果能稳着不倒,四个轮子是四维车必须的。当然这里轮子的形状不是圆柱或三维圆环了,我觉得是球柱或环球。但球使得控制方向成了问题,所以他们可能还会把前轮做成圆柱柱(或圆环环)。自行车?用两个球或两个圆做轮子骑起来估计都不会倒,但球形轮子无法控制滚动方向,所以估计还是用两个圆形的轮子好些。他们去远的地方还是要坐飞机,因为地面虽然交通畅通,但弯道和摩擦都是存在的,也有最高限速。
说起四维空间中的“圆”的物体的滚动,简单的有超球、球柱、双圆柱、圆柱柱这四种。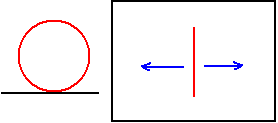
- 三维空间里平放的圆柱在2维桌面上,这种摆放方式决定了滚动方向是唯一的:垂直于它的旋转轴(即高),即垂直于它与桌面的交线。若硬要沿着交线移动,这就是摩擦打滑了。
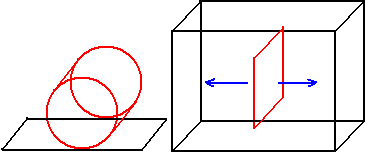
- 四维空间中圆柱柱平放在3维桌面上,滚动方向也是唯一的:垂直于它的旋转平面(它平行于与桌面的交面),若硬要沿着它与桌面的交面移动,这也是打滑了。
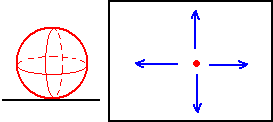
- 球柱平放在3维桌面上可以在垂直于它的高的平面里任意滚动,就像球体放在桌子上那样滚动。
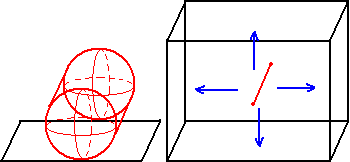
- 超球可以在3维桌面上任意滚动
- 双圆柱虽然有等角旋转对称性,但是放在3维桌面时只能把一个曲胞放置与桌面相切(相切于一个圆),导致它只能向垂直于相切圆的方向滚动,也就是说它的滚动性质和圆柱柱是一样的,只是不参与滚动的侧面圆柱柱是方形,双圆柱是圆形。总的来说,圆柱柱双圆柱能朝一个方向滚动,球柱能在2维平面上自由滚动,超球可以在3维的胞中任意滚动。
(更新:基于4D刚体力学的滚动模拟器做好了,戳这里!)
这个世界中引力、电磁力都是立方反比衰减的。所以为了应对衰减过快的困难,他们的路灯修建得比我们的更密集;但他们的电路板、芯片也是三维的,所以信息技术非常发达。我们知道三维空间中锥形齿轮用于相交轴间的传动。与柱形齿轮相比,能够改变传动方向。到了四维空间,只需要给它们都加点“厚度”:锥柱形齿轮用于相交轴间的传动。与柱柱形齿轮相比,能够改变传动方向。但这个传动方向的改变还是在一个三维空间中。我们怎样设计一套装置使得$xy$平面上的运动能传到$zw$平面上去呢?我们可以用两套锥柱形齿轮,第一套负责把$xy$平面上的运动转到$xw$平面上,第二套再把$xw$平面运动转到$zw$平面上。但这个方法有点笨拙,四维文明肯定发明了一步到位的传动零件。(我想不出来了)
四维文明的文字是不是三维的?如果是,它们是由曲面构成还是由空间曲线构成?我认为首先它们都会选择三维文字,但不同的四维文明都有自己不同的习惯选择用线还是用面。从方便性来说,空间曲线是最好“写”出来的了。但他们肯定会遇到画线、面、胞等情况,笔还得换。因为你肯定不想用画空间曲线的笔来涂满整个三维胞吧。所以它们有专门画面的笔(可能像把刷子),用这种笔填三维胞工作量就小多了(就像我们用一般的笔涂一个区域那样)。想画直线/平面?那还得借助各种维度的尺子才能画平直。
一点物理猜想
有科学家发现了光速不变和相对论,还提出了“五维时空”的理论!其实这些和我们四维时空的性质都大同小异。但唯一例外的是他们的磁场:磁场不再是矢量,而是2-向量。最简单的情形是放一根通电导线发现平行于某一平面时受到的“安培力”最大,平行于某一平面的绝对垂直面时不受力的作用。当然很多时候2-向量不是简单的,这时导线在任何取向下都会受到磁力!三维空间对应的四维时空中的电磁张量(其实也是个2-向量)长这样:$$F=\begin{pmatrix} 0 & E_x/c & E_y/c & E_z/c \\ -E_x/c & 0 & -B_z & B_y \\ -E_y/c & B_z & 0 & -B_x \\ -E_z/c & -B_y & B_x & 0 \end{pmatrix}$$我猜四维空间对应的五维的电磁张量(2-向量)长这样:$$F=\begin{pmatrix} 0 & E_x/c & E_y/c & E_z/c & E_w/c \\ -E_x/c & 0 & B_{xy} & B_{xz} & B_{xw} \\ -E_y/c & -B_{xy} & 0 & B_{yz} & B_{yw} \\ -E_z/c & -B_{xz} & -B_{yz} & 0 & B_{zw} \\ -E_w/c & -B_{xw} & -B_{yw} & -B_{zw} & 0\end{pmatrix}$$
四维世界系列
这个世界不同于之前讨论的几何学或代数学,它包含物理等更多设定,所以客观性真实性大打折扣。但四维世界很精彩,我建立了一个独立于四维空间系列的新系列:四维世界系列来探索这个充满着未知的地方。