
《维度》系列的最后一集是一个预告片:Dimensions II ——它的内容不是后来出的《混沌》(chaos),而是《维度》制作者之一——数学家Étienne Ghys的最新研究成果。这些内容就更深奥了,我估计他们可能不会出这集了。我在《维度》另一个制作者Jos Leys的网站上找到了介绍预告片中出现的图形(即Étienne Ghys的最新研究成果)的文章:
这里是我做的格子空间4D在线查看器
(我一直很奇怪我画出的modular动力系统的轨道与判别式三叶结为什么会靠得很近,检查了很多遍代码都没找到原因)
大家感兴趣还想深入下去可以看一些关于椭圆函数、模形式的书,建议参阅潘承洞的《模形式导引》(网上有pdf,我前三章还能看懂,后面就看不懂了)
下面是我在阅读这篇文章遇到的一些难懂的地方的理解和补充。
洛伦兹吸引子
若无法理解或想了解关于洛伦兹吸引子更多的信息,请看《维度》制作者的另一系列视频:《混沌》。真的要定量分析的话肯定涉及到大片大片公式推导,我们这里就不讨论它了。
Seifert曲面
Seifert曲面非常有意思:它指的是以扭结或链环为边界的曲面。比如Hopf链环上的Seifert曲面(Hopf link):
曲面分单侧曲面(不定向)和双侧曲面(定向)。单侧曲面最著名的例子就是莫比乌斯带。莫比乌斯带的边界是一个圆,当然,圆可以看成平凡的扭结。所以,以圆为边界的Seifert至少有两种: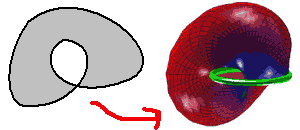
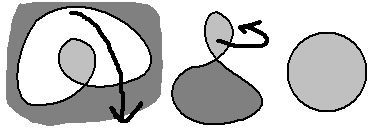
其中我在扭结外面涂上颜色是指这个曲面像一个从内部看一个有孔的气球一样,把它翻下再扭半圈去就得到了普通圆片。
我们再来看三叶结:我们有这几种Seifert曲面:注意右边两个也是三叶结,只是投影方式不同,后来构造“模板”时$\Delta =0$曲线的样子就是这样的。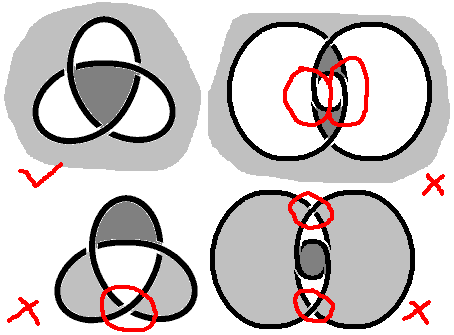
我们可以用涂色法来判断这些Seifert曲面是否为单侧曲面:扭结的每一个“交点”处的曲面看起来被扭转了180°,所以过一个交点后正面、背面应该交换,如果我们能相间隔地用两种颜色(正反面各对应一种)涂满曲面,说明就是双侧曲面,否则就是单侧的。
通过这种方法我们发现只有第一种曲面是双侧的——它就是Josleys文章里在四维空间中的曲面!
矩阵
modular动力系统中的格子动画是最精彩的了。要看懂文章中对这个构造的具体描述,你首先得有线性代数矩阵的概念、特征值、相似矩阵的概念。这些概念并不复杂,可以在网上或任何一本线性代数书上找到。我唯一想提的就是模矩阵分解成U、V矩阵的方法:一个矩阵左乘U矩阵或V矩阵对应着这个矩阵简单的列变换:把一列加到另一列。所以我们倒过来做:每次操作都是大列减小列,总能到单位矩阵。如果是右乘则对应行变换,最后也能求出分解成U、V矩阵的式子。
格子空间结构图
$g_2$、$g_3$是描述格子的核心参数,它们在模形式理论中也是很重要的量。但它们的定义都是对格点无限求和的形式,要搞清楚它们似乎要涉及复杂的高等数学运算。我们不打算涉及太多这方面内容,下面我们从文章中给出的现成线索最大化地了解一下格子空间中的点到底对应了哪些格子:
首先,文章中提到了$g_2=0$和$g_3=0$这两个圆,它们分别是正方形格子和正六边形格子。然后我们还有一个黄色的三叶结对应$\Delta =0$的曲线。文章中还告诉我们,$\Delta =0$时$(g_2,g_3)$不和任何格子对应,这说明在$\Delta =0$的曲线附近一定有什么发生。计算可得,如果一个格子很“扁”,它的$|\Delta |$就会非常小,如果无限扁,它的$\Delta =0$,当然无限扁是不存在的。
为什么$\Delta =0$对应一个三叶结?
一般我们旋转一个格子半周格子就和原来重合了。这个过程中参数$g_2$在复平面中以四倍角速度在旋转(因为g_2的定义式里有格点4次方,幅角乘4),$g_3$在复平面中以六倍角速度在旋转,这两种旋转合成了格子空间中的总运动:不等角的双旋转。CFY的这篇文章已经分析过这种运动了,它的轨迹就是三叶结。
这种运动使四维球面中充满了三叶结,这些三叶结与两个圆周($g_2=0$、$g_3=0$)填满了整个四维超球,我们又得到了一种纤维丛!
从这里我们看到无限扁的格子也被当成了普通格子旋转,它只是纤维丛中看起来一个很普通的三叶结。
现在我们在两个视图中标一下我们已知的结构: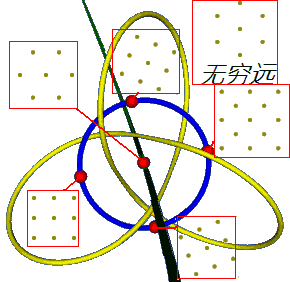
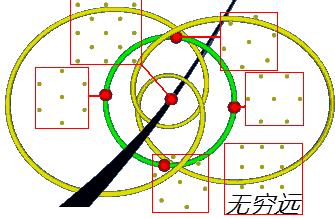
文章后面在构造“模板”的时候给了我们一个信息:所有正六边形格子所在的圆($g_3=0$)的某一条直径都是一些对角线水平的棱形,且顶角在60°到120°之间变化。那如顶角超出60°到120°这个范围这些点会在哪?我们猜想把这条直径延伸出去就对应那些点。无限延伸?我们会“撞”到$\Delta =0$这条线:它对应着顶角为0°和180°的很扁的棱形。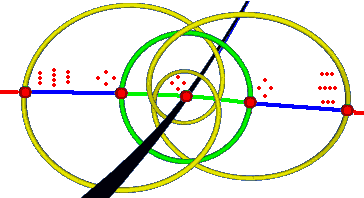
如果我们穿过$\Delta =0$继续延伸,最终会延伸到无穷远:那个点对应着正方形格子。从$\Delta =0$到无穷远对应着无限扁的棱形到正方形格子,这个过程又是怎么回事呢?其实穿过$\Delta =0$的瞬间,格子已经从棱形变成了矩形!因为无限扁时你已经分不清矩形和棱形了。红色延长线对应矩形的压缩与拉伸。
让我们换另一个视角看这条延长线: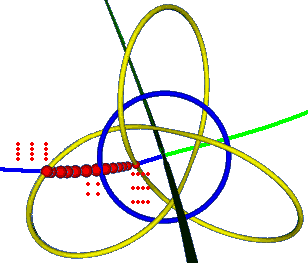
我们发现红色部分上的点对应任意长宽比、两边平行于实轴、虚轴的所有矩形。如果我们旋转它们,就能得到所有矩形的集合。还记得旋转后的轨迹是三叶结吗?这些点旋转得到的无穷多三叶结的并集我们得到了一张新的三叶结的Seifert曲面(下图紫色)——这是所有矩形格子的集合——它像莫比乌斯带那样也是单侧曲面,只不过是把纸条扭转一圈半粘起来!(莫比乌斯带是半圈)
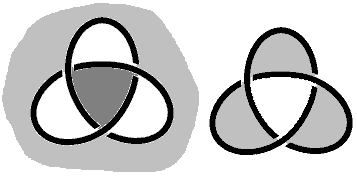
双曲空间中的测地线
最后我们来看格子空间的另外一个表示方法:不仅舍弃关注格子的大小,连格子方向也不管(比如认为所有正方形格子都一样)我们有另一种可视化的方法:用复数$\tau = w_2/w_1$来表示一个格子。但我们交换$w_2$、$w_1$的位置得到$1/\tau = w_1/w_2$也是一个$\tau$的取值,但它们两个值只有一个落在上半平面($Im(\tau)>0$)中。所以这里加上限制:我们今后只在上半平面中讨论。但复数$w_2$、$w_1$有无穷多种取法,所以我们会得到无穷多的$\tau$的值,但我们一般始终能在区域$|Re(\tau)|\le\frac12,|\tau|\ge 1$中找到一个唯一的$\tau$值,我们称这个区域为基本区域(fundamental domain)。其他区域的点与这个区域的点差在哪?它们的$w_1$、$w_2$选取时相差了模矩阵——行列式为1的二阶整数矩阵。反映到复数$\tau = w_2/w_1$上来,它们相差了一些莫比乌斯矩阵(和莫比乌斯带没一点关系)。具体细节见介绍它的PDF。比如$\Delta=0$的无限扁格子在$\tau=+i\infty$处,正方形格子在$\tau=i$处,正六边形格子在$\tau=r=1/2+i\sqrt 3/2$处。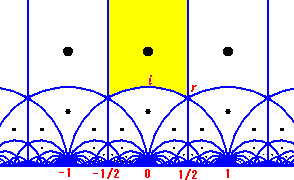
模动力系统反映到$\tau$的上半平面中都是一些圆心在实数轴上的圆弧。我们可以认为这是一个弯曲的二维空间:你看到的圆心在实数轴上的所有圆弧都是“直线”,只是弯曲的二维空间给你造成的错觉——因为我们所在的平直空间无法完美地表达出弯曲的二维空间,就像我们用球极投影画球面上的东西一样图象是扭曲的;这个弯曲的二维空间里面每一个曲边三角形都是一样大的,实轴附近的三角形看上去很小也是弯曲给你造成的错觉——这就是双曲空间!这些“直线”我们叫“测地线”(数学影片《混沌》中讲过测地线)。双曲空间不满足“过直线外一点只能做一条平行线”,它能做无数条平行线!什么是平行?在二维中不相交就是平行。你能在上图中找出否定“过直线外一点只能做一条平行线”的例子吗?
双曲空间早在《维度》第2集就出现过了:
注意到那个圆盘和墙上的图形没?那是埃舍尔从双曲空间的几何学中获得灵感的作品。我们以后将详细讲双曲空间。