洛伦兹和模动力系统: 一个形象可视化的介绍

1.简介

有时，看似不相关的对象居然是相关的......我们想在这里提出一个数学例子，展示分别来自数论和气象的两个动力系统之间的密切联系。

1801年，卡尔·弗里德里希·高斯出版了他的第一个杰作《算数探索》。它涉及到了很多领域的基础理论。今天，这些理论有许多重要方面的应用，比如动力系统作用于格的空间：模动力系统 1963年，气象学家爱德华·罗伦兹正在研究一个非常简单的大气数学模型，他得到了惊人的奇怪吸引子，后来通过著名的蝴蝶效应而广为人知：拍打的翅膀蝴蝶可能会引起大气状态的一些微小的变化就会导致飓风！

我们将会描述这两个数学对象中紧密的拓扑学上的联系。

这篇文章不是一篇严格意义下的数学文章，因为它没包含任何数学证明。我们的主要目的是将涉及到的那些不可思议的数学对象形象化，我们试图在一个比较初级的水平解释更多高深的数学知识，通过图片和影片片段来解释这些知识，这才是该电子文章的主要内容。

我们故事的组织结构很简单：首先，我们会描述Lorenz吸引子 (2.1)和它的模板 (2.2)，然后是格空间 (3.1)、模动力系统 (3.2)和动力系统中的周期轨道 (3.3)，最后我们将在这两个动力系统之间建立起 一个联系 (4.1 和 4.2)

这篇文章是一个数学家和一个几何艺术家共同合作的结果。想了解更多数学方面的知识的读者可以访问 [1]，想欣赏更多图片的读者可以访问[2]

图像由 Ultrafractal [13] 及 Povray [14]制作。绘制纽结所需的图形数据来自Knotplot[12]。更大版本的视频可以在Jos Leys的网站上看到。

注意: 这篇文章包含了大量图片和一些QuickTime影片。装有的Quicktime插件大多数网络浏览器都支持这些影片的播放，影可以通过点击这个 按钮打开，或点击对应的图片链接打开。(我们很抱歉Linux的浏览器例外)

所有影片的最终解释权归 Jos Leys 和 Etienne Ghys所有。

2.洛伦兹动力系统

2.1 洛伦兹动力系统及其周期轨道

这个由E.洛伦兹发现的模型是由下面的三维空间中的微分方程组描述的 [3]：

当洛伦兹在他当时原始的计算机上画出这组微分方程解的轨迹时，他能看到类似右侧（点击图片观看影片）图片： 令人惊讶的事实是，这张照片是强大的。如果我们扰动方程，这种现象仍然存在：轨迹都会趋于接近于一个也就是现在被称为奇怪吸引子的集合。我们不打算在这里讨论与之相关的流体动力学，但洛伦兹吸引子已在现代动力系统成为最典范的象征之一，它是混沌理论的标志。 (例子详见[4])

在二十世纪八十年代，Joan Birman和Bob Williams观察到了一个简单但重要的现象：一个三维向量场中的周期轨道是一个封闭的嵌入曲线，因此定义了一个纽结。他们建议的对这些出现在洛伦茨方程中的拓扑结的研究可能会让我们得到这个重要的动力系统的一些理解[5]。 下图展示了一些可以在洛伦兹动力系统中找到的周期性轨道解。

这些纽结中一些是拓扑学中的平凡结，一些则是非平凡结。比如图中红色轨线就是一个三叶结。Birman和Williams的研究动机之一在于这些周期轨道似乎的确给出了吸引子的一个很好的近似。在右边的图片中(点击播放影片)，我们能够同时看到一组封闭的轨道，这表明洛伦兹吸引子是其所有周期轨道的集合的极限。在某种程度上我们可以认为吸引子是由无数各组成部分的无限条周期性轨道构成的。

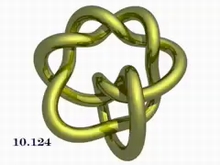
Birman和Williams向我们证实了洛伦兹纽结是很有趣的，里面的内容既丰富又奇怪。比起陈述对于洛伦兹纽结进行数学分析的结果，还不如让我们只关注它的数值描述来得更形象。回想一下，一个纽结就是一个封闭的没有自相交的空间曲线，如果可以在不相交的情况下让一个纽结连续形变成另一个纽结，我们就说说两个纽结是一样的或等价的。 (例子详见[6]， [7]， [8]) 我们可以根据纽结的交点数对纽结进行一种简单的分类，交点数即对给定的纽结的所有投影中最少交点的数目。 比如我们知道交点数在10或10以内的（素）纽结一共有250种。Birman和Williams在研究中发现，这250种纽结中只有8种才能在洛伦兹吸引子中的周期性轨道形成的纽结中找到。

点击下面纽结的图片观看影片(我们通常把纽结编号，比如8.19表示这是最少交点数为8的所有纽结中的第19个，这是一种对纽结进行的传统的而非逻辑性的编号方式)。

在交点数为16或少于16的1 701 936(素) 个纽结当中，只有21个纽结才是洛伦兹动力系统中出现的纽结(使用了计算机和[17]进行检验)。

比如有12个交点数的纽结 "非交错12.725"：

然而八字结是一个反例，它不是洛伦兹纽结。

Back to top

2.2 洛伦兹模板

如何证明这些事实呢？我们想到处理洛伦兹模型的方程将会更容易分析。首先如下图所示构造所谓的洛伦兹模板。

下面我们考虑两个纸带，如影片中所示那样在空间中展开它们。这样就在空间中产生了一个二维的物体，即带有分支的曲面：这就是洛伦兹模板。分支的连接处是中间的图片中看到的垂直线段。如下图所示，这个模板上有一个相当自然的动力系统。

如果我们在这条垂直的线段上定义一个[0,1]的区间,那么每条经过这条线段的轨迹和线段相交的交点坐标记为x当轨迹转一圈后再回到这条垂直的线段上时交点坐标会变成2x mod Z。当我们分析一个周期轨道时，我们可以只分析将这个[0,1]区间映射到自身的"翻倍映射"中的周期点。比如"翻倍映射"将点1/3映射至2/3，然后又会映射回1/3 = 4/3 - 1。所以点1/3是周期为2的周期点，从而我们就得到了模板上的一个周期轨道：先经过模板的一只“耳朵”，然后再经过模板的另一只“耳朵”。图中显示了模板上的一些周期轨道。

事实上，用路径序列来描述这些周期轨道并不困难，即用“左”或“右”两种符号组成一串有限的序列。对任意一个这样的序列，刚好有且仅有一条周期轨道会按照路径序列上的顺序先后经过模板上的左环和右环。反之，一个周期轨道也定义了一个路径序列，最多相差在循环排列中任意选择的起点不同。通过这种方式，你就可以想象数学家们是怎样把路径序列用于洛伦兹结的拓扑学研究了。这就是Birman和Williams所做的工作。Tucker最近建立起了这个用“几何方式描述的洛伦兹吸引子”和原始洛伦兹方程之间更多的联系 [9]，[10]。

Back to top

3. 模动力系统

3.1 格空间及其拓补结构

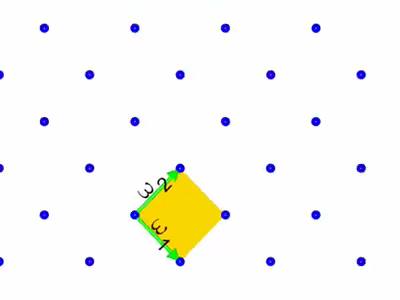
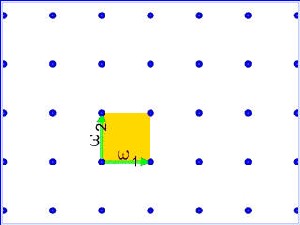
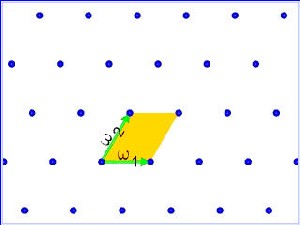
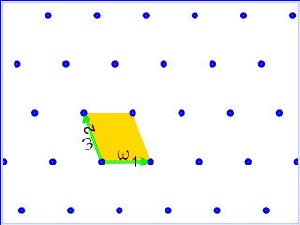
给定两个平面中线性无关的向量ω₁ 、 ω₂， 考虑它们生成的在R²中的子集 L：

L= {n₁ω₁ + n₂ω₂| n₁ , n₂   Z}.

形如这样的平面中的子集我们称作格（子）。值得注意的是，相同的格子L可以由很多不同的一对向量来生成。若a、b、c、d 都是整数，且满足ad−bc= ±1，向量aω₁+ bω₂ 和cω₁+ dω₂将生成同一个格子。

所有格子组成的集合是一个拓补空间：如果两个格子可以由平面中靠得很近的两个向量生成，我们就说这两个格子之间是靠得很近的。伟大的数学家高斯在他的《算数探索》(1801)书中就开始研究这个空间，他深入讨论了整数二次型中的算数理论，后来很多数学家又对此研究了多年。

让我们把平面R²看成复平面C。对于每个格子L，定义两个复数

     ;       .

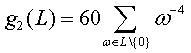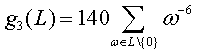很容易验证式中的指数（4和6）只要大于2，这些级数就是收敛的。由于格子是明显关于原点对称的，所以若把指数取成奇数将导致求和的结果为0，因此指数取四次和六次是我们必须首先考虑的。至于系数60和140只是归一化的常数，我们可以不关注它们。下面一个很重要的结论就是，复数对( g₂(L) , g₃(L) )可以完全描述一个格子。更准确地说，(g₂, g₃)和一个格子相对应，当且仅当所谓的判别式 Δ = g₂³− 27g₃²不等于0。 证明详见[11], [16]。

综上所述，所有格子构成的空间可以定义为曲线 Δ = 0 在C²中的补集。

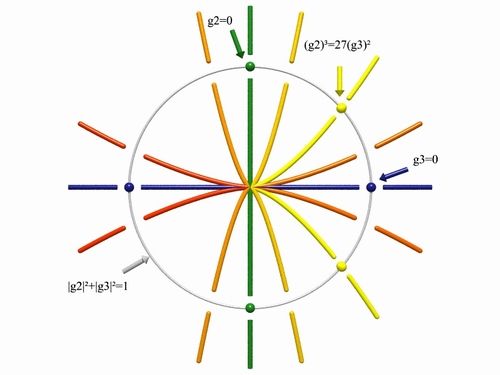左图象征性地展示了复二维空间C²。要注意的是，C² 其实就是R⁴所以这其实是一个四维空间中的图像！水平的蓝色轴代表的是 g₃=0 对应的格子；这条轴相当于是一个复平面C=R²。垂直的绿色轴代表 g₂=0；这是另一个复平面C=R²。黄色曲线代表Δ=0，但这只是复数域中的一维曲线，从实数的角度来看其实是一张曲面。

怎样才能用一种具体的方式来观察这个四维空间中的物体？如果L一个格子，k是一个非零实数，我们可以研究和L完全相同的，仅仅相差一个缩放倍数k的格子kL。因此我们只需要研究那些基本区域面积为1的格子，换句话说就是研究生成格子的两个向量ω₁、ω₂形成的平行四边形的面积为1的格子。注意到

g₂(kL) = k⁻⁴g₂ (L)   ；    g₃(kL) = k^{− 6}g₃(L)，

所以对于每个格子L都能找到唯一的一个k > 0 使得   |g₂(kL)|²+ |g₃(kL)|²= 1.

这就表明，如果我们想研究除去缩放系数过后的格子，或研究基本区域面积为1的格子，我们就得研究Δ为0的集合在单位球面 |g2|2+ |g3|2= 1 上的补集。这个单位球面是三维的，Δ为0的集合与之相交会得到一个一维的交集，它是一个三叶结。比起复二维空间C2，三维球面更容易可视化：如果在球面上选一个点，我们可以从那一点向它的对径点的切空间做投影：这就是球极投影下面的图片显示了二维时的球极投影的情景 (黎曼球面)。 (点击图片观看影片)

既然定义为一个三叶结在三维球面中的补集，所以当我们去掉一个点后这个空间就变成了一个三叶结在普通三维空间中的补集。我们终于可以在这个空间中看到一些有趣的东西了。

这幅图(点击图片观看影片)展示了一个三维球面，确切地说是它在三维空间中的球极投影，或更确切地说这只是那个球极投影在你的二维屏幕上的投影。在影片中球面上的投影点在连续变化，所以你能够看到整个三维球面的样子。蓝色(绿色)的圆圈代表坐标轴 g2=0 (g3 =0)和球面的交线。当投影点一次次经过而落在圆周上时，圆周将被投影成直线。而黄色的三叶结是Δ为0的集合与球面的交线。

让我们看一看一些在基本区域面积为1的格子空间中的额外的结构来更好地了解它的拓扑学。

给定一个格子L和一个角度θ ∈ [0,π]，我们可以将格子在平面中旋转θ角得到另一个格子Lθ。当 θ从0变化到π时就得到了一个格子空间中的圆周。 通常来说，只要θ ≠ 0， 格子L和格子Lθ就是不同的，但这里有两个反例。如果L正方形的格式，它会和它的旋转了π/2后的像重合；如果L是一个正六边形的格子，它会和它的旋转了π/3和2π/3后的像重合。这些事实都表明基本区域面积为1的格子空间中充满了这些旋转产生的圆周。但这些圆周只是拓扑学上的圆周，它们其实都是三叶结，但我们前面提到的两个特殊情况除外：它们在转过π/2和π/3而不是π后就闭合了，所以它们比其他轨道更短，其实这两个轨道就是我们之前就遇到过的蓝色和绿色圆圈。这种将一个三维球面分解成一族三叶结和两个圆周的方法是Seifert纤维化的一个例子。见右图(点击图片观看影片)：

三维球面上还有一个额外的结构可以说是Seifert纤维丛的对偶。我们知道每一个格子都对应一个非零的复数Δ，如果将一个格子乘上一个大于0的实数k，它对应的Δ就相当于乘以了k−12，所以乘上一个缩放因子不会改变Δ的幅角。这就提醒了我们可以通过复数Δ的幅角来分解基本区域面积为1的格子空间。所有有着给定幅角的Δ的格子的集合在三维空间中定义了一个以三叶结为边界的曲面。左图(点击图片观看影片)显示了其中的一个Seifert曲面。

给定一个Δ的幅角值我们就能得到一个曲面。如果把幅角的值取遍，对应的Seifert曲面就将扫过整个三维空间，并且一直保持着同一个三叶结边界。某些幅角的取值会让Seifert曲面刚好经过球极投影的极点，所以在那一刻曲面感觉像是无限大的。(点击图片)

为了理解这个除去一个三叶结后的纤维丛让我们删掉Seifert曲面的一部分而只看三叶结周围的运动情形。下面的影片就展示了对应着四个幅角值的四个Seifert曲面的一部分绕着三叶结转动的情形。拓扑学家说三维球面就是一本打开的书，三叶结就是书的装订轴，Seifert曲面就是书中的一张一张页面。 (点击图片观看影片)

为了显得更有趣一些，让我们看一看现在的全景：让三叶结、轴、Seifert纤维和Seifert曲面一起出现！(点击图片观看影片)

Back to top

3.2 模动力系统

既然我们已经很清楚地了解了基本区域面积为1的格子空间的拓部结构，我们下面就开始在这个空间中定义动力系统。定义非常简单：对每个实数t，考虑矩阵

。

如果L是基本区域面积为1的格子，它在矩阵作用下的像依然是基本区域面积为1的格子。这样我们就定义了一个在基本区域面积为1的格子空间上的动力系统，叫做模动力系统。格子L的轨迹是当时间t为实数时在格子空间中描述的曲线。

我们的目的是给出一个这个动力系统及其周期轨道的一个可视化的描述。这个动力系统是Anosov动力系统中的一个著名的例子，即里面存在着稳定和不稳定的方向。让我们引入另外两个动力系统来解释它：

   ;   .

注意，所以对于两个格子L和  (L和 )来说，如果我们在模动力系统中看它们的将来(过去)，即观察它们被t为正(为负)时作用的像，这两个格子的轨迹将会呈指数级的速度相互趋近。我们说L和 ( )在相同的稳定(不稳定)曲线上。

下图解释了这个情形。首先我们看到了一个初始点L与两条在稳定和不稳定流形中的弧线，即两段s在[−1 , 1]中取某些值对应的 和形成的区间。当模动力系统随时间向前演化推进时我们可以看到，从这些点出发的所有轨迹生成了两张曲面。绿色的曲面对应着稳定流形，可以看到稳定流形很快与中心轨道靠近，之后近得再也无法区分。红色曲面代表不稳定流形，相反它会在空间中膨胀而形成巨大的像降落伞一样的曲面。如果我们继续一直让动力系统向前推进，这个红色的曲面将变得越来越大，会将空间填充得越来越密让我们什么也看不到。最终，影片停止了，模动力系统改为向过去推进，其中也有相似的现象，只不过红色和绿色的角色交换了。这种稳定和不稳定流形的结构在相空间中产生错综复杂的网络成为了研究动力系统的中心工具：即所谓的双曲理论。

Back to top

3.3 周期性轨道及其与三叶结的缠绕

我们现在可以对模动力系统中的周期轨道进行拓扑学上的描述，方法很简单。考虑一个由整数构成的行列式为1的2 × 2的矩阵A ：

_。

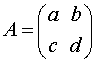很显然矩阵A作用在R²中正方形的格子Z²上是不变的。假设A是双曲的，即 |a + d| > 2，这时A可以在实数范围内对角化。在这种情况下我们就能找到一个2×2的矩阵P使得对于某些t

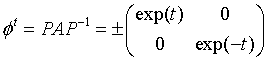
因此每一个双曲矩阵A 定义了模动力系统中的一个周期轨道。

下面的影片片段(点击播放)演示了一个基本区域面积为1的格子空间中的周期轨道。其中每一个点沿着在平面中决定的双曲线运动，这些点的运动轨迹是没有周期的，但作为平面中的一部分的格子的轨迹确实是有周期的。

我们不难发现将A替换成± BAB⁻¹其中B是另一个行列式为1的整数矩阵，我们能得到相同的周期轨道。

在模动力系统中的周期轨道和行列式为1的双曲整数矩阵的共轭类之间存在着自然地双射。

这些周期轨道具有很古老的数学传统意义。我们可以在很多领域中找到它们的不同的形式：模曲面上的闭合测地线、整数不定二次型中的等价类、二次数域中的理想类、连分数等。

每个周期轨道在基本区域面积为1的格子空间中都是一条闭合曲线，因而就在三叶结的补集中定义了一个纽结。我们想通过拓扑学的角度来了解这些模纽结。让我们先来看一些例子。

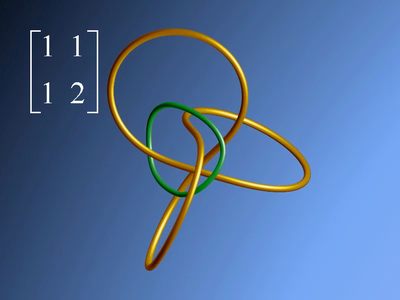矩阵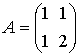所对应的纽结看上去很令人失望，它只是个很小的平凡结. . . 矩阵 对应的纽结仍然是平凡的，但和三叶结的位置关系不同了。而矩阵 对应的纽结就显得更有趣了，它是个三叶结。矩阵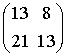 对应的纽结是一个环面纽结 T(4, 5)，而矩阵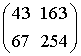和 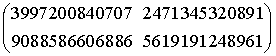对应的纽结就更复杂了！

在我们继续讨论这些纽结的自然状态之前，让我们先问一个看似简单的问题：

一个行列式为1的双曲整数矩阵A所对应的纽结记作 k_A 。能找到一种方法计算 k_A和三叶结之间的缠绕数吗？

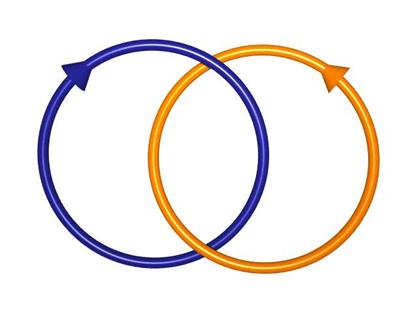
我们需要很快提及三维空间中两个不相交的定向纽结间的缠绕数的概念 (这也是最初由高斯用一种电磁学中很不同的方式提出来的)。 假设两个定向的纽结k₁ (蓝色)和k₂ (橙色)没有相交，选取一个一般的方向投影到平面上，它们的投影当然绝对会相交。

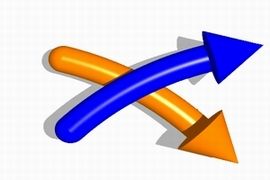
让我们关注蓝色的结k1的投影从上方经过橙色的结k2的投影的交点。如左图所示，这些交点的局部性态有两种。

我们给左边的情况标记为+1，右边的情况标记为−，然后把像这样的所有k₁从k₂上方经过的交点的标记值相加得到的结果就叫做缠绕数。比如左图中蓝色的曲线从上方经过了橙色曲线一次，标记为“+1”，所以缠绕数就是“+1”。在右图中存在着两个带有不同符号标记的从上方经过的交点，所以缠绕数为0。

重要的是，用两个纽结任意方向上的投影来计算缠绕数我们都能得到相同的结果，且两个纽结在不穿过对方的情况下连续形变都不会改变计算的结果，这就是所谓的不变量。

现在让我们回到刚才提的那个问题上，尝试求出k_A和三叶结之间的缠绕数。让我们回忆一下，这个三叶结是Δ的幅角取某个定值对应的Seifert曲面的边界，比如幅角取0(代表Δ是一个正实数)。在三叶结对整个空间的补集里给定一个闭合的定向曲线 我们可以观察它在Δ映射下的像：一条复平面中的不过原点的闭合曲线。显然，曲线和三叶结之间的缠绕数就是这条闭曲线关于原点的指数，即曲线绕原点的圈数。计算这个指数的一种方法是通过在代数上计算曲线和实轴的交点，若曲线从下半平面到上半平面就记为“1+”，反之记为“−1”。 从拓扑学的角度来看，这表明了Seifert曲面是双面曲面，我们可以在代数上计算k_A和Seifert曲面的交点。

下图描述了上述情景。给定一个矩阵A，我们可以同时画出纽结k_A和Seifert曲面。当动力系统演化时，k_A 上的点会一次又一次从正侧或负侧穿过Seifert曲面，记为“1+”和“−1”。我们要求的缠绕数就等于这些标记的和。在第一个例子中对应两个正向的标记，第二个例子中第一个为正，第二个为正，第三个为负。

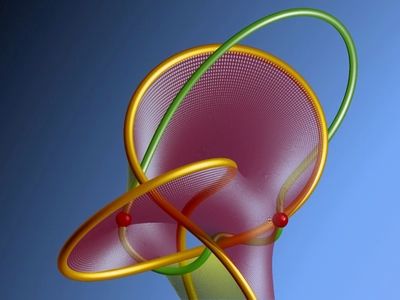其实我们有一个和著名的算术函数相关的很好的公式来计算缠绕数。

我们给出两个矩阵：

U=  ;  V=  .

结果表明，任何行列式为1的整数矩阵A都是共轭的，即能够写成一系列U’和V’的乘积。如

A= 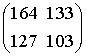= UVVVUUVVVUUUUV

U和V组成的序列定义了一个唯一的循环排列。对于每个矩阵A，定义R(A)是乘积中因子U的个数减去乘积中因子V的个数。这个关于矩阵A的不变量叫A的Rademacher不变量。下面是 [1]中的结论：

定理: k_A 和三叶结之间的缠绕数等于矩阵A的Rademacher不变量。

我们只能在 [1] 中提供一些证明和更多的信息，在下一节我们还将给出一些解释。

Back to top

4 洛伦兹和模纽结

4.1 模模板

我们前面已经讨论了洛伦兹吸引子中的周期轨道，即洛伦兹纽结和模动力系统中的周期轨道模纽结.

定理：洛伦兹纽结和模纽结是相同的。

更准确地说，对每一个模纽结k_A，我们都能将它在三维空间中变形，使它和一个洛伦兹吸引子中的周期轨道相同，反之也成立。不幸的是，我们无法在这里提供证明，我们会用图片和影片把变形的过程展示出来

证明中的第一步包括在基本区域面积为1的格子空间构造了一个像洛伦兹模板一样的模模板。首先从构造由两个部分组成的一维物体开始： 第一个部分是基本区域面积为1的格子空间中的所有六边形格子的空间对应的那个圆周，即我们前面描述格子空间时描述的那两条轴中的一条，第二个组成部分是所有基本区域是有着从π/3到2π/3的内角的水平的菱形格子的集合。 换句话说，就是由两个关于x轴对称的夹角在π/3与2π/3之间的向量生成的格子的集合 (向量围成的平行四边形面积为1)。当角度变化时就产生了一个区间[π/3, 2π/3]。当夹角等于π/3或2π/3时对应的的格子刚好是六边形的格子，所以这个区间会把六边形格子对应的那个圆周的两个点连起来。其实那个区间就是圆的直径。(点击右图观看影片)

右图展示了这部分的构造。我们先将三叶结做了两次旋转(一次在四维空间中旋转，另一次在三维空间中)，放在一个看起来舒服的位置上，然后画出了刚才讨论的圆周和它的直径。(点击图片)

然后我们把这个一维物体沿着不稳定的方向扩大成一个二维的模板。要描述清楚这个过程还存在着技术上的很多细节问题，我们只需要关注影片中的模板是怎样慢慢建立起来的即可。值得注意的是我们在讨论的是拓扑学，所以这个构造绝对不是唯一的，我们只是为了直观而选择了一种特别的方式。

现在下一个目标就是把模纽结不穿过三叶结而连续形变到模板上，形变之后的纽结就会像洛伦兹纽结那样全都刚好落在模板上。我们同样不能提供证明，详见[1]。总的思路就是用一种很古老的方法(又是高斯想出来的)将整个基本区域面积为1的格子空间压缩至那个一维物体的一个很小的邻域中：给定一个格子L，一定在L中存在一个非零的最短的向量v，除非这个格子的基本区域的形状是菱形的，这个向量就是唯一的。再找一个和v不共线的向量w。向量v、w就是一组特别选择的生成L的基。现在我们在保持平行四边形面积为1的情况下把向量w的长度逐渐缩小，同时逐渐增加v的长度，直到它们落到模板上为止。让我们不要拘泥于着其中的细节问题，看看这些图像中的纽结是怎样形变到洛伦兹纽结的位置上去的。

Back to top

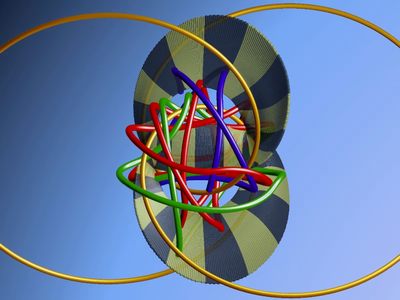4.2 最后的两个讨论

最后的评论 我们知道洛伦兹方程中的周期轨道可以被一串又有限的“左”和“右”组成的符号编号，它表示的是路径经过洛伦兹吸引子“左耳朵”和“右耳朵”的先后顺序。我们可以验证和一条周期轨道对应的矩阵A分解后的的乘积表达式中U和V出现的顺序代表着像“左”和“右”那样的同样的顺序。所以上面说到的变形就会把洛伦兹纽结和k_A对应起来。走左耳朵的路径就对应着与三叶结的缠绕数+1的那种情况，走右耳朵则对应缠绕数−1的情况。

由此我们得出结论k_A和三叶结的缠绕数等于在A的乘积表达式中字母U出现的次数减去字母V出现的次数。这就是一种证明我们提到过的那个定理的一个方法之一：A和三叶结的缠绕数是Rademacher’数。

最后的探讨 模动力系统并不是唯一一个值得在基本区域面积为1的格子空间中讨论的动力系统。我们还可以讨论由前面我们知道代表稳定流形的矩阵定义的动力系统。这个动力系统通常叫horocyclic动力系统。 我们需要很多的图片来展示这个动力系统的精彩方面，但我们现在只把注意力放在一个方面：它的周期性轨道上。给定实数t和s，我们考虑由两个复数 exp(t) 和 s.exp(t) + i exp(−t)生成的格子L_s,t 。固定t不变，让s从0取到1，我们就在基本区域面积为1的格子空间中能得到一条周期曲线c_t ，即的一条周期轨道。下面的影片显示了当t在某个区间中变化时c_t的变化。当t是一个很大的负数时，曲线c _t是一个三叶结上很小的平凡的圆圈。当t为很大的正数时曲线c_t将会变得越来越长，最后将把整个空间填满。

我们现在知道c_t曲线簇会趋于将整个空间以均匀的方式填满，但对这个现象的填充速度的定量估计等价于数学中最迷人的问题之一——著名的黎曼猜想！[15]

Back to top

参阅

[1] GHYS, E.: Knots and Dynamics, to appear in the proceedings of the International Congress of Mathematicians, Madrid 2006.

[2] LEYS, J.: Mathematical Imagery. http://www.josleys.com